概要
最小二乗法を用いて順番に並んだ4つ以上の点を3次Bezierを用いて曲線あてはめをしてみます。
結果
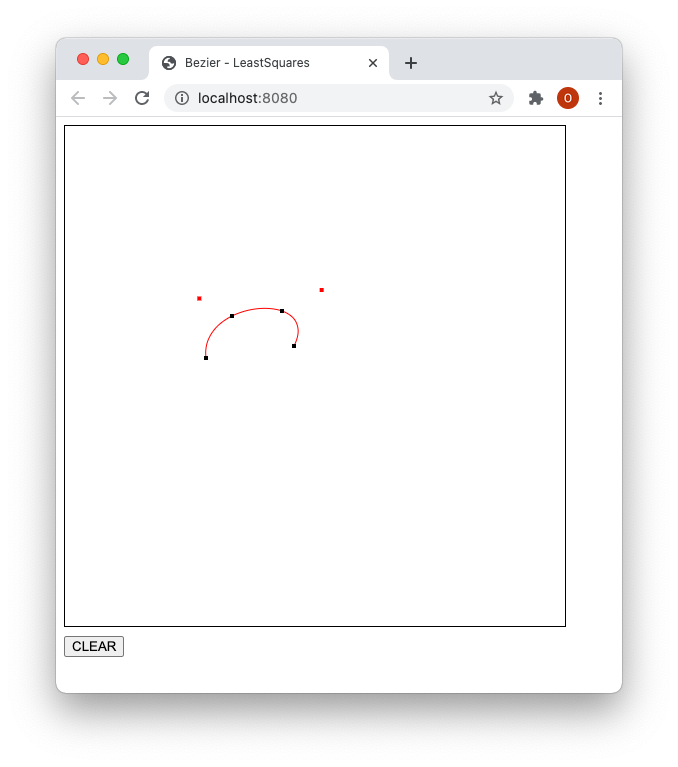
黒い点はクリックした点、赤い点は求められた3次Bezierのコントロールポイントです。
- 4点を指定したところ
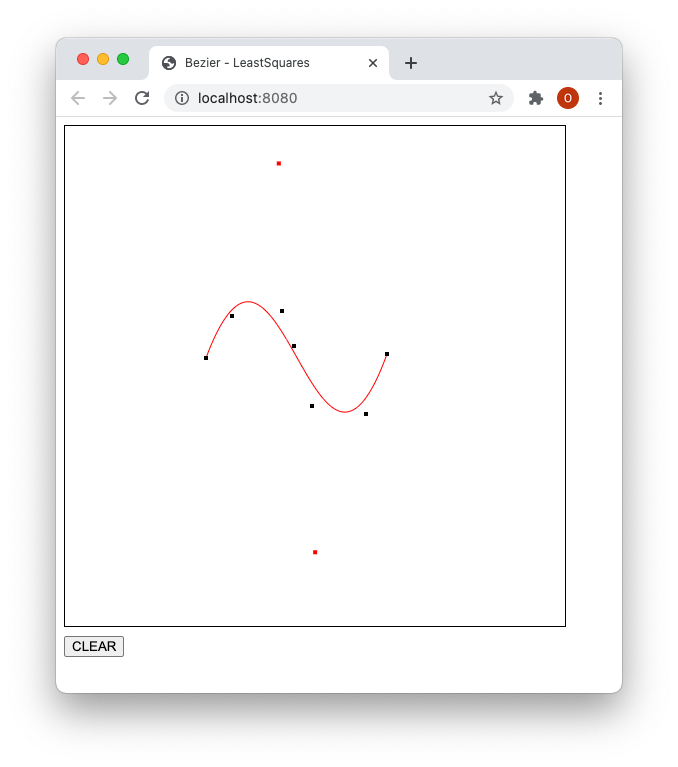
- 7点を指定したところ
プログラム
export default
_ => {
const l = _.length - 1
const s = _[ 0 ]
const e = _[ l ]
let pp = 0, pq = 0, qp = 0, qq = 0, p = 0, q = 0
for ( let $ = 1; $ < l; $++ ) { // Bypass first and last element, because 't' or 'u' will be zero.
const t = $ / l
const u = 1 - t
const P = 3 * u * u * t
const Q = 3 * u * t * t
pp += P * P
qq += Q * Q
const PQ = P * Q
pq += PQ
qp += PQ
const R = _[ $ ] - u * u * u * s - t * t * t * e
p += P * R
q += Q * R
}
const dm = pp * qq - pq * qp
return [
+ p * qq / dm - q * pq / dm
, - p * qp / dm + q * pp / dm
]
}
<!DOCTYPE html>
<html lang=zxx>
<title>Bezier - LeastSquares</title>
<div>CLICK 4 or more points please.</div>
<canvas id=Canvas width=500 height=500 style="border: 1px solid black"></canvas>
<br>
<button id=Clear>CLEAR</button>
<script type=module>
const
C2D = Canvas.getContext( '2d' )
const
Dot = ( x, y ) => C2D.fillRect( x -2, y - 2, 4, 4 )
import CurveFit from './NPM/index.js'
// import CurveFit from './node_modules/@satachito/curve_fit/index.js'
// npx web-dev-server --node-resolve --open
// With web-dev-server node resolver:
// import CurveFit from '@satachito/curve_fit'
const
$ = []
const
Draw = () => {
C2D.clearRect( 0, 0, Canvas.width, Canvas.height )
if ( $.length > 3 ) {
C2D.beginPath()
C2D.moveTo( ...$[ 0 ] )
const [ xP, xQ ] = CurveFit( $.map( _ => _[ 0 ] ) )
const [ yP, yQ ] = CurveFit( $.map( _ => _[ 1 ] ) )
C2D.bezierCurveTo( xP, yP, xQ, yQ, ...$[ $.length - 1 ] )
C2D.strokeStyle = 'red'
C2D.stroke()
C2D.fillStyle = 'red'
Dot( xP, yP )
Dot( xQ, yQ )
}
C2D.fillStyle = 'black'
$.forEach( _ => Dot( ..._ ) )
}
Clear.onclick = () => ( $.length = 0, Draw() )
Canvas.onclick = ev => ( $.push( [ ev.offsetX, ev.offsetY ] ), Draw() )
</script>
解説
まずは2次元で考えます。
-
始点を $(s_x,s_y)$
-
制御点1を $(p_x,p_y)$
-
制御点2を $(q_x,q_y)$
-
終点を $(e_x,e_y)$
とする2次元の3次ベジエ曲線は媒介変数をtとする以下の式で表されます。
\left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} (1-t)^3s_x+3(1-t)^2t p_x + 3(1-t)t^2 q_x+t^3e_x \\ (1-t)^3s_y+3(1-t)^2t p_y+3(1-t)t^2 q_y+t^3e_y \end{array} \right],\; t=0…1
以下のような関数を用意すると
bz(t,s,p,q,e)=(1-t)^3s+3(1-t)^2t p + 3(1-t)t^2 q+t^3e
このようにも書けます。
\left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} bz(t,s_x,p_x,q_x,e_x) \\ bz(t,s_y,p_y,q_y,e_y) \end{array} \right],\; t=0…1
最小二乗法で求めるわけですからまずこれの誤差関数を求めてみましょう。
まず4点がクリックされた場合を考えてみます。4点をクリックされた順にcs, c1, c2, ceとします。計算で2つの点d1,d2を求めると誤差は以下のように考えられます。
||\vec{c_1d_1}||+||\vec{c_2d_2}||
最小二乗法では誤差の大小だけが重要になるので、扱いやすくするためにこれを二乗して2で割ります。以下のようになります。
\frac{{(d1_x-c1_x)}^{2} + {(d1_y-c1_y)}^{2} + {(d2_x-c2_x)}^{2} + {(d2_y-c2_y)}^{2}}{2}
d1, d2 を求めるにはtを以下のようにして3次ベジエの式にあてはめます。
t = \frac {1}{3}\ ,\frac {2}{3}\
tの決め方は他にもありますが、だいたいこれで十分な結果が出ます。
n点クリックされた場合に一般化しましょう。
J = \sum_{i=1}^{n-2}\frac 1{2}(bz(\frac i{n-1},s_x,p_x,q_x,e_x)-ci_x)^2+\sum_{i=1}^{n-2}\frac 1{2}(bz(\frac i{n-1},s_y,p_y,q_y,e_y)-ci_y)^2
Σの中をpx,qx,py,qyについて微分します。px,qx と py,qy は排他なので、結局関数bzとciについて微分すればよいです。
(bz(t,s,p,q,e)-c)^2
u を ( 1 - t )としてbzを展開すると
Diff(c,t,s,p,q,e) = (u^3s+3u^2t p+3ut^2q+t^3e-c)^2
ここで
A=u^3s,B=3u^2t,C=3ut^2,D=t^3e,E=-c
とおくと
Diff(c,t,s,p,q,e) = (A + Bp + Cq + D + E)^2
\\
= B^2p^2 + C^2q^2 + 2BCpq +
\\ 2ABp + 2ACq + 2BDp + 2BEp + 2CDq + 2CEq +
\\ A^2 + D^2 + E^2 + 2AD + 2AE + 2DE
pとqで偏微分します。ついでに2で割っておきます。
\frac{\partial Diff}{2\partial p}=B^2p + BCq + AB + BD + BE
\\
\frac{\partial Diff}{2\partial q}=BCp + C^2q + AC + CD + CE
A,B,C,D,Eを戻すと
\frac{\partial Diff}{2\partial p}
=9u^4t^2p + 9u^3t^3q + 3u^5ts + 3u^2t^4e - 3u^2tc
\\=(3u^2t)( 3u^2tp + 3ut^2q + u^3s + t^3e - c )
\\
\\
\frac{\partial Diff}{2\partial q}
=9u^3t^3p + 9u^2t^4q + 3u^4t^2s + 3ut^5e - 3ut^2c
\\=(3ut^2)( 3u^2tp + 3ut^2q + u^3s + t^3e - c )
最後にΣの分だけ係数を足し込んでp,qについて連立方程式をといて返しています。
最後に
npm のパッケージにしておきました。
3次元にしたい場合は、単にz座標についてBezierCPsを呼べばいいはずです。
3次ベジエ曲線のあてはめをやる場合、接線接続をするために始点か終点あるいは両方のタンジェントを決めたい場合があります。
その場合は
https://github.com/soswow/fit-curve
とかがあります。