ポアソン回帰モデルの使い方

ポアソン回帰

ポアソン回帰は次のように、x軸の値に応じて誤差分布のパラメータが変化するデータをモデル化する際に使います。

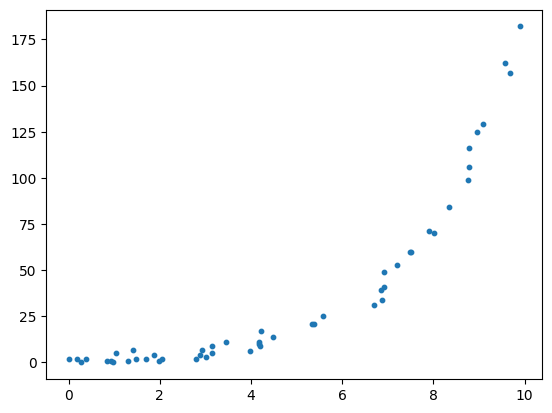
このデータの生成プログラム

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

sample

# 真のパラメータ
true_w0 = 0.3
true_w1 = 0.5

# 人工データ（観測データ）
#乱数生成の初期化をしてからxに代入
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
#計算した平均値μを持つポアソン分布から乱数を生成し、目的変数yに代入
y = stats.poisson(mu = np.exp(true_w0 + true_w1 * x)).rvs()

plt.scatter(x, y, s=10)

回帰

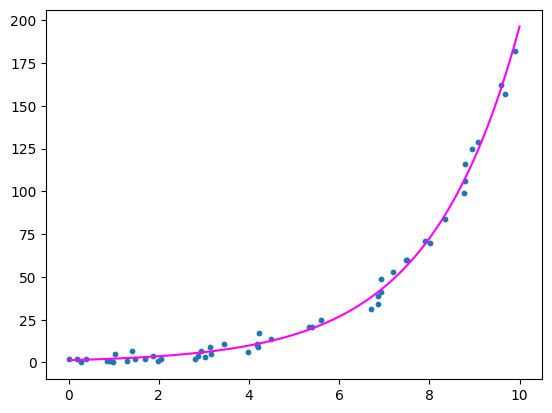
リンク関数を対数関数（y=log(x)）（つまり，逆リンク関数を指数関数(y=exp(x))）に設定した場合のポアソン回帰モデルを作ります。

sample.py

# scikit-learnのTweedieRegressorクラスからインスタンスを呼び出す
model = TweedieRegressor(fit_intercept=True, power=1, link='log')

# 過去のデータを最もよく説明する最適なパラメータを探索
# y = w0 + w1x  の w0～w1 を算出
model.fit(x[:, np.newaxis], y)

# モデルが推定したパラメータ値を確認
# 切片(バイアス)　w0
print(model.intercept_)
# 係数パラメータ　w1
print(model.coef_)

# 最適なパラメータを使って出力の予測値を生成
xfit = np.linspace(0, 10, 1000)
yfit = model.predict(xfit[:, np.newaxis])

plt.scatter(x, y, s=10)
plt.plot(xfit, yfit, color='magenta')

結果

真のパラメータに近い値を出せています。

ここまで読んでくださりありがとうございました！