量子情報理論の基本：量子誤り訂正（スタビライザー符号：２） #量子コンピュータ

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

はじめに

前回の記事で、スタビライザーに関する基礎知識とスタビライザーが意味あるものとして成り立つための条件について学びました。一言で復習すると、スタビライザー群が有意味であるためには、その要素に$-I$が含まれていないことに加え、生成元たちが可換であるということが必要十分な条件であり、独立な生成元の個数が$n-k$個だとすると、スタビライズされる部分空間は$2^k$次元になります、ということでした。今回の記事では、スタビライザーの動的な側面に注目します。量子情報理論において量子状態の変化は、ヒルベルト空間上で定義された状態ベクトルに対するユニタリ変換として通常記述されますが、スタビライザーを使った記述の仕方（スタイライザー形式）もあります。今回は、その説明をします。またしてもスタビライザー符号の話にまで至りませんが、スタビライザー形式を用いた誤り訂正を理解するには必須の知識になりますので丁寧に刻みます¹。さらに、この形式を使うと、量子計算が古典計算機でシミュレーション可能であるための条件が明らかになります。「Gottesman-Knillの定理」という有名な定理がありますので、その説明をします。

参考にさせていただいたのは、以下の文献です。

スタビライザー形式におけるユニタリゲート

本題に入る前に、意味のあるスタビライザー群が満たすべき条件について知っておくべきことがあります。前回の記事で説明しても良かったのですが、省略してしまいました。どんな条件かと言うと、$-I$がスタビライザー群$S$の要素でないとすると、すべての$g \in S$に対して$g^{\dagger}=g$が成り立ちます、ということです。つまり、意味のあるスタビライザー群の要素$g$はエルミートです（かつ、ユニタリです）。それでは、証明してみます²。

【証明】

スタビライザー群$S = <g_1, g_2, \cdots , g_l>$の要素は一般的に、

g = \prod_{i=1}^{l} (g_i)^{r_i}  \tag{1}

と書けます。ここで、$r_i \in \{0,1\}$です（前回の記事の補題１で$g_{i}^{2}=I$となることが示されたので$r_i$は$0$か$1$としておけば良いです）。スタビライザー群の生成元同士は可換か反可換なので、式(1)より$g^{2}$は、$+I$か$-I$になります。$g$はスタビライザー群$S$の要素なので、群の定義より$g^{2}$もスタビライザー群$S$の要素です。前提より、スタビライザー群$S$には$-I$は含まれないので、

g^{2}=I \tag{2}

でなければなりません。$g$はユニタリなので（パウリ演算子の積なので$g^{\dagger}g=I$）、式(2)の両辺に左から$g^{\dagger}$をかけると、

g = g^{\dagger} \tag{3}

となり、$g$はエルミートです。（証明終）

それでは、本題に入ります。

スタビライザー群$S = < g_1, g_2, \cdots , g_l>$によってスタビライズされる状態のことを「スタビライザー状態」と呼び、その状態を要素とする部分空間を$V_s$と書くことにします。スタビライザー状態は量子状態なので、その上で行われる量子計算や量子系の時間変化はユニタリ演算子を適用することで記述できます。最初の状態を$\ket{\psi} \in V_s$、ユニタリ演算子を$U$と書くことにすると、

U \ket{\psi} = U g_i \ket{\psi} = U g_i U^{\dagger} U \ket{\psi}  \tag{4}

とできます。この式をじっと眺めるとわかると思いますが、ユニタリ変換後の状態$U \ket{\psi}$は、$U g_i U^{\dagger}$のような共役作用³をした生成元によってスタビライズされます。つまり、量子系の変化を量子状態の変化と見るのではなく、それをスタビライズする演算子（生成元）の変化と捉えることができるということです。このような記述の仕方のことを「スタビライザー形式」と言います。量子力学における「シュレーデンガー描像」と「ハイゼンベルグ描像」との対比に相当しています⁴。

例えば、初期状態として$\ket{0}^{\otimes n}$を用意して、それをユニタリ変換$U$で表される量子回路を通したとします。これをスタビライザー形式の言葉で言うとどうなるかを考えてみます。初期状態を1つの状態として決めるには、量子ビット数$n$と同じ数の生成元をもったスタビライザー群をもってくる必要がありました（前回の記事参照）。$\ket{0}$をスタビライズするのはパウリ$Z$なので、$\ket{0}^{\otimes n}$をスタビライズするスタビライザー群$S$は、$S = < Z_1, Z_2, \cdots , Z_n >$となります。この生成元は、ユニタリ変換によって、$S^{\prime} = < U Z_1 U^{\dagger}, U Z_2 U^{\dagger}, \cdots , U Z_n U^{\dagger}>$となります。これが、スタビライザー形式の場合の最終状態を表します。つまり、最終量子状態は、$S^{\prime}$でスタビライズされる量子状態になっています。ということです。

これから、スタビライザー形式を使って、いろんな物事を語っていくことになるのですが、それに際し、スタビライザーの生成元を構成するパウリ演算子が、代表的なユニタリゲートでどんな変換をするのかを知っておくのは大事なことです。まずは簡単な1量子ビットのユニタリゲートによって、パウリ演算子がどう変換されるかを表にしてみます。

ユニタリゲート	入力	出力
$H$	$X$	$Z$
	$Z$	$X$
$S$	$X$	$Y$
	$Z$	$Z$
$X$	$X$	$X$
	$Z$	$-Z$
$Y$	$X$	$-X$
	$Z$	$-Z$
$Z$	$X$	$-X$
	$Z$	$Z$

1行目は、入力$X$に対して$H$を演算すると出力は$Z$になるということを表しています。式で書くと、$HXH = Z$ということです。各演算子の行列定義を当てはめてみれば、すぐわかると思います（というか、公式として覚えてますよね）。スタビライザー形式の言葉で言うと、$X$でスタビライズされた状態($\ket{+}$)にアダマール$H$を適用した状態は、$Z$によってスタビライズされた状態($\ket{0}$)になります、ということです。以下同様、この表が成り立っていることは容易に確認できると思います。入力の方に$Y$がないのはなぜ？と思われるかもしれませんが、$Y=iXZ$なので、入力$Y$に対する結果は、$X$と$Z$に対する出力から直ちにわかるからです。例えば、$HYH$は$HYH=iHXYH=iHXH \cdot HZH=iZX=-Y$です。

次に2量子ビットのユニタリゲートの代表例として、制御NOT(CNOT,CX)と制御Z(CZ)に対する変換を見てみます。

ユニタリゲート	入力	出力
$CNOT$	$X_1$	$X_1 \otimes X_2$
	$X_2$	$X_2$
	$Z_1$	$Z_1$
	$Z_2$	$Z_1 \otimes Z_2$
$CZ$	$X_1$	$X_1 \otimes Z_2$
	$X_2$	$Z_1 \otimes X_2$
	$Z_1$	$Z_1$
	$Z_2$	$Z_2$

ここで、各パウリ演算子についている下付き添字は適用する量子ビット番号を表しており、1番目を制御ビット、2番目を標的ビットとしています。これが本当に正しいかどうかは、先程と同様に行列表現で計算してみればわかるのですが、$4 \times 4$の行列計算は少し面倒なので、ここはブラケット記法で計算してみることにします。

CNOTとCZに対応したユニタリ変換を各々$U_{CNOT}$と$U_{CZ}$とすると、

\begin{align}
U_{CNOT} &= \ket{0} \bra{0} \otimes I_2 + \ket{1} \bra{1} \otimes X_2 \\
U_{CZ} &= \ket{0} \bra{0} \otimes I_2 + \ket{1} \bra{1} \otimes Z_2  \tag{5}
\end{align}

と書けるので、例えば、CNOTの1行目は、

\begin{align}
U_{CNOT} (X_1 \otimes I_2) U_{CNOT}^{\dagger} &= (\ket{0} \bra{0} \otimes I_2 + \ket{1} \bra{1} \otimes X_2) (X_1 \otimes I_2) (\ket{0} \bra{0} \otimes I_2 + \ket{1} \bra{1} \otimes X_2) \\
&= \ket{0} \bra{0} X_1 \ket{0} \bra{0} \otimes I_2 + \ket{0} \bra{0} X_1 \ket{1} \bra{1} \otimes X_2 + \ket{1} \bra{1} X_1 \ket{0} \bra{0} \otimes X_2 + \ket{1} \bra{1} X_1 \ket{1} \bra{1} \otimes X_2 X_2 \\
&= \ket{0} \bra{0} X_1 \ket{1} \bra{1} \otimes X_2 + \ket{1} \bra{1} X_1 \ket{0} \bra{0} \otimes X_2 \\
&= \ket{0} \bra{1} \otimes X_2 + \ket{1} \bra{0} \otimes X_2 \\
&= (\ket{0} \bra{1} + \ket{1} \bra{0}) \otimes X_2 \\
&= X_1 \otimes X_2 \tag{6}
\end{align}

となり、確かに正しいです。CZの1行目は、

\begin{align}
U_{CZ} (X_1 \otimes I_2) U_{CZ}^{\dagger} &= (\ket{0} \bra{0} \otimes I_2 + \ket{1} \bra{1} \otimes Z_2) (X_1 \otimes I_2) (\ket{0} \bra{0} \otimes I_2 + \ket{1} \bra{1} \otimes Z_2) \\
&= \ket{0} \bra{0} X_1 \ket{0} \bra{0} \otimes I_2 + \ket{0} \bra{0} X_1 \ket{1} \bra{1} \otimes Z_2 + \ket{1} \bra{1} X_1 \ket{0} \bra{0} \otimes Z_2 + \ket{1} \bra{1} X_1 \ket{1} \bra{1} \otimes Z_2 Z_2 \\
&= \ket{0} \bra{0} X_1 \ket{1} \bra{1} \otimes Z_2 + \ket{1} \bra{1} X_1 \ket{0} \bra{0} \otimes Z_2 \\
&= \ket{0} \bra{1} \otimes Z_2 + \ket{1} \bra{0} \otimes Z_2 \\
&= (\ket{0} \bra{1} + \ket{1} \bra{0}) \otimes Z_2 \\
&= X_1 \otimes Z_2 \tag{7}
\end{align}

となり、これも正しいことが確認できます。他の行も同様にして確認できます。

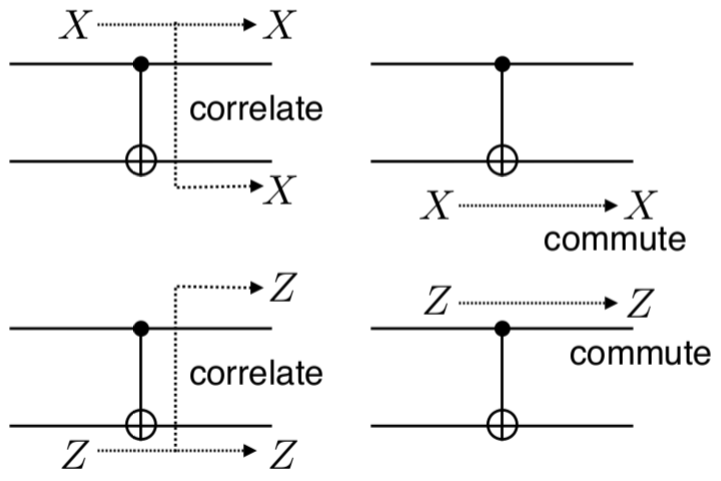
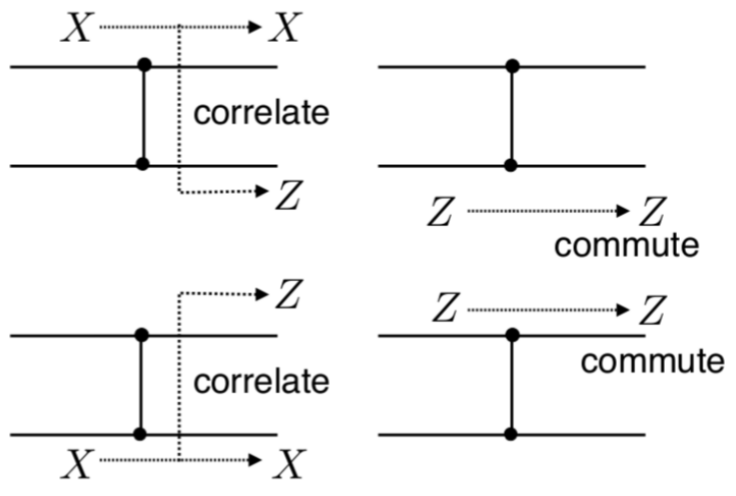
2量子ビットの場合の変換規則は一見わかりにくいですが、覚えるための良い図が、参考文献3にあるので、引用します。

ここで、commuteと書かれているのは可換ということです。CNOTの標的ビットに$X$が入ってきたときの$X$を$X_2$と書くことにすると、$U_{CNOT} X_2 U_{CNOT}^{\dagger} = X_2$となり、$U_{CNOT} X_2 = X_2 U_{CNOT}$なので可換です、ということです（制御ビットにかかる恒等演算子は省略）。その他のcommuteの箇所も見てください。意味はわかりますね。参考文献4に覚え方は「黒丸はZと可換、白丸はXと可換」と書いてありました。確かにその通り、これで覚えると良いです。

一方、correlateと書かれている箇所は相互作用するということです。CNOTの制御ビットに$X$が入ってきたとき、出力側の制御ビットに$X$が現れると同時に標的ビットにも$X$が現れています。制御ビットに入力した影響が標的ビットにも現れるということなので、これは相互作用の効果があった証拠です、という意味だと思っておけば良いです。CNOTの標的ビットに$Z$が入ってきたときも相互作用によって制御ビットにも$Z$が現れます。CNOTの場合、$X$が入ってきたら$X$しか出ない、$Z$が入ってきたら$Z$しか出ないのでわかりやすいですが、CZの場合は違います。が、CZはCNOTの標的側の$X$ゲートをアダマールで挟んだものに等しいということを思い起こしてみれば、わかると思います。

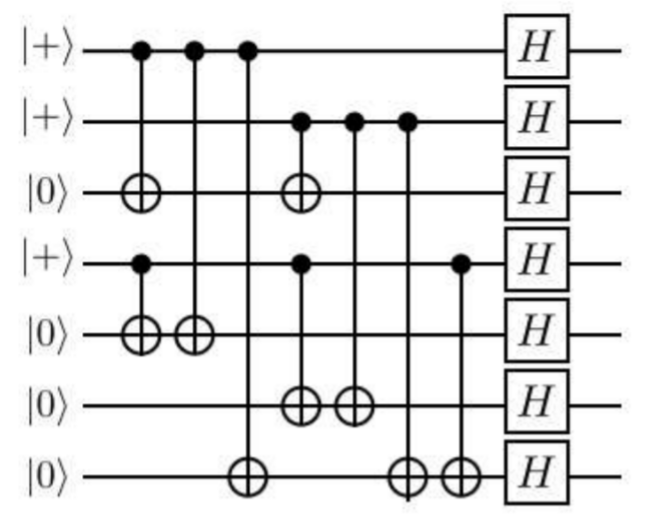
変換規則がわかったところで、具体例で理解を深めてみましょう。例えば、以下の量子回路図があったとします（参考文献3からの引用です）。

この図の初期状態は各量子ビットに$\ket{0}$とか$\ket{+}$が設定されている状態です。この状態をスタビライズするスタビライザー群の生成元は最終的にどうなるでしょうか。

まず、初期状態に対する生成元です。7量子ビットの状態をユニークに規定しないといけないので、7個の生成元が必要です。簡単にわかるように、$\ket{0}$の箇所には$Z$を$\ket{+}$の箇所には$X$を置いて、7個の独立な生成元を作れば良いです。

\begin{align}
S &= < g_{1},g_{2},g_{3},g_{4},g_{5},g_{6},g_{7} > \\
&= < XIIIIII, IXIIIII, IIZIIII, IIIXIII, IIIIZII, IIIIIZI, IIIIIIZ >  \tag{8}
\end{align}

ですね。ここで、テンソル積の記号$\otimes$は省略しました。また、量子ビット番号を表す下付き添字も省略しました。恒等演算子まで省略するとわけがわからなくなるので、$I$は明記するようにしました。

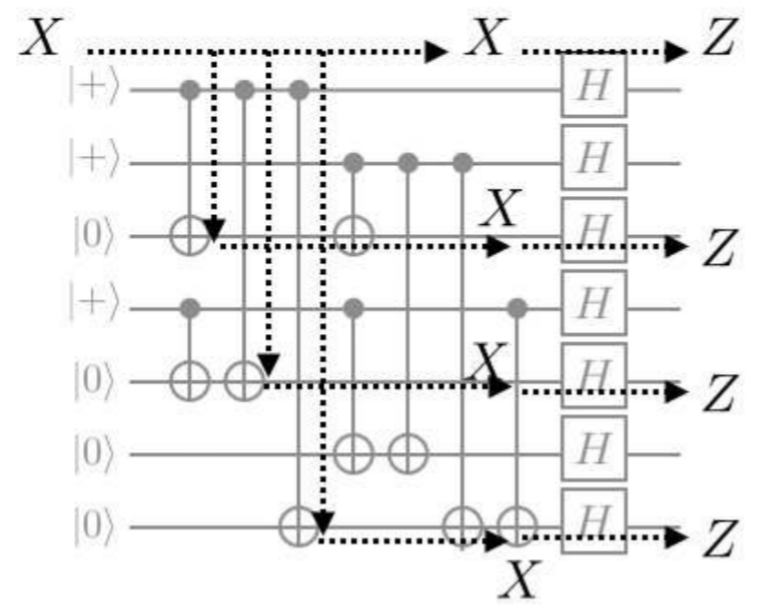
各生成元がこの回路を通してどのように変換されるかを、先程の変換規則を参照しながら追っかけていきます。最初の生成元がどうなるかというと、以下の図のようになります。

1番目の量子ビット以外はすべて恒等演算子なので無視して、1番目の$X$だけに注目すれば良いです。結果は、1番目と3番目と5番目と7番目が$Z$で、残りが$I$となります。すなわち$ZIZIZIZ$です。その他の生成元も同様にやると、結局、最終的な生成元は、

\begin{align}
S^{\prime} &= < g_{1}^{\prime},g_{2}^{\prime},g_{3}^{\prime},g_{4}^{\prime},g_{5}^{\prime},g_{6}^{\prime},g_{7}^{\prime} > \\
&= < ZIZIZIZ, IZZIIZZ, XXXIIII, IIIZZZZ, XIIXXII, IXIXIXI, XXIXIIX >  \tag{9}
\end{align}

となります。最終的な量子状態はどうなるかというと、$\ket{0}^{\otimes 7}$に対して各生成元に対応した固有値+1の射影$(I+g_{i}^{\prime})/2$を順に施せばわかります。そうすると、それがすべての生成元によってスタビライズされるスタビライザー状態になっているはずなので。ということで、やってみます。

\ket{\psi} \rightarrow \ket{\psi^{\prime}} \propto \prod_{i=1}^{7} \frac{I+g_{i}^{\prime}}{2} \ket{0}^{\otimes 7} \tag{10}

となるのですが、ここに登場する射影はすべて可換なので$Z$しか含まない射影を後ろにもっていき、先に$\ket{0}^{\otimes 7}$に演算しても良いです。$Z$しか含まない射影の結果は$\ket{0}^{\otimes 7}$のまま不変になるので、実質$X$を含んでいる射影のみを実行すれば良くて、正規化を考慮すると以下のようになります（地道な計算部分は省略しました）。

\begin{align}
\ket{\psi^{\prime}} = & 4 \frac{I+g_{7}^{\prime}}{2} \frac{I+g_{6}^{\prime}}{2} \frac{I+g_{5}^{\prime}}{2} \frac{I+g_{3}^{\prime}}{2} \ket{0}^{\otimes 7} \\
= & (\ket{0000000}+\ket{1110000}+\ket{1001100}+\ket{0111100} \\
& +\ket{0101010}+\ket{1011010}+\ket{1100110}+\ket{0010110} \\
& +\ket{1101001}+\ket{0011001}+\ket{0100101}+\ket{1010101} \\
& +\ket{1000011}+\ket{0110011}+\ket{0001111}+\ket{1111111}) / 4 \tag{11}
\end{align}

さて、いままで説明してきた変換は、スタビライザー状態をスタビライザー状態に変換するものです。スタビライザー状態というのは、パウリ演算子のテンソル積（パウリ群の要素）によってスタビライズされる状態だったので、別の言い方をすると、パウリ群の要素をパウリ群の要素に変換する共役作用（ユニタリ変換）です。すなわち、任意の$g \in G_n$（$G_n$は$n$量子ビットでのパウリ群）に対して、

U g U^{\dagger} \in G_n  \tag{12}

を満たす演算子$U$の集合に注目し説明してきたわけです。このように定義された演算子のことを「ノーマライザー(normalizer)」または「Clifford演算子」と言い⁵、これらを要素とする集合を$N(G_n)$と書きます。

スタビライザー形式における測定

ユニタリーゲートの作用をスタビライザー形式で記述できたので、次に「測定」について考えてみます。量子回路において測定というと、$Z$基底（$\ket{0},\ket{1}$）で測定をして0または1という値を得る（スピンの言葉で言うと$+1$か$-1$、あるいはupかdown）、ということをまずイメージするかもしれませんが、$X$基底($\ket{+},\ket{-}$)や$Y$基底($\ket{i}$,$\ket{-i}$)⁶での測定もあります。一般には、測定可能な物理量はエルミート演算子に対応づけられてオブザーバブルと呼ばれています。$X$基底、$Y$基底、$Z$基底で測定するというのは、実は各々$X,Y,Z$というオブザーバブルを測定することに他なりません。

量子情報理論の文脈でよく出てくるオブザーバブルは、パウリ演算子またはそのテンソル積です⁷。例えば、演算子$Z_1 \otimes Z_2$を測定するというのはどういうことかというと、1番目の量子ビットに対して$P_0 = (I+Z)/2 = \ket{0}\bra{0}$または$P_1 = (I-Z)/2 = \ket{1}\bra{1}$という射影演算を実行して（どっちが実行されるかは確率的に決定）、2番目の量子ビットに対して同様に$P_0$または$P_1$という射影演算を実行して、$\ket{0}\ket{0}, \space \ket{0}\ket{1}, \space \ket{1}\ket{0}, \space \ket{1}\ket{1}$のどれかの状態を得るという操作です。このとき、パウリ$Z$の固有値（$Z$方向のスピンの値）は$\ket{0}$に対しては$+1$、$\ket{1}$に対しては$-1$なので、$Z_1 \otimes Z_2$の測定値は、$\ket{0}\ket{0}, \space \ket{0}\ket{1}, \space \ket{1}\ket{0}, \space \ket{1}\ket{1}$の各々に対して順に$+1,-1,-1,+1$になります⁸。あるいは、別の例ですが、演算子$X_1 \otimes Y_2$を測定するというのは、1番目の量子ビットに対して$P_{+}=(I+X)/2=\ket{+}\bra{+}$または$P_{-}=(I-X)/2=\ket{-}\bra{-}$という射影演算を実行し、2番目の量子ビットに対して$P_{+i}=(I+Y)/2=\ket{i}\bra{i}$または$P_{-i}=(I-Y)/2=\ket{-i}\bra{-i}$という射影演算を実行し、状態および測定値を得るということです。この場合、測定後の状態としてあり得るのは、$\ket{+}\ket{i}, \space \ket{+}\ket{-i}, \space \ket{-}\ket{+i}, \space \ket{-}\ket{-i}$で、各々に対応した測定値は、$+1,-1,-1,+1$です。この例を延長させればわかるように、パウリ演算子のテンソル積（つまりパウリ群の要素）を測定したときの測定値は$+1$または$-1$です。これはパウリ演算子のテンソル積の固有値が$+1$または$-1$になっていることに対応しています。

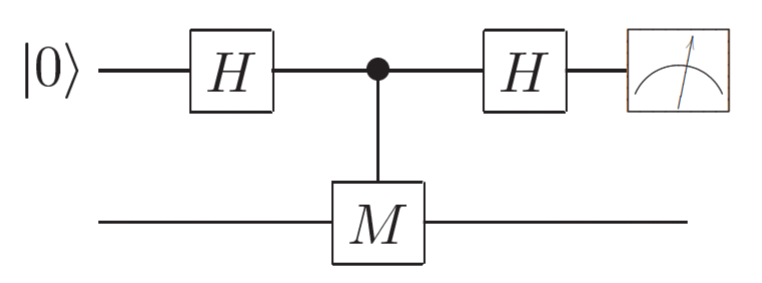
量子回路においてある特定の量子ビットを測定（例えば$Z$基底で測定=オブザーバブル$Z$を測定）すると測定値（に対応した指標、すなわち0か1）を得ることができますが、状態自体は壊れてしまいます。射影された状態も合わせて得たい場合は、以下のようにアンシラを1つ加えて間接測定をします。

これでオブザーバブル$M$を測定したときの測定値（に対応した指標$0$または$1$）を得ると同時に、射影された状態も得ることができます。誤り訂正でよく出てくる基本回路なので、覚えておきましょう。

測定のイメージができたところで、一般論に移ります。スタビライザー群$S=<g_1, \cdots , g_l >$に対応したスタビライザー状態$\ket{\psi} \in V_s$のもとで何らかのオブザーバブル$g \in G_n$を測定することを考えます（冒頭で証明したように有意味な$g$はエルミートなのでオブザーバブル、つまり物理的に測定可能な量とみなせます）。さて、スタビライザー群$S$はどのように変化するでしょうか？以下に示す2つの場合があり得ます。

(1) $g$は$S$の生成元のすべてと可換
(2) $g$は$S$の生成元のどれか1つ以上と反可換

まず(1)の場合です。$g$は$g_j$と可換なので同時対角化が可能であり、同時固有状態をもちます。つまり、$g_j$の固有状態$\ket{\psi}$（固有値$+1$）は、$g$の固有状態でもあります。したがって、$g \ket{\psi} = a \ket{\psi}$と書けます。$g$はユニタリでエルミートなので、固有値$a$は実数値かつ$a^{2}=1$です。すなわち、$g \ket{\psi} = \pm \ket{\psi}$です。したがって、$g$または$-g$は$S$の要素ということになります。$g$が$S$の要素だったとすると、$\ket{\psi}$のもとで$g$を測定した結果は、100%の確率で$+1$です。なぜなら、$\ket{\psi}$は$g$の固有値$+1$に対する固有状態だからです。あるいは、$-g$が$S$の要素だったとすると、$\ket{\psi}$のもとで$g$を測定した結果は、100%の確率で$-1$です。いずれにしても、測定後の状態は$\ket{\psi}$のままです。したがって、この場合、測定の前後で$S$は不変です。つまり、

S = <g_1,g_2, \cdots , g_l > \rightarrow S^{\prime} = <g_1, g_2, \cdots , g_l >  \tag{13}

となります。

次に(2)の場合です。「1つ以上と反可換」と言いましたが、実は反可換なものをいつでも「1つ」にできます。例えば、$g$は$g_1, \space g_2, \space g_3$と反可換で$g_4$以降と可換だったとします。この場合、$g_1$をそのままにして$g_2,\space g_3$に$g_1$をかけたものを新たな$g_{2}^{\prime} = g_1 g_2, \space g_{3}^{\prime} = g_1 g_3$とすると、$g$は$g_{2}^{\prime}, \space g_{3}^{\prime}$と可換になり、かつ、このように置き換えた生成元は依然として$S$の生成元です。これを一般化すれば、どんな場合でも反可換な生成元を1つにすることができます。

ということで、$g$は$g_1$と反可換で残りすべてと可換だったという前提で議論を進めます。(1)の場合と違い、$\ket{\psi}$は$g,-g$の固有状態ではないので$g$を測定して100%の確率で特定の測定値を得るということはありません。状態$\ket{\psi}$のもとでオブザーバブル$g$を測定して測定値が$+1$だったとき、状態は以下のように射影されます。

\ket{\psi} \rightarrow \ket{\psi^{+}} = \frac{I+g}{2} \ket{\psi}  \tag{14}

測定値が$-1$だったとき、状態は以下のように射影されます。

\ket{\psi} \rightarrow \ket{\psi^{-}} = \frac{I-g}{2} \ket{\psi}  \tag{15}

測定値が$+1,-1$になる確率を各々$p(+1),p(-1)$とすると、それらは射影演算子とトレースを使って、

\begin{align}
p(+1) &= Tr(\frac{I+g}{2} \ket{\psi} \bra{\psi})  \\
p(-1) &= Tr(\frac{I-g}{2} \ket{\psi} \bra{\psi})  \tag{16}
\end{align}

と書くことができます⁹。$g_1 \ket{\psi} = \ket{\psi}, \space g_1 g = -g g_1, g^{\dagger}=g$なので$p(+1)$は、

\begin{align}
p(+1) &= Tr(\frac{I+g}{2} \ket{\psi} \bra{\psi})  \\
&= Tr(\frac{I+g}{2} g_1 \ket{\psi} \bra{\psi}) \\
&= Tr(g_1 \frac{I-g}{2} \ket{\psi} \bra{\psi}) \\
&= Tr(\frac{I-g}{2} \ket{\psi} \bra{\psi} g_{1}^{\dagger}) \\
&= Tr(\frac{I-g}{2} \ket{\psi} \bra{\psi}) \\
&= p(-1)  \tag{17}
\end{align}

と変形でき、$p(+)=p(-1)=1/2$が成り立つことがわかります。

測定値が$+1$だった場合、状態は$\ket{\psi^{+}}$になっているので、もはや生成元$g_1$はこのスタビライザー群の要素ではありません。$g \ket{\psi^{+}} = \ket{\psi^{+}}$が成り立つので、$g_1$を$g$に置き換えたものが新たな生成元になります。一方、測定値が$-1$だった場合、状態は$\ket{\psi^{-}}$になっており、$-g \ket{\psi^{-}} = \ket{\psi^{-}}$が成り立つので、$g_1$を$-g$に置き換えたものが新たな生成元になります。つまり、測定値が$+1$だった場合、

S = <g_1,g_2, \cdots , g_l\
> \rightarrow S^{\prime} = <g, g_2, \cdots , g_l>  \tag{18}

で、測定値が$-1$だった場合、

S = <g_1,g_2, \cdots , g_l> \rightarrow S^{\prime} = <-g, g_2, \cdots , g_l>  \tag{19}

という具合に生成元が変化します。

Gottesman-Knillの定理

ユニタリゲートと測定の操作を状態ベクトルの変化ではなく、スタビライザー形式、つまり生成元の変化によって記述することができました。量子ビット数が$n$であれば$n$個の生成元によってユニークなスタビライザー状態を得ることができます。したがって、この$n$個の生成元の変化を追っかければ、それが状態変化を追っかけることに等しくなります。ここで気づいていただきたいのは、スタビライザー形式を使うことで、とても効率的に量子計算をシミュレートできそう、ということです。$n$量子ビットの状態ベクトルの変化をシミュレートしようとするとその状態を記述するのに$2^{n}$個のメモリ（複素数配列）を用意して1つのゲートあたり膨大な行列計算をする必要がありますが、スタビライザー形式を使うと、用意しておくべきメモリは生成元と同じ数$n$個で十分あり、1回のゲート操作は対応した変換規則を適用するだけで良いです。ということで、古典コンピュータでも十分量子計算がシミュレーションできるのでは！？、、とすると、量子コンピュータなんて苦労して開発しても意味がないのでは！？と一瞬思ってしまいます。が、そんなことはありません、というお話をこれからします。

スタビライザー形式におけるユニタリゲートを説明したときに、スタビライザー形式で記述できるのは、パウリ群の要素をパウリ群の要素に変換する演算子（ノーマライザーまたはClifford演算子、以下Clifford演算子という用語で統一します）であるという説明をしました。これはユニタリ演算子全体ではなく、ある性質をもった部分集合に対応した演算です。つまり、すべてのユニタリ演算をClifford演算で置き換えられるわけではありません。とすると、このClifford演算というのは、ユニタリ演算全体からすると、どのように限定された演算子集合なのでしょうか、ということが気になってきます。その答えは以下の定理によって与えられます¹⁰。

＜定理１＞

$U$は$n$量子ビットに働くユニタリ演算子であり、もし$g \in G_n$ならば$U g U^{\dagger} \in G_n$という性質を持つとします。このとき$U$はグローバル位相を除いて$O(n^2)$個のアダマール、位相、および制御NOTゲートで構成できます。

つまり、Clifford演算はアダマール、位相、制御NOTゲートという3つの基本ゲートで構成される、ユニタリ演算子集合の部分集合です。$X,Y,Z$ゲートやそれを制御化したゲートもこの3つの基本ゲートで構成されるので、感覚的には部分集合といってもかなり広い範囲をカバーしているような気もします。制御ゲートも含まれるのでエンタングルも普通に記述できそうです。しかし、$T$ゲートやToffoliゲートはどう頑張っても上記3つの基本ゲートでは構成することができません。パウリ演算子をTゲートで共役をとると、もはやパウリ演算子になりませんし、Toffoliゲートについても同様で共役作用の結果はパウリ演算子のテンソル積にはなりません。やはり上記3つの基本ゲートだけではユニバーサルにはなりません。

では、上記定理を証明してみます。

【証明】

数学的帰納法で証明します。

まず1量子ビットに対するパウリ群の要素、すなわちパウリ演算子をパウリ演算子に変換する$U \in N(G_1)$が有限個のアダマールおよび位相ゲートで構成できることを示します（制御NOTは2量子ビット演算なので除きます）。$X$を$Z$、$Z$を$X$に変換する演算子は$H$です($Z=HXH, X=HZH$)。$X$を$Y$、$Y$を$X$に変換する演算子は$S$および$S^{\dagger}$です($Y=SXS^{\dagger}, X=S^{\dagger} Y S$)。$Y$を$Z$、$Z$を$Y$に変換する演算子は$HS$および$(HS)^{\dagger}$です($Z=-HSY(HS)^{\dagger},Y=-(HS)^{\dagger}ZHS$)。$X,Y,Z$をそれ自身に変換する演算子は恒等演算子$I$ですが、これはアダマールで構成できます($I=HH$)。したがって、1量子ビットに対する$U \in N(G_1)$は有限個のアダマールおよび位相ゲートで構成することができます。

次に、$(n+1)$量子ビットについて考えます。$(n+1)$量子ビットの任意の状態は、

\ket{\Psi} = \ket{0} \otimes \ket{\psi} + \ket{1} \otimes \ket{\phi}  \tag{20}

のように書けます。基底状態の重ね合わせの中で、1番目の量子ビットが$\ket{0}$になっている項と$\ket{1}$になっている項を分けて書いたと思えば良いです。これに対して$U \in N(G_{n+1})$を演算して、

\begin{align}
U \ket{\Psi} &= U(\ket{0} \otimes \ket{\psi}) + U(\ket{1} \otimes \ket{\phi}) \\
&= (\ket{0} \otimes \ket{\psi_1} + \ket{1} \otimes \ket{\psi_2}) + (\ket{0} \otimes \ket{\phi_1} + \ket{1} \otimes \ket{\phi_2}) \tag{21}
\end{align}

となったとします。

1番目の量子ビットに対する$Z$に共役作用$U$を施したものを$M$とおきます。

M = U(Z \otimes I^{\otimes n})U^{\dagger}  \tag{22}

$U$の定義から$M$は$G_{n+1}$の要素です。そうすると、式(21)の前半$U (\ket{0} \otimes \ket{\psi}$は、

\begin{align}
U (\ket{0} \otimes \ket{\psi} &= U \frac{I \otimes I^{\otimes n} + Z \otimes I^{\otimes n}}{2} (\ket{0} \otimes \ket{\psi}) \\
&= \frac{1}{2} U (I \otimes I^{\otimes n} + Z \otimes I^{\otimes n}) U^{\dagger} U (\ket{0} \otimes \ket{\psi}) \\
&= \frac{1}{2} (I+M) U(\ket{0} \otimes \ket{\psi}) \\
&= \frac{1}{2} (I+M) (\ket{0} \otimes \ket{\psi_1} + \ket{1} \otimes \ket{\psi_2}) \\
&= \frac{1}{2} (I+M) (\ket{0} \otimes \ket{\psi_1}) \\
&= \frac{1}{\sqrt{2}} (I+M) (\ket{0} \otimes U^{\prime} \ket{\psi})  \tag{23}
\end{align}

とできます。ここで、$U^{\prime}$は$U^{\prime} \ket{\psi} = \frac{1}{\sqrt{2}} \ket{\psi_1}$を満たすユニタリ演算子として定義しました。

1番目の量子ビットに対する$X$に共役作用$U$を施したものを$N$とおきます。

N = U(X \otimes I^{\otimes n})U^{\dagger}  \tag{24}

$U$の定義から$N$は$G_{n+1}$の要素です。そうすると、式(21)の後半$U (\ket{1} \otimes \ket{\phi}$は、

\begin{align}
U(\ket{1} \otimes \ket{\phi}) &= U (X \otimes I^{\otimes n}) (\ket{0} \otimes \ket{\phi}) \\
&= U (X \otimes I^{\otimes n}) U^{\dagger} U (\ket{0} \otimes \ket{\phi}) \\
&= NU (\ket{0} \otimes \ket{\phi}) \\
&= \frac{1}{\sqrt{2}} N (I+M) (\ket{0} \otimes U^{\prime} \ket{\phi}) \\
&= \frac{1}{\sqrt{2}} (I-M) N (\ket{0} \otimes U^{\prime} \ket{\phi}) \tag{25}
\end{align}

とできます。最後の等号は、$M$と$N$が定義より反可換であることを使いました。

結局、式(20)は、

\begin{align}
U \ket{\Psi} &= \frac{1}{\sqrt{2}} (I+M) (\ket{0} \otimes U^{\prime} \ket{\psi}) + \frac{1}{\sqrt{2}} (I-M) N (\ket{0} \otimes U^{\prime} \ket{\phi}) \tag{26}
\end{align}

と書き直すことができます。

さらに、

\begin{align}
M &= X \otimes M^{\prime} \\
N &= Z \otimes N^{\prime} \tag{27}
\end{align}

となるように$M^{\prime},N^{\prime} \in G_n$をもってきます¹¹。

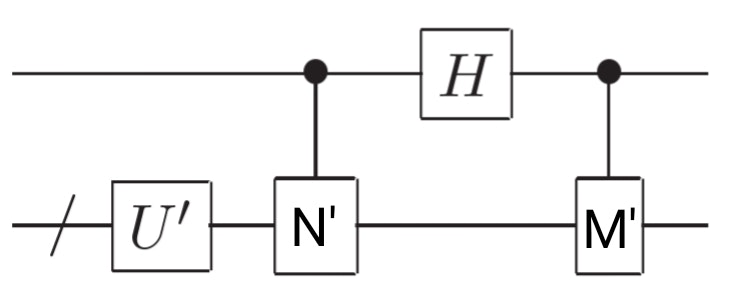
そうすると、いま考えている演算$U$は、以下の量子回路で実現できます。

本当かどうか確認してみます。この量子回路を表す$U$は、

\begin{align}
U &= (\ket{0}\bra{0} \otimes I^{\otimes n} + \ket{1}\bra{1} \otimes M^{\prime}) (H \otimes I^{\otimes n}) (\ket{0}\bra{0} \otimes I^{\otimes n} + \ket{1}\bra{1} \otimes N^{\prime}) (I \otimes U^{\prime}) \\
&= (\ket{0}\bra{0} H \otimes I^{\otimes n} + \ket{1}\bra{1} H \otimes M^{\prime}) (\ket{0}\bra{0} \otimes U^{\prime} + \ket{1}\bra{1} \otimes N^{\prime} U^{\prime}) \\
&= \frac{1}{\sqrt{2}} (\ket{0}\bra{0} \otimes U^{\dagger} + \ket{0}\bra{1} \otimes N^{\prime} U^{\prime} + \ket{1}\bra{0} \otimes M^{\prime} U^{\prime} - \ket{1}\bra{1} \otimes M^{\prime} N^{\prime} U^{\prime}) \tag{28}
\end{align}

です。これを$\ket{\Psi} = \ket{0} \otimes \ket{\psi} + \ket{1} \otimes \ket{\phi}$に演算します。

\begin{align}
U \ket{\Psi} &= \frac{1}{\sqrt{2}} (\ket{0}\bra{0} \otimes U^{\dagger} + \ket{0}\bra{1} \otimes N^{\prime} U^{\prime} + \ket{1}\bra{0} \otimes M^{\prime} U^{\prime} - \ket{1}\bra{1} \otimes M^{\prime} N^{\prime} U^{\prime}) (\ket{0} \otimes \ket{\psi} + \ket{1} \otimes \ket{\phi}) \\
&= \frac{1}{\sqrt{2}} (\ket{0} \otimes U^{\dagger} \ket{\psi} + \ket{1} \otimes M^{\prime} U^{\prime} \ket{\psi} + \ket{0} \otimes N^{\prime} U^{\prime} \ket{\phi} - \ket{1} \otimes M^{\prime} N^{\prime} U^{\prime}) \\
&= \frac{1}{\sqrt{2}} (\ket{0} \otimes U^{\dagger} \ket{\psi} + X \ket{0} \otimes M^{\prime} U^{\prime} \ket{\psi} + \ket{0} \otimes N^{\prime} U^{\prime} \ket{\phi} - X \ket{0} \otimes M^{\prime} N^{\prime} U^{\prime}) \\
&= \frac{1}{\sqrt{2}} (I+M) (\ket{0} \otimes U^{\prime} \ket{\psi}) + \frac{1}{\sqrt{2}} (I-M)N (\ket{0} \otimes U^{\prime} \ket{\phi}) \tag{29}
\end{align}

となり、式(26)と同じ結果になることが確認できました。

ここで、$U^{\prime}$は何らかのユニタリ演算でした。いま$U^{\prime}$はアダマール、位相、制御NOTゲートの組み合わせで構成されているものとします。上で示した量子回路はアダマールゲート$H$および$M^{\prime}$と$N^{\prime}$というパウリ群$G_n$の要素を制御ゲート化したものを加えた構成になっているので、制御$X$（制御NOT）、制御$Y$、制御$Z$をアダマール、位相、制御NOTゲートで置き換えることができれば、この証明の大半ができたことになります。

制御$X$は制御NOTなので自明です。制御$Z$は、

---*---     -----*-----
   |     =       |
---Z---     --H--X--H--

と置き換え可能です。制御$Y$は、$Y=iXZ$なので、

---*---     --*--*--*--     -----*-----*--S--
   |     =    |  |  |    =       |     |
---Y---     --Z--X--i--     --H--X--H--X-----

と置き換え可能です。ここでiと書いたのは、

\begin{pmatrix}
i & 0\\
0 & i
\end{pmatrix}  \tag{30}

という演算を表しています。これがなぜ1番目の量子ビットに$S$（位相ゲート）をかけたもの等しいかは、

\begin{align}
& \ket{0}\bra{0} \otimes I + \ket{1}\bra{1} \otimes e^{ia} I \\
&= (\ket{0}\bra{0} + e^{ia} \ket{1}\bra{1}) \otimes I \\
&= \begin{pmatrix}
1 & 0\\
0 & e^{ia}
\end{pmatrix} \otimes I \tag{31}
\end{align}

において、$a = \pi/2$としてみればわかります。

これで、$N(G_{n})$の要素がアダマール、位相、制御NOTゲートで構成されるなら、$N(G_{n+1})$の要素もアダマール、位相、制御NOTゲートで構成されることがわかりました。したがって、数学的帰納法により、$U \in N(G_{n+1})$は、アダマール、位相、制御NOTゲートで構成されるということになります。

最後に、その個数が$O(n^2)$のオーダーであることについてです。ちょうどいま説明したように、制御$X$は（当たり前ですが）1個の制御NOTで置き換えられます。制御$Z$は2個のアダマールと1個の制御NOT、制御$Y$は2個のアダマール、1個の位相、2個の制御NOTで置き換えられます。ゲート種別を区別しないとするともっとも多いのは制御$Y$の5個です。n量子ビットの各生成元に含まれるパウリ演算子の個数は高々$n$個なので、$M^{\prime},N^{\prime}$には各々最大で$5n$個のアダマール、位相、制御NOTゲートが含まれます。それに1個の単独のアダマールがあるので合計すると$5n+5n+1=10n+1$個となります。$n$量子ビットと$n+1$量子ビットに含まれるアダマール、位相、制御NOTゲートの個数の差分が$n$に比例するということなので、$n+1$量子ビットに含まれるその個数は$O(n^2)$となります。（証明終）

これで1個のClifford演算が多項式時間（ステップ）で実行できることがわかりました。Clifford演算をベースにした量子計算においては1回以上のClifford演算が必要ですし、初期状態の準備や測定というプロセスも必要になります。その全体の計算量を考慮したとしても、多項式時間（ステップ）に収まり、古典コンピュータで効率的にシミュレート可能であるということを主張しているのが、以下に示す「Gottesman-Knillの定理」です。

＜定理２：Gottesman-Knillの定理＞

「(1)計算基底における状態の作成」「(2)アダマールゲート、位相ゲート、制御NOTゲートによる演算（つまりClifford演算）」「(3)パウリ群の要素をオブザーバブルとした測定」「(4)測定結果の条件に応じた古典的制御」によって実行される量子計算は古典コンピュータで効率的にシミュレートできます。

では、証明してみます¹²。

【証明】

(1)計算基底における状態の作成

$n$量子ビットの状態は$n$個の独立な生成元からなるスタビライザー群によってユニークに決まります。つまり、状態の作成は高々$n$に比例したステップ数で実行できます。

(2)アダマールゲート、位相ゲート、制御NOTゲートによる演算

定理１より$n$量子ビットに対するClifford演算$U \in N(G_n)$は、$O(n^2)$個のアダマールゲート、位相ゲート、制御NOTゲートで構成できます。作成した初期状態に対して、この$U$を$n$個の生成元の各々に対して繰り返し実行するということなので、$O(n^3)$ステップで実行できます。

(3)パウリ群の要素をオブザーバブルとした測定

S^{0} = <g_1,g_2, \cdots , g_n>  \tag{32}

というスタビライザー群で$n$量子ビットのClifford演算後の最終状態が規定されているとします。これに対して$Z$基底で測定を行い、測定結果（測定値に対する指標$m_i \in \{ 0,1 \}$）が$(m_1, m_2, \cdots , m_n)$となる確率$p(m_1, m_2, \cdots , m_n)$を求めることを考えます。以下のような手順で計算できます。

[STEP.1] 測定前の状態$S^{0}$における確率を$p^{0}(m_1, m_2, \cdots , m_n)=1$に初期化する。

[STEP.2] 以下のように$n$個の量子ビットを順に測定シミュレーションしていきながら、生成元を$S^{0},S^{1}, \cdots , S^{n}$、確率を$p^{0}, p^{1}, \cdots , p^{n}$という具合に更新します。

$i$番目の測定に関して、

(a)もし、$Z_i$がすべての生成元と可換で、 $(-1)^{m_i} Z_i \in S^{i}$とすると、$m_i$を観測する確率が100%ということなので、生成元はそのまま$S^{i+1}=S^{i}$とし、確率もそのまま$p^{i+1}=p^{i}$とします。

(b)もし、$Z_i$がすべての生成元と可換で、$(-1)^{m_i \oplus 1} Z_i \in S^{i}$とすると、$m_i$を観測する確率が0%ということなので、この時点で求めたい確率は0として結果を返します（以降の測定をしても、どうせ結果は0なので）。

(c)もし、それ以外の場合、つまり$(-1)^{m_i} Z_i$が生成元のうちのどれかと反可換だった場合、先程説明した手続きに従い、反可換な生成元を1つだけにしておきます。その生成元を$(-1)^{m_i} Z_i$に置き換えたものを新たな生成元S^{i+1}とし、$m_i$が観測される確率は$1/2$なので$p^{i+1}=p^{i}/2$とします。

$i=i+1$として繰り返します。$i$が$n$になったら[STEP.3]に移ります。

[STEP.3] STEP.2をn回繰り返した結果得られた、最後の$p^{n}$を求めたい確率$p(m_1, m_2, \cdots , m_n)$とします。

以上の測定手順は、$n$量子ビットの各々の測定において$n$個の生成元との可換・反可換をチェックして、確率を更新していくプロセスなので、必要なステップ数は$O(n^2)$になります。

(4)測定結果の条件に応じた古典的制御

$n$量子ビットの各々の測定結果に応じて古典制御を実行するということなので、$O(n)$のステップ数で実行できます。

以上、(1)(2)(3)(4)の量子計算を総合するとトータルのステップ数は$O(n^3)回$、つまり多項式ステップで実行可能なので、古典コンピュータで効率的にシミュレート可能です。（証明終）

おわりに

スタビライザー形式を使えば、量子状態の変化を状態ベクトルそのものの変化ではなく、生成元という演算子の変化として間接的に、かつ効率的に記述することができることがわかりました。ただし、すべての状態変化ではなく、スタビライザー状態に対するClifford演算の効果に限定されます。限定されるのですべての量子計算をスタビライザー形式（つまりClifford演算）で実行することはできず、Clifford演算は古典コンピュータでもシミュレートできてしまうことになります（Gottesman-Knillの定理）。一方で、この限定が誤り訂正符号を構成する際にうまく働いてくれるのだと思います。今回得た知識をベースに、次回の記事では、誤り訂正が可能となる条件と誤り訂正符号の構成方法について勉強します（予定です）。さらに、その次の記事になると思いますが、具体的な符号をシミュレータで実装し動作確認してみたいと思います。

以上

スタビライザー形式は、トポロジカル符号や測定型の量子計算を理解する上でも、ベースになる大事な話です。 ↩
ニールセン、チャンの「演習10.35」です。 ↩
一般に、$g_1,g_2$が群$G$の要素であるとき、$g_1$に関する$g_2$の共役作用は$g_{1}^{-1} g_{2} g_{1}$で定義されます。 ↩
「シュレーデンガー描像」というのは、状態＝波動関数が時間とともに変化し演算子＝オブザーバブルが変化しないとした量子力学の記述法（描像）で、「ハイゼンベルグ描像」というのは、状態は変化せず演算子の方が時間とともに変化するとした量子力学の記述法（描像）です。量子力学は当初1920年代にシュレディンガーとハイゼンベルグによって異なる形式として定式化されましたが、後にディラックによって両者の同等性が証明されました。量子力学をはじめて学ぶ際にはまずシュレーディンガー方程式が出てくるので、「シュレーデンガー描像」の方が馴染み深いと思います。 ↩
「ノーマライザー(normalizer)」と「Clifford演算子」が正確にどう違ってどう同じなのかよくわかっていません、汗。どちらかというと、「Clifford演算子」という語の方をよく見かけるような気がします。 ↩
$\ket{+}=(\ket{0}+\ket{1})/\sqrt{2}, \space \ket{-}=(\ket{0}-\ket{1})/\sqrt{2}, \space \ket{i}=(\ket{0}+i\ket{1})/\sqrt{2}, \space \ket{-i}=(\ket{0}-i\ket{1})/\sqrt{2}$という定義です（念の為）。 ↩
単なる$X,Y,Z$基底での測定やそれを複数量子ビットにわたって実行した場合に加えて、VQEなどNISQ系の処理では、パウリ演算子のテンソル積として表されたハミルトニアンの期待値を計算するために、その測定が行われたりします。 ↩
量子計算のシミュレータで測定をやって出てくるアウトプットは測定値（$+1$または$-1$）ではなくて、状態$\ket{0},\ket{1}$を区別する指標$0$または$1$なので、この辺りの説明は混乱しがちかもしれません。なので、ちょっと丁寧に説明しています。 ↩
測定操作に対応した射影演算子を$P$、密度演算子を$\rho$とすると、その確率は$Tr(P \rho)$で与えられます。 ↩
ニールセン、チャンの「定理10.6」です。その証明は「演習10.40」の(1)(2)(3)を順に解いていけば完成します。「簡単」と書いてあるのですが結構な難問でした。参考文献2のAPPENDIXを参考にして組み立ててみた証明を以下で示します。 ↩
$M$および$N$が$X \otimes I^{\otimes n}$および$Z \otimes I^{\otimes n}$と反可換だった場合このようにできるのはわかりますが、そうできない$U$もあり得ます、つまり$M$および$N$を$U$を使って定義した結果、$X \otimes I^{\otimes n}$および$Z \otimes I^{\otimes n}$と可換になってしまう場合です。この場合、どこか1つの量子ビットに1量子ビットゲート（例えばアダマール）を演算したものを新たな$U$にすればいつでも反可換にできるので、式(27)のように$M,N$をおくことができます。このような手続きで$U$を変更する場合があったとしても、命題の証明にとっては何の影響ありません、と思います。 ↩
ニールセン、チャンの「定理10.7」です。ニールセン、チャンの非常に簡単な記述の行間を自分なりに補間して、かつ、測定については参考文献3を参考に、証明を組み立ててみました。「効率的にシミュレートできる」という意味を本当はきちんと定義した方が良いのかもしれませんが、ここではとてもラフに指数時間（ステップ）ではなく多項式時間（ステップ）で計算が実行できること、と捉えておきます。また、量子計算理論におけるオーダー記法とか計算のステップをどう定義するべきなのかについて、自分自身あまり慣れていないので、正しくそのオーダーを評価しているのか、、もしかすると怪しいことをやっているかもしれません。が、高々、多項式ステップで計算量が収まるという証明としては、何とかなっているのではと思っています（が、おかしなところがあったらご容赦を。またはご指摘いただけるとありがたいです）。 ↩