この記事は DATUM STUDIO Advent Calendar 2016 17日目の記事です。
わたしとさとよーへー
DATUM STUDIO株式会社 の里洋平と最初に出会った場所は前職の株式会社ドリコムであった。大学院の修士課程で人工知能、情報検索、自然言語処理などを学んだ後、新卒のデータ分析者としてドリコムに入社した私は彼と同じ部署で働き始めることとなった。分析業務のために R 言語に触れ、彼主催の Tokyo.R にも発表者として何度か参加する機会を得た。
ある回の Tokyo.R 終了後の懇親会もついに3次会に突入することとなり、酔っぱらいながら3次会の会場に設定された練馬方面にタクシー向っていた。そのタクシーの中で将来どういうことをしたいのか?という話になり、彼から「いつかはわからないけど近いうちに独立・起業してもっとでっかいことをやろうと思ってるんですよ」という話を聞いた記憶がある(残念ながら私もかなり酔っていたため、いい話だったような気がするのに具体的な日付や詳細を覚えていないのが惜しい)。
分析者としてやっていくために、ひたすら分析スキルを磨かないといけないなと思っていたこの頃(社会人1年目)の自分にとって、独立とか起業とかリスキーな方向へ向かう発想は全くなかったため、このタクシーの中の会話は自分も将来的にはリスクを取って、そういう将来を目指すのもありかもしれないなと思うきっかけの一つとなったのは間違いない。
その年の秋、彼とドリコムにいた酒巻さん(現 DATUM STUDIO 代表取締役)の2名が新しく会社を作って独立する流れとなり、スキルのある人と一緒に働けなくなるのは残念だなと思いつつ、たくましく新天地に向かっていく彼らの姿はなかなか格好良かった。
前職では順調に集まっていたデータ分析チームのコンディションが悪化してしまった時期があり、自分の将来をあれこれ考え、より良い方向に向かってい行くためにちょっとした博打を私もやる必要があった。色々選択肢はあったが、出来たばかりの DATUM STUDIO に3人目のメンバーとして加わることを選択し、彼がタクシーの中で語っていた未来に向かって私も走っていくこととなった。
そんなこんなで激動の約2年を駆け抜け、今に至る。
なぜか Qiita では Ruby + Rails 関連の記事伸びてるので勉強会で初対面の方に「Web エンジニアですか?」と聞かれたこともありましたが、今のところ Python と R をメインに使う分析者です。
ある日の DATUM STUDIO の夜
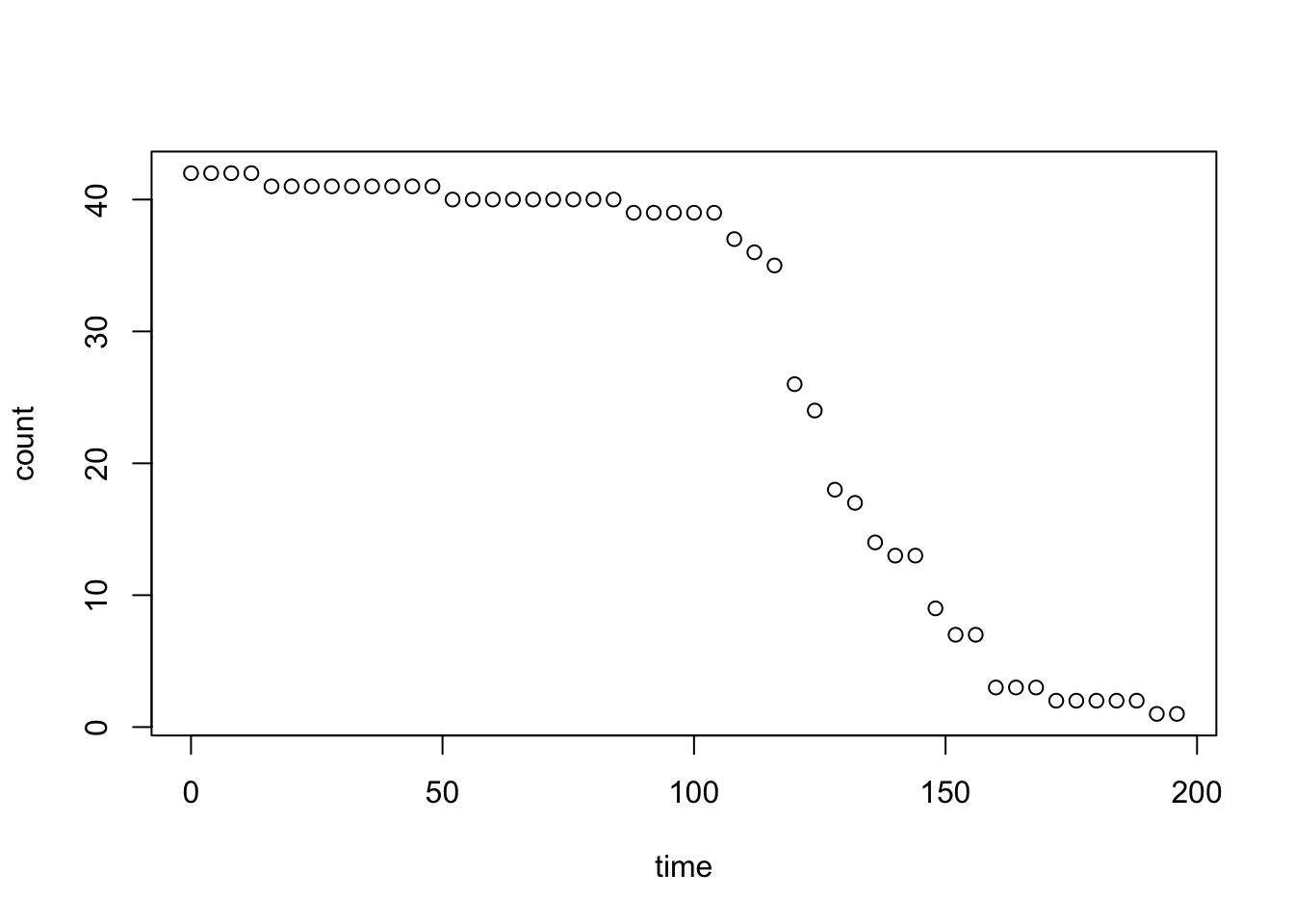
DATUM STUDIO では金曜日の業務後に定期的に社内で飲み会を行っている。ある日の飲み会開始からの時間と部屋に滞在している社員数の関係をプロットしてみると次のようになった。
df <- read.csv("member_count.csv")
plot(count ~ time, data = df)
count: オフィスの滞在人数 [人]
time: 飲み会開始からの経過時間 [分]
この日はそのまま1次会で解散となった。しかし今回の飲み会では飲み足りない人が居たようだ。彼は次のように言った。「次回は2次会まで企画したい。1次会がいい感じに盛り上がった後、多くの仲間を次の会場に案内したい」と。さてどのタイミングで2次会への誘導の声を掛けるのが良いだろうか?
問題に落としてみる
さて、先程の関係を式にすると次のようになる。
y = f(t)
y: オフィスの滞在人数 [人]
t: 飲み会開始からの経過時間 [分]
多くのメンバーに声をかけるには t が増加していったとき y が急激に減少する前に声をかけなければならない。逆に声をかける時間が早すぎると1次会を楽しみきれない。この急激に人数が減少するときの t を特定するという問題になる。
この t を予測するには、先程の y と t の関係式を回帰分析により求め、その後接線の傾きの減少が最大になる点を求めるという問題として考えればよい。これは関数 f を2階微分した値が最小値をとるところと等しいはずである。
ロジスティック曲線を利用した回帰
今回は glm 関数を使用してロジスティック曲線のあてはめ(回帰)を行った後、ロジスティック曲線の式を R の関数を利用して微分、その後2階微分した際に y が最小となる点を optimize 関数を利用して算出してみる。
まずはデータを t、y それぞれ最大値で割り 0 〜 1 の値となるように正規化する。ここでは Hadley 神が作り給うた dplyr パッケージ 利用して加工している。
library(dplyr)
normalized_df <- df %>%
mutate(normalized_time = time / max(time)) %>%
mutate(normalized_count = count / max(count))
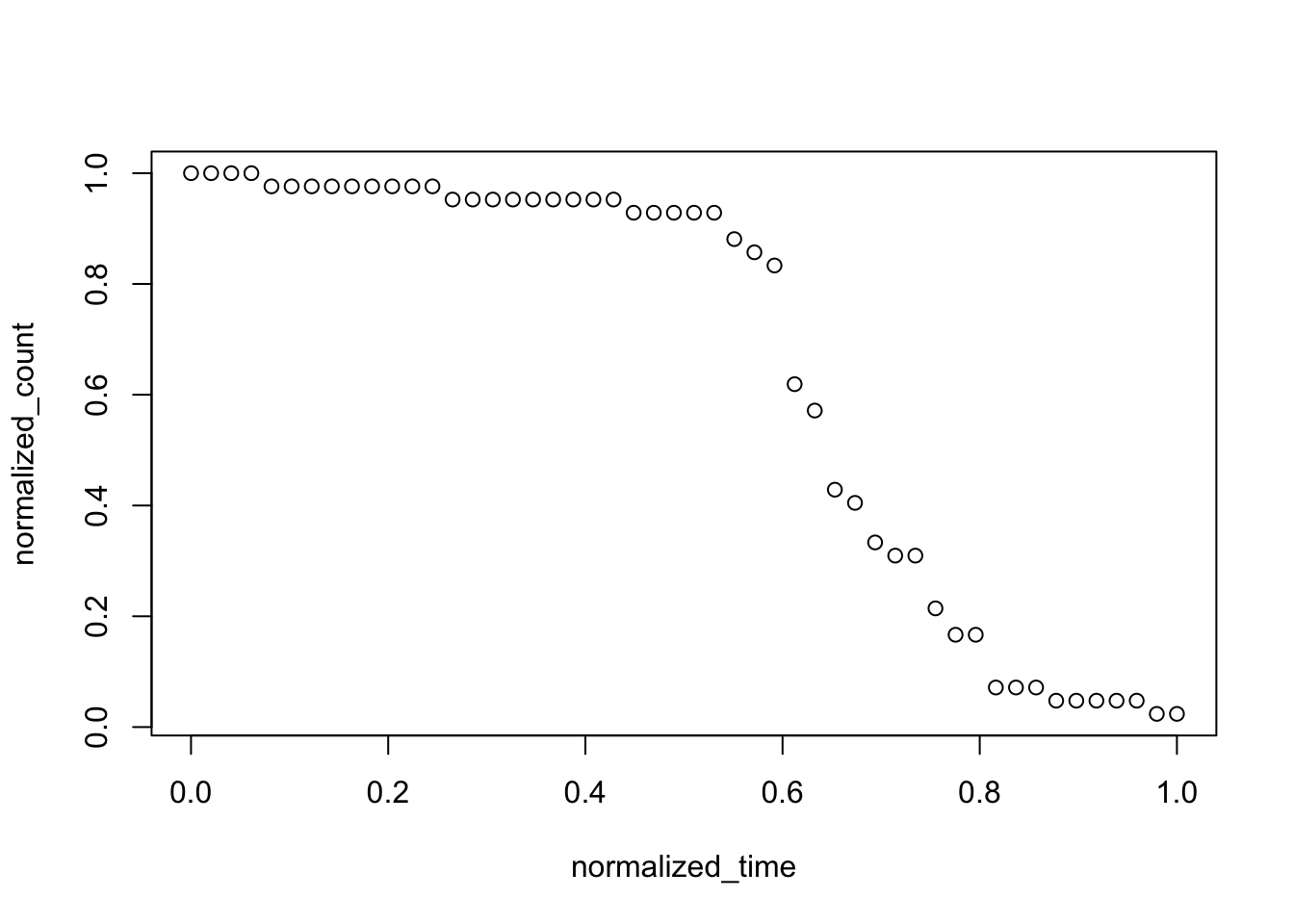
plot(normalized_count ~ normalized_time, data = normalized_df)
この処理により、ロジスティック曲線でフィッティングが可能になった。次は回帰を行う。glm 関数の第一引数に目的変数と説明変数を formula 形式(normalized_count ~ normalized_time)で記述し、data には先程加工したデータフレームを指定する。family に binomial(link="logit") と指定することでロジスティック曲線によるフィッティングが行える。
# ロジスティック曲線による回帰
logistic_curve_model <- glm(
normalized_count ~ normalized_time,
data = normalized_df,
family = binomial(link="logit")
)
作成したモデルを summary 関数で確認してみる。
summary(logistic_curve_model)
##
## Call:
## glm(formula = normalized_count ~ normalized_time, family = binomial(link = "logit"),
## data = normalized_df)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.29077 -0.15130 -0.05772 0.04388 0.36114
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 7.347 2.143 3.428 0.000607 ***
## normalized_time -11.189 3.219 -3.476 0.000510 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 38.2219 on 49 degrees of freedom
## Residual deviance: 1.3743 on 48 degrees of freedom
## AIC: 18.321
##
## Number of Fisher Scoring iterations: 7
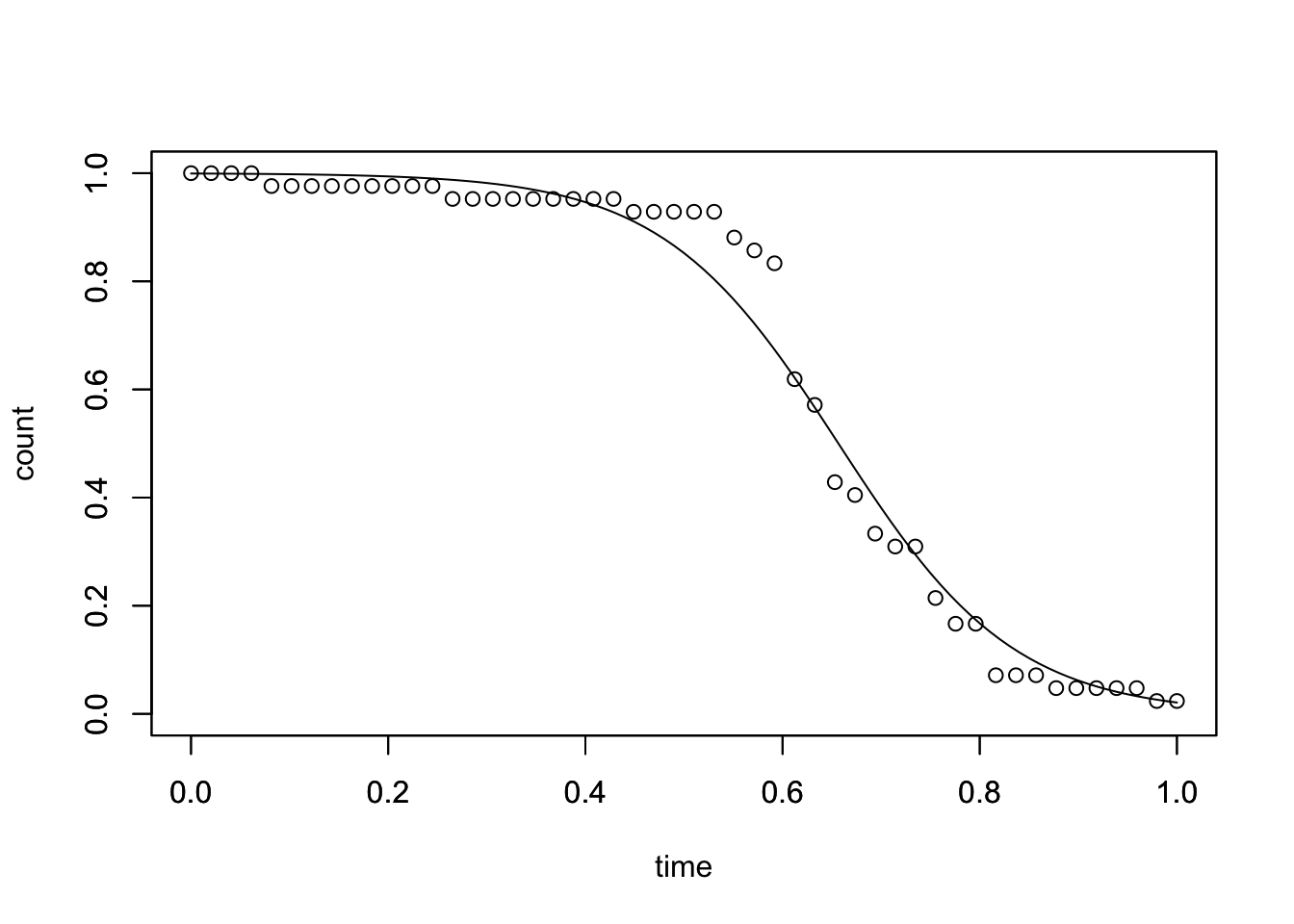
P 値を見る限り良い感じに見える。実際にフィッティング結果をプロットしてみよう。ロジスティック曲線は次の式で表せる。
\begin{align}
y &= f(t)\\
&= \frac{e^{a + bt}}{1 + e^{a + bt}}
\end{align}
定数 a, b は 作成したモデルの coefficients [1], [2] に格納されている。
a <- logistic_curve_model$coefficients[1]
b <- logistic_curve_model$coefficients[2]
f <- function(t) { exp( a + b * t) / (1 + exp( a + b * t)) }
plot(
x = seq(0, 1, 0.01),
y = f(seq(0, 1, 0.01)),
type = "l",
xlim = c(0, 1),
ylim = c(0, 1),
xlab = "time",
ylab = "count"
)
par(new = T)
plot(
normalized_count ~ normalized_time,
data = normalized_df,
xlim = c(0, 1),
ylim = c(0, 1),
xlab = "",
ylab = ""
)
いい感じである。次は変曲点を求めるために下記の式を微分していく。
y = \frac{e^{a + bt}}{1 + e^{a + bt}}
手計算は面倒なので、R を活用し解いてみる。expression 関数で微分する式を定義し、D 関数の第一引数に定義した式、第二引数に対象の変数を指定することで微分できる。
# 変曲点を求める
f_0 <- expression(1 / (1 + exp(-a + -b * t)))
# 1階微分
D(f_0, "t")
これにより以下のように1階微分後の式が得られる。
## exp(-a + -b * t) * b/(1 + exp(-a + -b * t))^2
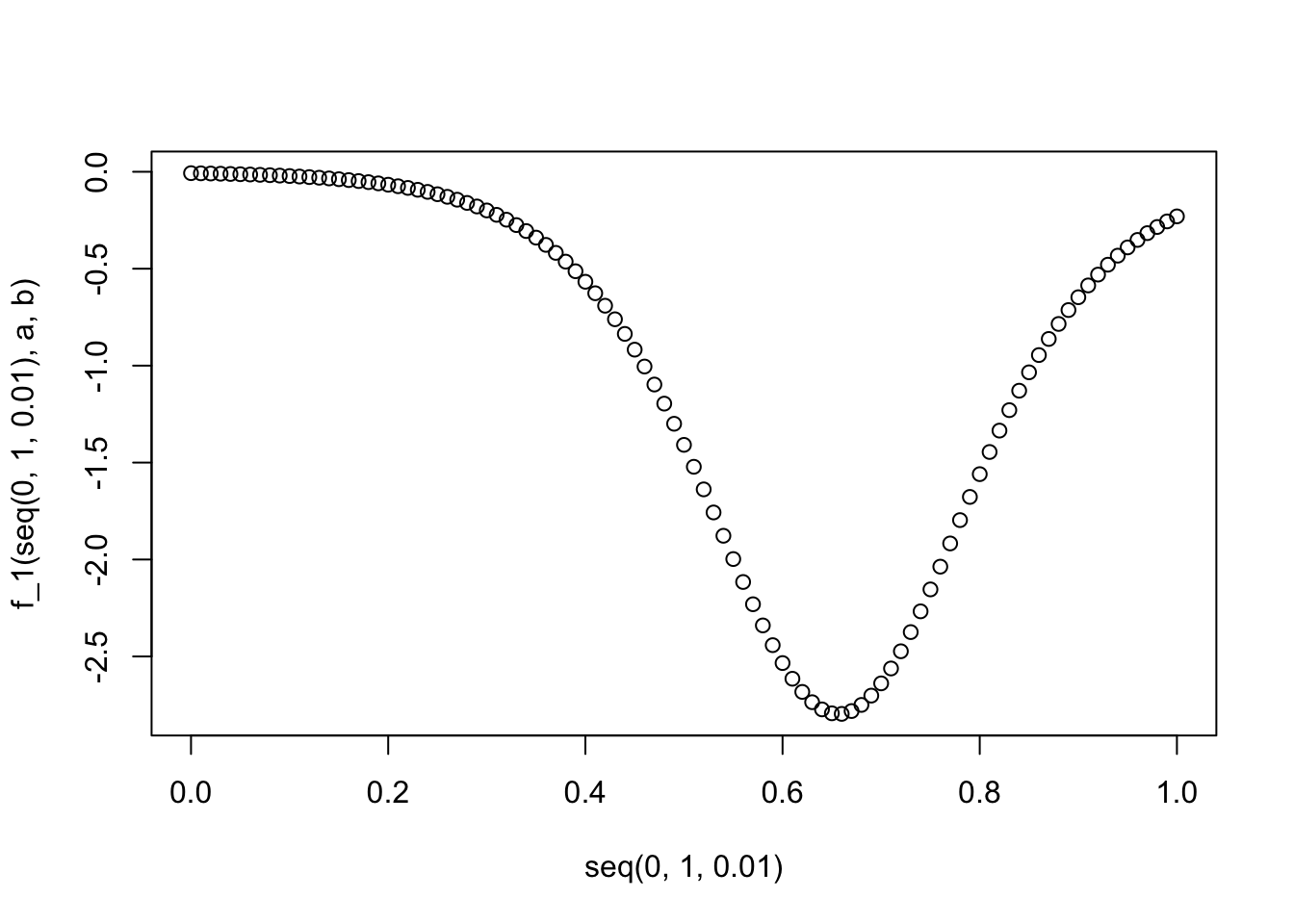
さてこの結果をプロットしてみよう。
f_1 <- function(t, a, b) {
exp(-a + -b * t) * a/(1 + exp(-a + -b * t))^2
}
plot(x = seq(0, 1, 0.01), y = f_1(seq(0, 1, 0.01), a, b))
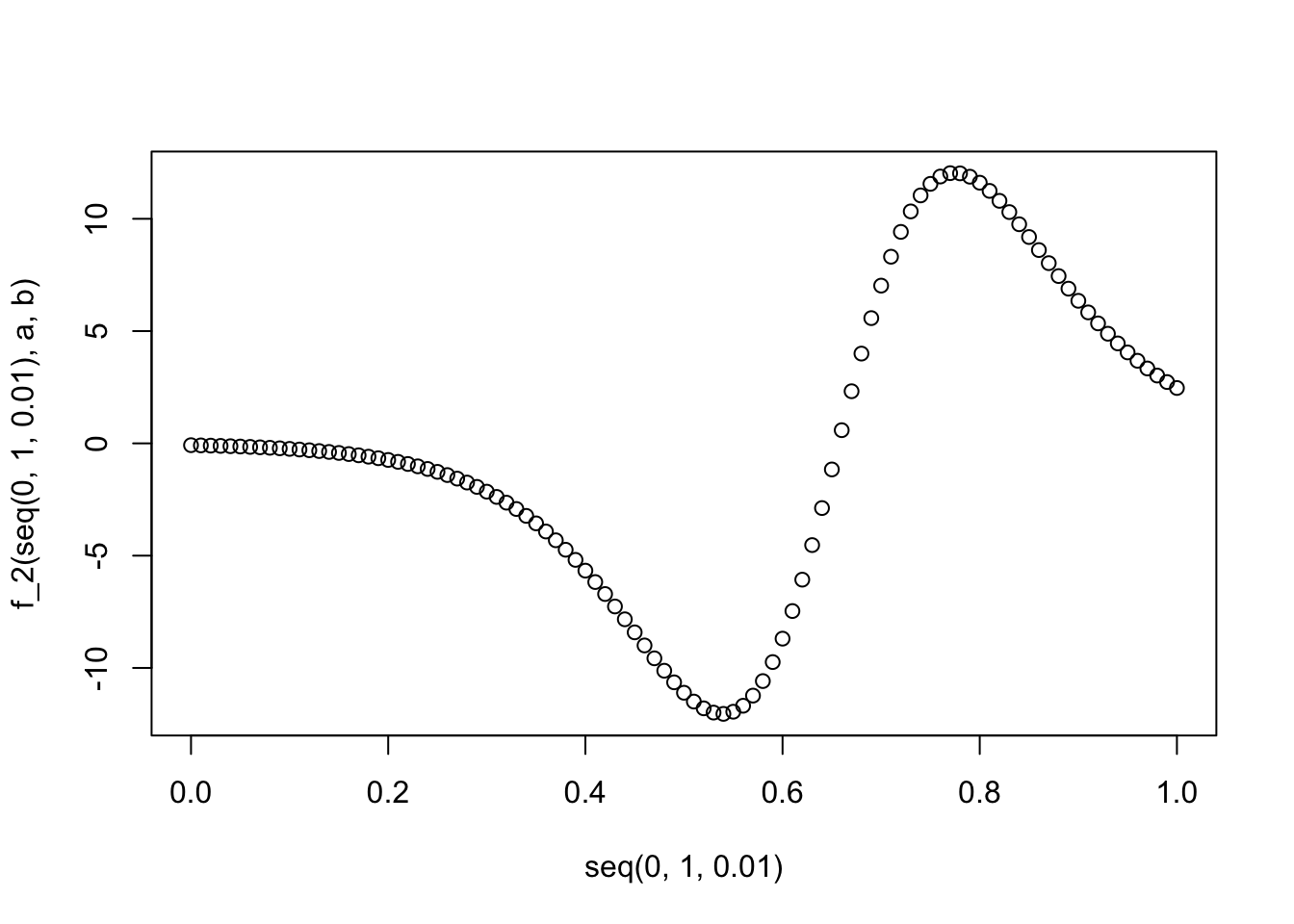
さてそのまま2階微分した結果も求めてみよう。
# 2階微分
D(D(f_0, "t"), "t")
f_2 <- function(t, a, b) {
-(exp(-a + -b * t) * b * b/(1 + exp(-a + -b * t))^2 - exp(-a +
-b * t) * b * (2 * (exp(-a + -b * t) * b * (1 + exp(-a +
-b * t))))/((1 + exp(-a + -b * t))^2)^2)
}
plot(x = seq(0, 1, 0.01), y = f_2(seq(0, 1, 0.01), a, b))
ここまでで回帰式を2階微分したものが得られたので、次は y が最小となる t を optimize 関数を利用し求める。第一引数に対象の変数を引数にとる関数(f_2)を指定し、定数 a, b も引数として指定する。値の上限、加減(今回は t の範囲)を lower、upper 引数に指定する。今回は最小値を求めるので maximum 引数は FALSE を 指定する (TRUE を指定すれば最大値を
とる点を求めることも可能である)。最小となる t を求めた後、正規化前の t の最大値を掛けて、元のスケールに戻す。
# y が最小となる場合の t を求める
opt <- optimize(
f = f_2,
a = a,
b = b,
lower = 0.0,
upper = 1.0,
maximum = FALSE
)
opt_time <- opt$minimum * max(normalized_df$time)
opt_time
## [1] 105.6348
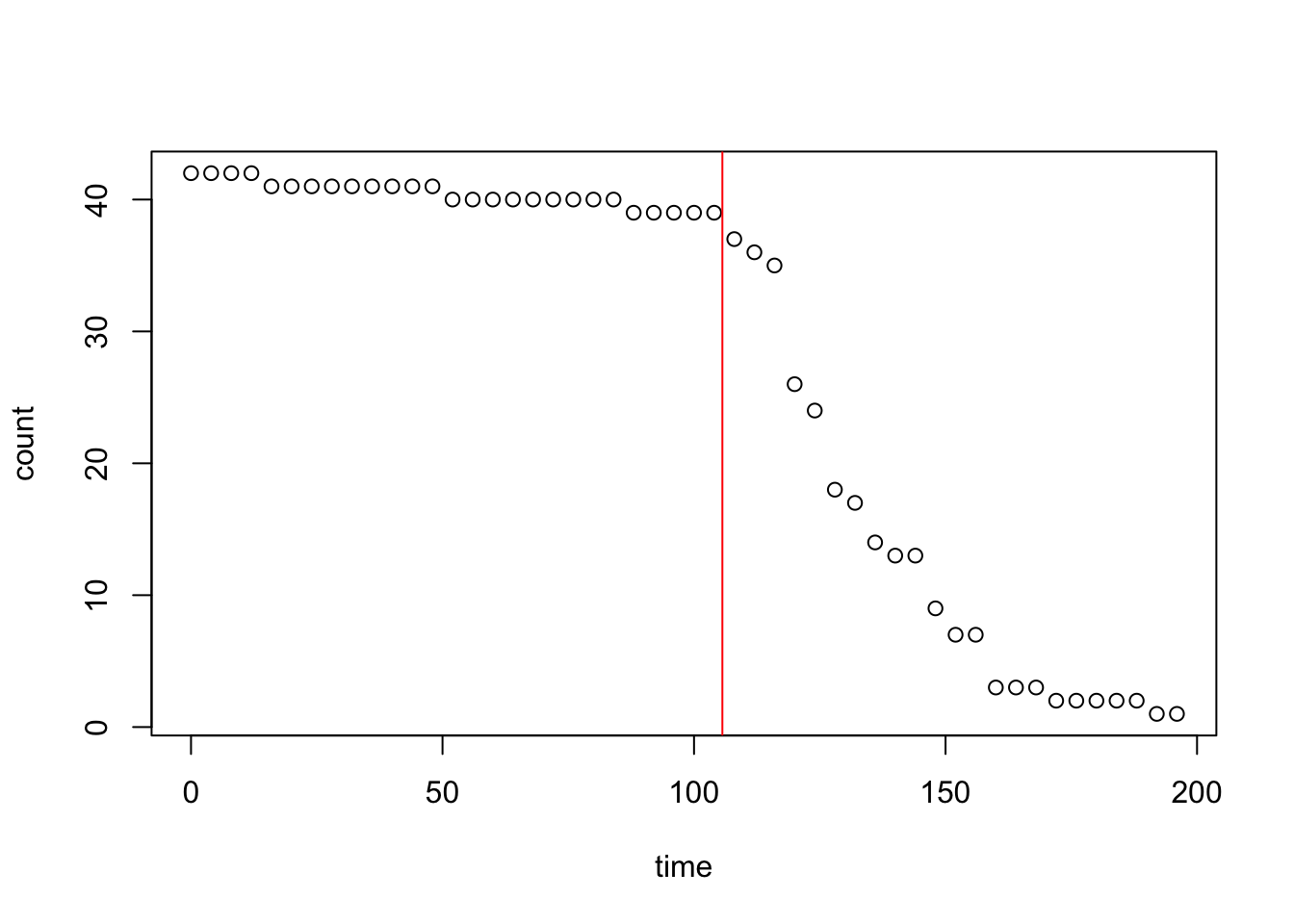
さてこれでこの飲み会における二次会移行に最適な t が求まった。実際に元のグラフにプロットして確認してみよう。赤線が今回求めた t である。
plot(count ~ time, data = df)
par(new = T)
abline(v = opt_time, col = "red")
良い感じに2次会移行に最適な点 t が求まった。
おわりに & これから
あくまで上記の t はこの1回分データのみから算出した結果となる。また使用した説明変数も経過時間のみなのでこのモデルはちょっと貧弱である。この1回の結果をそのまま一般化するのは危険である。実際に運用まで持っていくには、更にデータを多く集め何度も検証しよりよい変数を選択・追加しながらモデルを改善していく必要がある。
つまるところお酒を楽しく何度も飲めばおkということである(ただし飲み過ぎは駄目ですよ)。
※ 注意: 今回使用したデータはこの記事のために作成したデータであり、実際の DATUM STUDIO 社における定例飲み会のデータとは異なる。