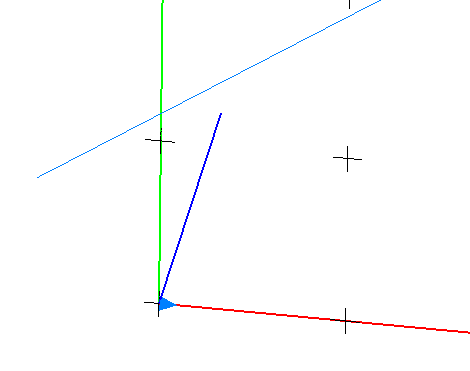
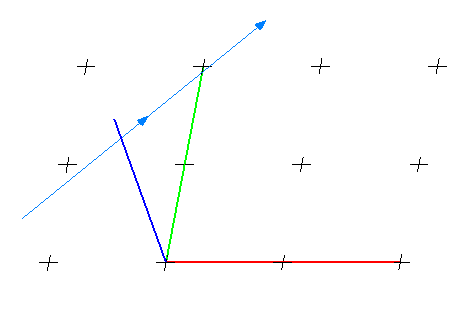
OpenGLで行列を用いてオブジェクトを任意の位置と方向に配置する
OpenGLで直線を描くにはglVertex3d()などを使えば良いが、直線に矢印を付けるのは難儀である。そこで円錐を作成して、直線の両端や中央にセットすれば、一応矢印に見える。
円錐を作成する関数はgluCylinder()であるが、この関数では円錐は原点(0,0,0)にz軸方向にしか作成できない。よって、目的の位置に目的の向きに円錐を移動させる必要がある。そのためのC++のコードを紹介する。
3次元上の配置されているオブジェクトに対して、変換を施す行列は以下の様になる。
\begin{pmatrix}
r00 & r01 & r02 & tx\\
r10 & r11 & r12 & ty\\
r20 & r21 & r22 & tz\\
0 & 0 & 0 & 1
\end{pmatrix}
r00からr22までは、オブジェクトの座標(X,Y,Z)に作用する成分である。
tx,ty,tzは平行移動成分である。
ベクトル(X,Y,Z,1)に先の行列を作用させて(X',Y',Z',1)に変換される時の式は以下の様になる。
\begin{pmatrix}
X'\\
Y'\\
Z'\\
1
\end{pmatrix}
=
\begin{pmatrix}
r00 & r01 & r02 & tx\\
r10 & r11 & r12 & ty\\
r20 & r21 & r22 & tz\\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
X\\
Y\\
Z\\
1
\end{pmatrix}
まず、直線が始点(x1,y1,z1)から終点(x2,y2,z2)までひかれている時、
円錐を終点(x2,y2,z2)まで移動させる行列は以下の様になる。
\begin{pmatrix}
1 & 0 & 0 & x2\\
0 & 1 & 0 & y2\\
0 & 0 & 1 & z2\\
0 & 0 & 0 & 1
\end{pmatrix}
直線の始点や中央に移動させる場合も同様に行列を作成できる。
平行移動は以上になるが、円錐の向きが直線の向きと一致させる必要がある。
円錐の大きさなどはgluCylinder()で指定できるのと、位置は先の平行移動の行列で実行できるので、残るのは向きの設定である。
向きは行列のr00からr22までを回転行列として成分の値をセットする。
まず、直線の単位方向ベクトル(ex,ey,ez)を求める。
C/C++コードの場合、以下の様なコードになるかと思う。
double dx = x2 - x1;
double dy = y2 - y1;
double dz = z2 - z1;
double r = sqrt(dx*dx+dy*dy+dz*dz);
double ex = dx/r;
double ey = dy/r;
double ez = dz/r;
よって、Z軸の向きに作成されいる円錐の向きを(ex,ey,ez)の方向に向かせる、回転行列を作成すれば良いと言う事になる。
回転行列では、最初に円錐をX軸の向きに倒すものを考える。
X軸の向きに倒すには、Y軸周りの1/2π(90°)回転となる。
なお、回転行列についてはWikipediaの「回転行列」を参照。
Ry(\frac{1}{2}π)=
\begin{pmatrix}
0 & 0 & 1\\
0 & 1 & 0\\
-1 & 0 & 0
\end{pmatrix}
円錐をX軸に沿う様にしたので、次はX-Y平面で回転を行う。
X-Y平面での回転は、Z軸周りの回転となる。
Z軸周りの回転行列は以下になる。
Rz(Θ)=
\begin{pmatrix}
\cos Θ & \sin Θ& 0\\
\sin Θ & \cos Θ& 0\\
0 & 0 & 1
\end{pmatrix}
この回転行列を使うには、角度Θを求めて代入するのでは無く、
sinΘとcosΘを求めて、行列の成分を設定する。
直線の単位方向ベクトル(ex,ey,ez)のx,y成分の大きさは、
l=\sqrt{ex^2+ey^2}
lはx-y平面での直角三角形の辺の長さを表すので、
lx=\cos Θ=\frac{ex}{l}\\
ly=\sin Θ=\frac{ey}{l}\\
lz=ez
となるので、行列Rzは以下の様になる。
Rz(Θ)=
\begin{pmatrix}
lx & -ly & 0\\
ly & lx& 0\\
0 & 0 & 1
\end{pmatrix}
次は線とX-y平面との角度φとして、
Y軸周りに角度1/2πだけ回転して、
角度φだけ戻す行列を得る。
Ry(\frac{1}{2π}-φ)=
\begin{pmatrix}
\sin φ & 0 & cos φ\\
0 & 1 & 0\\
-cos φ & 0 & sin φ
\end{pmatrix}\\
となり、sinとcosについては、
cos φ=l\\
sin φ=ez
から
Ry(\frac{1}{2π}-φ)=
\begin{pmatrix}
ez & 0 & l\\
0 & 1 & 0\\
-l & 0 & ez
\end{pmatrix}\\
となり、先の3つの行列を掛け算して、線の方向ベクトルと同じ向きに
なる回転行列は、
Ry(\frac{1}{2π})・Rz(Θ)・Ry(\frac{1}{2π}-φ)=
\begin{pmatrix}
lx・lz & -ly & lx・l\\
ly & lx & ly・l\\
-l & 0 & lz
\end{pmatrix}\\
結局OpenGLに作用させる4x4の行列は、
線分の終点(x2,y2,z2)を用いて
\begin{pmatrix}
X'\\
Y'\\
Z'\\
1
\end{pmatrix}
=
\begin{pmatrix}
lx・lz & -ly & lx・l & x2\\
ly & lx & ly・l& y2\\
-l & 0 & lz & z2 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
X\\
Y\\
Z\\
1
\end{pmatrix}
//描画開始
glPushMatrix();
{
//色
glColor3f(ffR,ffG,ffB);
//円錐の向きの大きさを1にする(単位ベクトル)
GetUnitVector(dx,dy,dz,&ex,&ey,&ez);
//通常行列作成(X-Y平面上の円錐の向き)
double l = sqrt(ex*ex + ey*ey);
GLdouble m1[16] = {
ex*ez, -ey, ex*l, rx,
ey , ex, ey*l, ry,
-l , 0, ez, rz,
0 , 0, 0, 1
};
//OpenGL行列に変換
ConvertToOpenGLMatrix(m1);
//行列の掛け算
glMultMatrixd(m1);
//オブジェクト生成
GLUquadricObj *sphere = gluNewQuadric();
//描画スタイルの設定
gluQuadricDrawStyle(sphere, GLU_FILL);
//円錐の描画
gluCylinder(sphere,baseradius,topradius,height,slice,stacks);
//メモリ解放
gluDeleteQuadric(sphere);
}
glPopMatrix();
なお、一般の行列とOpenGLの行列では、
成分の配置が違うので、一般の行列からOpenGLの行列の変換関数を以下に示す。
void ConvertToOpenGLMatrix(GLdouble m0[16])
{
//変換前
// a0 a1 a2 a3
// a4 a5 a6 a7
// a8 a9 a10 a11
// a12 a13 a14 a15
//変換後
// a0 a4 a8 a12
// a1 a5 a9 a13
// a2 a6 a10 a14
// a3 a7 a11 a15
GLdouble m1[16] = {0};
m1[ 0] = m0[ 0];
m1[ 1] = m0[ 4];
m1[ 2] = m0[ 8];
m1[ 3] = m0[12];
m1[ 4] = m0[ 1];
m1[ 5] = m0[ 5];
m1[ 6] = m0[ 9];
m1[ 7] = m0[13];
m1[ 8] = m0[ 2];
m1[ 9] = m0[ 6];
m1[10] = m0[10];
m1[11] = m0[14];
m1[12] = m0[ 3];
m1[13] = m0[ 7];
m1[14] = m0[11];
m1[15] = m0[15];
memcpy(m0,m1,sizeof(GLdouble)*16);
}
最後に
OpenGLなどの描画系では、行列やベクトルなどを多用する必要があるような気がするので、その辺の勉強が必要と思いました。