近似曲線入門 - 最小二乗法と回帰分析をやさしく理解する

Last updated at 2025-07-16Posted at 2025-07-16

はじめに

「近似曲線」「最小二乗法」「回帰分析」...統計学やデータサイエンスでよく聞く言葉ですが、実際のところ何をしているか理解できていますか？

今回は、数学が苦手な方でも理解できるよう、身近な例を使って分かりやすくまとめてみました。難しい数式は最小限に抑え、「なぜそうなるのか」の理解を重視しています。

記事内には、同じことばの定義が何度か登場したり、似たようなデータの説明を繰り返したりしています。その状況で理解できるようにしたためです。

近似曲線とは「データの中にある物語を見つけること」

身近な例 → カフェの売上分析

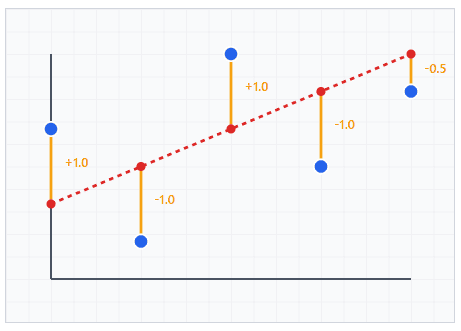
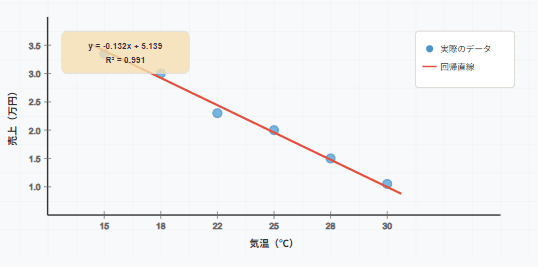
あなたがカフェを経営しているとします。毎日の気温と売上をグラフにしたところ、こんな感じになりました。

点をプロットすると、バラバラに見えますが、よく見ると「気温が高くなるほど売上が下がる」という傾向が見えてきます。これが データの中にある物語 です。

近似曲線は、この物語を「線」で表現したものなのです。

最小二乗法 - 「一番いい線」を見つける方法

なぜ「二乗」なのか？

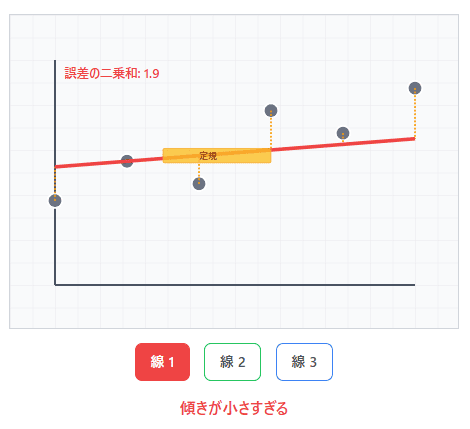
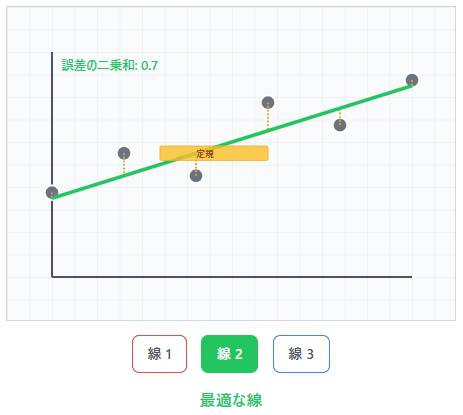
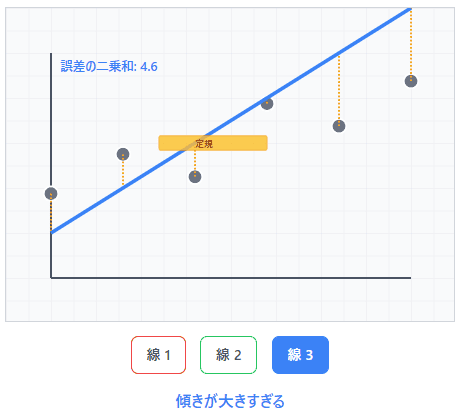
データの点と引いた線との距離を「誤差」と呼びます。最小二乗法は、この誤差を最小にする線を見つける方法です。

なぜ「二乗」するのでしょうか？

プラスとマイナスが相殺されないため
- 単純に足し算すると、+2と-2が相殺されてしまいます
- 二乗すると、+4と+4になり、誤差の大きさが正しく評価できます
大きな誤差をより重視するため
- 誤差2は二乗すると4
- 誤差4は二乗すると16
- 大きな誤差の方が、より強くペナルティを受けます

直感的な理解

想像してみてください。あなたが定規を持って、散らばった点の上に線を引こうとしています。どの角度で引けば、すべての点から「平均的に一番近い」線になるでしょうか？

最小二乗法は、この「一番近い」を数学的に定義し、自動的に見つけてくれる方法なのです。

回帰分析 - 関係性を数値で表現する

回帰分析とは

回帰分析は、「X が Y に与える影響を定量的に測る」手法です。

先ほどのカフェの例で言うと・・

X（説明変数）: 気温
Y（目的変数）: 売上
関係: 気温が1℃上がると、売上が約0.1万円下がる

回帰分析で分かること

傾き（回帰係数）: 関係の強さ
「気温が1℃上がると売上が0.1万円下がる」

切片: 基準値
「気温が0℃のとき、売上は4万円」

決定係数（R²）: 説明力
「気温の変化で売上変動の85%を説明できる」

実際の解釈例

python

# 実際に計算した回帰分析の結果
係数: -0.132  # 気温が1℃上がると売上が0.132万円下がる
切片: 5.139   # 気温0℃のとき売上5.139万円（※外挿のため参考値）
R²: 0.991     # 99.1%の変動を説明可能

この結果から言えること

「猛暑日は売上が落ちる」という仮説が数値で証明された
気温予報を見れば、高い精度で売上を予測できる
ただし、解釈可能範囲は測定データの範囲（15-30℃）に限定される
気温0℃での売上は外挿値のため、実際の予測には使用しない

注意: サンプル数が6点と少ないため、R²が過大評価されている可能性があります。現場では最低 30〜50 点を推奨。

【種類別】どの線を選ぶか

1. 直線（線形回帰）

こんなときに使う！

関係が単純で分かりやすい
「○○が増えると△△も増える」という関係

例: 広告費と売上、勉強時間と成績

2. 非線形回帰

変数間の関係が直線では表現できない場合に使用します。

対数・指数回帰

こんなときに使う！

急激な成長や減衰を示すデータ
「最初は急激、後で緩やか」な関係

例: 人口増加、学習効果、放射性崩壊

多項式回帰

こんなときに使う！

上に凸、下に凸の関係がある
「最適な値がある」という関係
注意：次数を上げるほど柔軟だが過学習リスクが増加

例: 価格と売上（高すぎても安すぎても売れない）

【実践】Pythonで簡単実装

基本的な線形回帰

線形回帰を実装する前に、まずデータの準備から始めましょう。今回はカフェの例で使用した気温と売上のデータを使います。

python

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# データの準備
# 説明変数（X）: 気温データ - reshape(-1, 1)で縦ベクトルに変換
# scikit-learnは2次元配列を期待するため、1次元データを2次元に変換が必要
temperature = np.array([15, 18, 22, 25, 28, 30]).reshape(-1, 1)

# 目的変数（Y）: 売上データ - 1次元配列のままでOK
sales = np.array([3.2, 2.8, 2.1, 1.8, 1.5, 1.2])

print("データの確認:")
print(f"気温データの形状: {temperature.shape}")  # (6, 1)
print(f"売上データの形状: {sales.shape}")        # (6,)
print(f"データ点数: {len(temperature)}個")

なぜreshape(-1, 1)が必要？

scikit-learnの仕様：説明変数は2次元配列（行×列）で渡す必要がある
-1は「自動計算」の意味で、この場合6行1列になる
複数の説明変数がある場合は自然に2次元になるが、1変数の場合は明示的に変換が必要

次に、実際に回帰分析を実行します。

python

# 回帰分析の実行
# 1. モデルの作成
model = LinearRegression()

# 2. モデルの学習（データからパラメータを推定）
model.fit(temperature, sales)

print("学習完了！モデルが気温と売上の関係を学習しました")

fit()で何が起きている？

最小二乗法により、データに最もよく合う直線の傾きと切片を計算
scikit-learnのLinearRegressionは正規方程式（通常解）で最小二乗解を直接計算
学習後、model.coef_（係数）とmodel.intercept_（切片）にパラメータが保存される

学習結果を確認してみましょう。

python

# 結果の解釈
print("\n=== 回帰分析の結果 ===")
print(f"係数（傾き）: {model.coef_[0]:.3f}")        # 傾き
print(f"切片: {model.intercept_:.3f}")              # 切片  
print(f"決定係数（R²）: {model.score(temperature, sales):.3f}")  # R²

print("\n=== 結果の意味 ===")
print(f"• 気温が1℃上がると、売上が{abs(model.coef_[0]):.3f}万円下がる（係数が負のため）")
print(f"• 気温0℃のときの理論上の売上は{model.intercept_:.3f}万円")
print(f"• モデルは売上変動の{model.score(temperature, sales)*100:.1f}%を説明できる")

－各指標の解釈－

係数（傾き）: Xが1単位変化したときのYの変化量
切片: X=0のときのYの値（ただし外挿値なので解釈に注意）
決定係数（R²）: -∞～1の値で、1に近いほどモデルの説明力が高い（悪いモデルでは0未満になることもある）

最後に、学習したモデルを使って予測を行います。

python

# 予測（データ範囲内での予測推奨）
new_temp = 27  # 測定範囲内（15-30℃）での予測

# predict()メソッドは2次元配列を期待するため[[]]で囲む
predicted_sales = model.predict([[new_temp]])

print(f"\n=== 予測結果 ===")
print(f"気温{new_temp}℃のとき、予想売上: {predicted_sales[0]:.2f}万円")

# 予測の信頼性チェック
data_range = f"{temperature.min()}℃ ～ {temperature.max()}℃"
print(f"※この予測はデータ範囲内（{data_range}）なので信頼性が高いです")

# 複数の気温での予測例
test_temps = [[20], [24], [29]]
predictions = model.predict(test_temps)
print(f"\n=== 複数予測の例 ===")
for temp, pred in zip([20, 24, 29], predictions):
    print(f"気温{temp}℃ → 予想売上{pred:.2f}万円")

予測時の注意点

データの範囲外（外挿）での予測は精度が大きく下がる可能性がある
この例では15-30℃の範囲内での予測を推奨
実務では新しいデータでの検証も重要

可視化

データと回帰結果を視覚的に確認することで、モデルの妥当性を判断できます。

python

# グラフ描画の設定
plt.figure(figsize=(10, 6))  # 図のサイズを指定（幅10インチ、高さ6インチ）

# 実際のデータポイントを散布図で表示
plt.scatter(temperature, sales, 
           color='blue',           # 点の色
           label='実際のデータ',    # 凡例用のラベル
           s=100,                  # 点のサイズ
           alpha=0.7)              # 透明度

# 回帰直線を描画（滑らかな線を描くため連続値で描画）
x_smooth = np.linspace(temperature.min(), temperature.max(), 100).reshape(-1, 1)
y_smooth = model.predict(x_smooth)
plt.plot(x_smooth, y_smooth, 
         color='red',              # 線の色
         label='回帰直線',         # 凡例用のラベル
         linewidth=2)              # 線の太さ

# グラフの詳細設定
plt.xlabel('気温(℃)', fontsize=12)
plt.ylabel('売上(万円)', fontsize=12)
plt.title('カフェの売上と気温の関係', fontsize=14, fontweight='bold')
plt.legend(fontsize=11)           # 凡例を表示
plt.grid(True, alpha=0.3)         # 薄いグリッドを表示
plt.tight_layout()                # レイアウトを自動調整

# 追加情報をテキストで表示
textstr = f'y = {model.coef_[0]:.3f}x + {model.intercept_:.3f}\nR² = {model.score(temperature, sales):.3f}'
plt.text(0.05, 0.95, textstr, 
         transform=plt.gca().transAxes,  # 座標系を図の相対位置に設定
         fontsize=10,
         verticalalignment='top',
         bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))

plt.show()

実際にこのコードを実行したら・・

－可視化のポイント－

散布図 : 実際のデータの分布を確認
回帰直線 : モデルが学習した関係を可視化
R²の確認 : 直線がデータにどの程度合っているかを数値で確認
外れ値の発見 : グラフで異常な点がないかチェック

この可視化により、以下のことが分かります。

データが概ね直線関係にあるか
外れ値（大きく外れた点）があるか
等分散性（誤差が一定か）が保たれているか
モデルが適切にフィットしているか

－良いモデルの特徴－

データ点が回帰直線の周りに均等に分布
特定の範囲で誤差が大きくなっていない
R²が高い（ただし適切なしきい値は分野や目的に依存：物理実験では0.95以上、社会科学では0.3でも有用な場合がある）

注意！統計的検定について

scikit-learnは係数の統計的有意性（p値など）を提供しません
より詳細な統計分析が必要な場合はstatsmodelsライブラリを使用することを推奨します
データの範囲外（外挿）での予測は精度が大きく下がる可能性がある
この例では15-30℃の範囲内での予測を推奨
実務では新しいデータでの検証も重要

【注意点】データとの向き合い方

1. 相関関係と因果関係の違い

＜相関関係＞
一緒に変動する

＜因果関係＞
片方が原因で片方が結果

例：「アイスクリームの売上と熱中症患者数は相関がある」

相関関係 : ✓ どちらも気温と関係がある

因果関係 : ✗ アイスが熱中症の原因ではない

2. 外れ値の影響

1つの極端な値が、線全体を大きく歪める可能性があります。

＜検出方法＞

Z-score法: 平均から標準偏差の3倍以上離れた値
IQR法: 四分位範囲の1.5倍を超える値
散布図での視覚的確認

＜対策＞

データを可視化して確認
外れ値の原因を調査
必要に応じて除外や調整
ロバスト回帰（RANSAC等）の使用を検討

3. 過学習に注意！！

複雑な曲線ほど、訓練データにはよく合いますが、新しいデータでは予測が外れやすくなります。

＜バランスが重要＞

シンプルすぎる：重要な関係を見逃す
複雑すぎる：ノイズまで学習してしまう

＜対策＞

交差検証による汎化性能の確認
正則化（Ridge, Lasso回帰）の適用
AIC/BICによるモデル比較

【評価指標】「良い線」かどうかの判断

1. 決定係数（R²）

意味 : データの変動をどの程度説明できるか
範囲 : −∞〜1（0 未満は“平均だけで予測”より悪い状況）
注意 : 多変量回帰や非線形回帰では解釈が変わる場合があります

python

from sklearn.metrics import r2_score

r2 = r2_score(sales, model.predict(temperature))
print(f"決定係数: {r2:.3f}")

※単純比較なら R²、複数モデルなら adjusted R² / AIC / BIC で総合判断

2. モデル比較指標

AIC（赤池情報量規準）

モデルの複雑さを考慮した評価指標
小さいほど良いモデル

調整済み決定係数（Adjusted R²）

変数の数を考慮したR²
多変量回帰でのモデル比較に有効

2. 平均二乗誤差（MSE）

意味 : 予測値と実際の値の差の大きさ
特徴 : 小さいほど良い

python

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(sales, model.predict(temperature))
print(f"平均二乗誤差: {mse:.3f}")

3. 平均絶対誤差（MAE）

意味 : 予測値と実際の値の差の絶対値の平均
特徴 : 解釈しやすい

python

from sklearn.metrics import mean_absolute_error

mae = mean_absolute_error(sales, model.predict(temperature))
print(f"平均絶対誤差: {mae:.3f}")

4. 交差検証による汎化性能の確認

意味: モデルが新しいデータに対してどの程度予測できるかを評価
特徴: 過学習を防ぎ、モデルの汎化性能を客観的に測定

python

from sklearn.model_selection import cross_val_score

# 5分割交差検証
cv_scores = cross_val_score(model, temperature, sales, cv=5, scoring='r2')
print(f"交差検証スコア: {cv_scores.mean():.3f} (+/- {cv_scores.std() * 2:.3f})")

実用的な活用例

ビジネス場面

＜売上予測＞

過去の売上データから将来を予測
季節性、トレンドを考慮

＜価格設定＞

価格と売上の関係を分析
利益を最大化する価格を決定

＜在庫管理＞

需要予測による適切な在庫量の決定

個人的な活用

＜健康管理＞

運動量と体重の関係を分析
睡眠時間と体調の関係を把握

＜投資判断＞

経済指標と株価の関係を分析
リスクとリターンの関係を理解

＜学習効率＞

勉強時間と成績の関係を分析
効率的な学習方法を見つける

まとめ

近似曲線・最小二乗法・回帰分析は、一見複雑に見えますが、本質は「データの中にある関係性を見つけて、将来を予測する」ことです。思った以上に身近でシンプルで面白いと思いませんか？

重要なポイント

前提条件の確認 - 線形性・独立性・等分散性・正規性
データの可視化から始める - まずグラフで関係を確認
適切なモデルを選ぶ - 直線か曲線か、複雑さのバランス
汎化性能を検証 - 交差検証で過学習を防ぐ
結果を解釈する - 数値の意味を理解し、実務に活用
限界を理解する - データの範囲内での予測、相関≠因果

非エンジニアであっても、現代のツールを使えば、計算は自動でできます。重要なのは、結果を正しく解釈し、意思決定に活用する ことです。

身の回りのデータを使って、ぜひ実践してみてください。きっと新しい発見があるはずです！

この記事は、統計学の基礎知識がない方でも理解できるよう、実用性を重視して書きました。より高度な理論については、専門書籍や論文を参照してください。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

近似曲線入門 - 最小二乗法と回帰分析をやさしく理解する

はじめに

近似曲線とは「データの中にある物語を見つけること」

身近な例 → カフェの売上分析

最小二乗法 - 「一番いい線」を見つける方法

なぜ「二乗」なのか？

直感的な理解

回帰分析 - 関係性を数値で表現する

回帰分析とは

回帰分析で分かること

実際の解釈例

【種類別】 どの線を選ぶか

1. 直線（線形回帰）

2. 非線形回帰

対数・指数回帰

多項式回帰

【実践】Pythonで簡単実装

基本的な線形回帰

可視化

【注意点】データとの向き合い方

1. 相関関係と因果関係の違い

2. 外れ値の影響

3. 過学習に注意！！

【評価指標】「良い線」かどうかの判断

1. 決定係数（R²）

2. モデル比較指標

2. 平均二乗誤差（MSE）

3. 平均絶対誤差（MAE）

4. 交差検証による汎化性能の確認

実用的な活用例

ビジネス場面

個人的な活用

まとめ

【種類別】どの線を選ぶか