なにをするの？

待ち行列について簡単に説明し、Pythonのプログラムを通してシミュレーションし確認します。

待ち行列とは

確率的に挙動するシステムの混雑現象を
数理モデルを用いて解析するための理論。
オペレーションズ・リサーチの1分野。

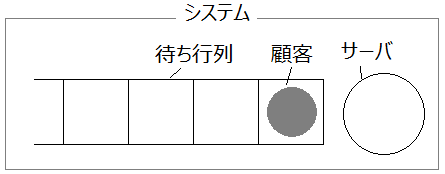
待ち行列では、サービスを提供するものをサーバ、サービスを提供されるものを顧客(クライアント)とよぶことにします。
顧客は、確率的(または確定的)に発生し、FIFO(First In First Out:先入れ先出し)の行列に並びます。
そして、先頭から確率的(または確定的)な時間をかけてサービスを受け、サービス終了後に抜けていきます。
このようなしくみを系またはシステムとよびます。

待ち行列における最も簡単なモデルは、M/M/1 モデルになります。

M/M/1 モデルとは

待ち行列では、(A)どのように到着するか、(B)どのようにサービスされるか、(C)サーバがいくつあるかが重要になります。
この3つの情報を、A/B/Cのように書く形式をケンドールの記号とよびます。つまり、M/M/1とは、以下のシステムを指します。

到着過程 = M ：ポアソン到着(おおざっぱに言えばランダムに到着すること)
サービス = M ：サービス時間が指数分布
サーバ数 = 1 ：サーバが1台

Mはマルコフ(Markov)の略で、間隔が指数分布だと到着数はポアソン分布になり、挙動はマルコフ過程になります。

待ち行列におけるパラメータ

λ(ラムダ)：平均到着率 = 単位時間¹に到着する顧客数の平均(平均到着間隔の逆数)
μ(ミュー)：平均サービス率 = 単位時間にサービスが終了する顧客数の平均(平均サービス時間の逆数)

これらのパラメータを使って以下のように計算したρは、サーバの平均稼働率になることが計算できます(後述)。

ρ(ロー)： = $ \frac{\lambda}{\mu} $

待ち行列における統計値

平均システム内人数($L$)：システム内にいる人数の期待値
平均待ち行列長($L_q$)：待ち行列に並んでいる人数の期待値
平均システム内時間($W$)：システム内に滞在している時間の期待値
平均待ち時間($W_q$)：待ち行列に並んでいる時間の期待値

待ち行列における重要な式

リトルの公式

リトルの公式とは、安定なシステムにおいて長時間平均化した顧客数$L$は、長時間平均化した到着率$λ$と、長時間平均化したシステム内時間$W$の積に等しいという法則です。(システムを待ち行列にしても同じ)

$$L = \lambda W$$
$$L_q = \lambda W_q$$

この公式は、到着分布やサービス分布がどのようなものであっても成り立ちます。
また、この式は、直感的にもわかりやすいです。すなわち、

総合病院は、経験的に、1時間に3人やってくる。また、待合室には平均6人待っていることが分かっている。
平均待ち時間は、2時間と考えられる。

これは、$W_q = L_q / \lambda = 6 / 3 = 2$ を計算したことになります。この計算は、平均について成り立ちます。
「自分が到着したとき6人並んでいた」場合の待ち時間の期待値は、(サービスがMの場合)6×平均サービス時間になります。

統計値の理論値

M/M/1では、比較的簡単に統計値の理論値を求めることができます。理論値を丸暗記しなくても、次の2つを覚えれば計算できます。

システム内人数の確率は、1人増えるとρ倍になる(マルコフ過程より導かれる)
リトルの公式

まず、システム内に$i$人いる確率$P_i$は(1)から$\alpha \rho^i$となります。確率を全て足すと1なので、下記のように計算できます。

$$ \alpha(1 + \rho + \rho^2 + \rho^3 + \cdots) = \frac{\alpha}{1 - \rho} = 1 から \alpha = 1-\rho$$
$$ システム内にi人いる確率P_i = (1-\rho) \rho^i $$

これを使うと、サーバの平均稼働率=$\sum_{i=1}{P_i} = 1 - P_0 = 1 - (1-\rho) = \rho$ということもわかります。

また、リトルの公式も使って以下のように計算できます。

平均システム内人数($L$) = $\sum_{i=0}{i P_i} = (1-\rho)(\rho+2 \rho^2 + 3 \rho^3 + \cdots) = \frac{\rho}{1-\rho}$
平均待ち行列長($L_q$) = $平均システム内人数 - サーバの平均稼働率 = L - \rho = \frac{\rho^2}{1-\rho}$
平均システム内時間($W$) = $L / \lambda = \frac{1}{\mu - \lambda}$
平均待ち時間($W_q$) = $L_q / \lambda = \frac{\rho}{\mu - \lambda}$

Pythonで確認

待ち行列シミュレーションは、Pythonの$\mbox{simpy}$を使うと便利です。インストールは、"pip install simpy"でできます。
到着率λ=1/5、サービス率μ=1/3とします。

python3

import simpy, random, numpy as np
random.seed(1)
env = simpy.Environment() # シミュレーション環境
queue, intime = [], [] # 待ち行列(到着時間のリスト) と システム内時間のリスト

# 到着イベント
def arrive():
    while True:
        yield env.timeout(random.expovariate(1.0 / 5)) # 平均到着率 1/5
        env.process(into_queue())

# 待ち行列に並ぶ
def into_queue():
    global queue
    queue.append(env.now)
    if len(queue) > 1:
        return
    while len(queue) > 0:
        yield env.timeout(random.expovariate(1.0 / 3)) # 平均サービス率 1/3
        tm, queue = queue[0], queue[1:]
        intime.append(env.now - tm)

# 実行
env.process(arrive())
env.run(1000000)
print('total = %d clients, W = %.2f' % (len(intime), np.average(intime)))
>>>
total = 199962 clients, W = 7.53

理論値は、$W = \frac{1}{\mu - \lambda} = \frac{1}{\frac{1}{3} - \frac{1}{5}} = 7.5$で、おおよそ合っているのが確認できます。

以上

単位時間とは、基準となる時間で1時間でも1分でも、モデル作成者が好きなものを決めることができます。 ↩