典型問題と実行方法の[最大流問題](http://qiita.com/Saito
Tsutomu/items/80e70da6717acacefa00)と双対関係にあり、最大フロー最小カット定理が成り立つ
最小カット問題
グラフ$G=(V,E)$の最大流に対し、始点$v_s \in V$(ソース)と終点$v_t \in V$(シンク)を分ける2つのグループを考え、両端が両グループに属する辺の流量の和が最小となるグループ分け(カットとよぶ)を求めよ。
実行方法
usage
Signature: nx.minimum_cut(G, s, t, capacity='capacity', flow_func=None, **kwargs)
Docstring:
Compute the value and the node partition of a minimum (s, t)-cut.
python
# CSVデータ
import pandas as pd, networkx as nx
from ortoolpy import graph_from_table, networkx_draw
tbn = pd.read_csv('data/node0.csv')
tbe = pd.read_csv('data/edge0.csv')
g = graph_from_table(tbn, tbe)
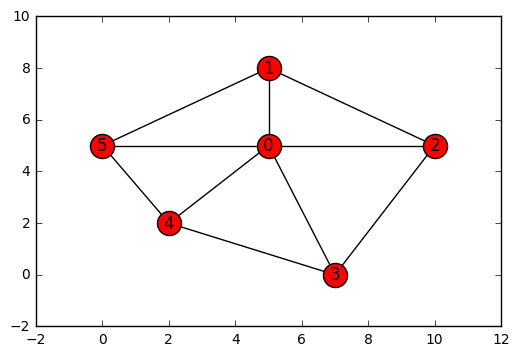
networkx_draw(g)
nx.minimum_cut(g, 5, 2)
>>>
(6, ({0, 1, 3, 4, 5}, {2}))
ノード2とそれ以外で分けられて、最小カットは6となる。
python
# 乱数データ
import networkx as nx, matplotlib.pyplot as plt
from ortoolpy import networkx_draw
g = nx.random_graphs.fast_gnp_random_graph(10, 0.3, 1)
for i, j in g.edges():
g.adj[i][j]['capacity'] = 1
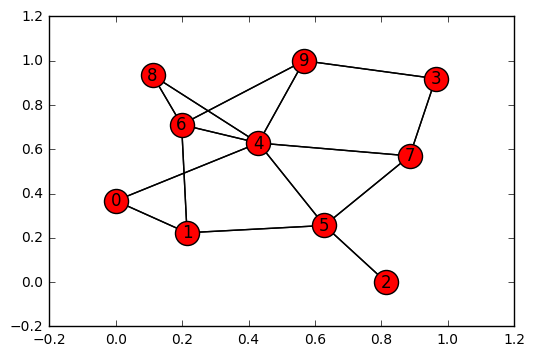
pos = networkx_draw(g, nx.spring_layout(g))
nx.draw_networkx_edges(g, pos)
nx.minimum_cut(g, 5, 6)
>>>
(3, ({2, 5}, {0, 1, 3, 4, 6, 7, 8, 9}))