測定データの選択

これなに

あなたは、メーカーの検査技師だ。あるセンサーから得られた、100個の計測データを持っている。
諸事情により、この計測データが、「ばらつく可能性があること」を示したい。
100個の中から10個を選び、分散を最大化したい。
ただし、センサーが正常であることは言いたいので、「平均値は正確」になるようにしたい。

Pythonでやってみる

測定データ作成

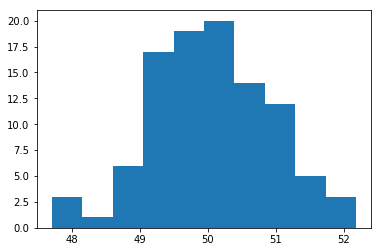
乱数で測定データを作成する。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np, pandas as pd
np.random.seed(1)
測定データ = np.random.normal(50,1,100)
plt.hist(測定データ)
print('標準偏差', 測定データ.std())
>>>
標準偏差 0.885156213832

数理最適化で解く

分散を最大化しよう。通常だと、2次整数最適化になり解きづらい。
平均値は正確だと仮定すると、$(値ー平均)^2$は、固定値になるので、モデルは、線形すなわち混合整数最適化となる。

from pulp import *
from ortoolpy import addbinvars
選択数 = 10
eps = 0.0001

m = LpProblem(sense=LpMaximize)
x = addbinvars(len(測定データ))
m += lpDot((測定データ-50)**2, x)
m += lpSum(x) == 選択数
e = lpDot(測定データ, x) / 選択数
m += 50-eps <= e
m +=           e <= 50+eps
m.solve()
%time m.solve() # 求解
r = np.vectorize(value)(x).astype(int) # 結果
print(LpStatus[m.status])
>>>
Wall time: 181 ms
Optimal

print('平均', 測定データ[r>0].mean())
print('標準偏差', 測定データ[r>0].std())
>>>
平均 49.9999119632
標準偏差 1.82811635001

平均は正確で、標準偏差は元の倍以上のデータを選択できた。

以上