N-Queen(将棋版)

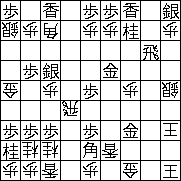
N-Queen を将棋でやってみる

駒は 敵味方20個ずつ、合計40個置くことにする。(もっと置けるかもしれないが)
条件は、どの駒も、敵味方含めて移動できる位置にいないこと。数理最適化で解いてみよう

python3

import numpy as np
from itertools import product
from more_itertools import pairwise
from pulp import *
koma = '歩90g,香21g,桂20ce,銀20fghln,金20fghikm,角21fhln,飛21gikm,王20fghiklmn'.split(',')
arr,pos,whc = [],[0],[]
for iko, ko in enumerate(koma):
    for my in range(-1,2,2):
        ar = []
        lst = [(ord(c)%3-1,(ord(c)//3-35)*my) for c in ko[3:]]
        for x,y in product(range(9),range(9)):
            a = [0]*81
            a[x+y*9] = 40
            for p,q in lst:
                for z in range(1,int(ko[2])*7+2):
                    i,j = x+z*p,y+z*q
                    if not (0<=i<9 and 0<=j<9):
                        break
                    a[i+j*9] = 1
            ar.append(a)
        arr.extend(ar)
        pos.append(pos[-1]+len(ar))
        whc.extend([iko*2+my//2+1]*len(ar))
        if iko > 4:
            break
A = np.array(arr)
pp = (A==40).dot(range(81))

m = LpProblem()
x = [LpVariable('x%.4d'%i, cat=LpBinary) for i in range(A.shape[0])]
m += lpSum(x) == 40
for i, (p1, p2) in enumerate(pairwise(pos)):
    m += lpSum(x[p1:p2]) <= int(koma[i//2 if i < 10 else i-5][1])
for i in range(81):
    m += lpDot(x,A[:,i]) <= 40
%time m.solve(GUROBI_CMD())
print(LpStatus[m.status])
>>>
Wall time: 582 ms
Optimal

さすが、GUROBI！
0.5秒ほどで解けた¹。

表示してみよう。

python3

from PIL import Image, ImageDraw, ImageFont
v = np.vectorize(value)(x)
n = 181
fnt = ImageFont.truetype(r'C:\Windows\Fonts\ipaexg.ttf', 18)
im = Image.new(mode='1', size=(n,n), color=1)
for h in range(2):
    im = im.transpose(Image.ROTATE_180)
    d = ImageDraw.Draw(im)
    d.font = fnt
    for i,j,k in zip(range(40),np.array(whc)[v==1],pp[v==1]):
        x,y = (k%9,k//9) if h else (8-k%9,8-k//9)
        if (j<=9 and j%2==h) or (j>9 and i%2==h):
            d.text((x*20+2,y*20+2),koma[j//2][0])
for i in range(10):
    d.line([(0,i*20),(n,i*20)])
    d.line([(i*20,0),(i*20,n)])
im.show()

参考:

• 組合せ最適化でN Queen問題を解く - Qiita

以上

1. 「目的関数が dummy の許容性判定問題となっています．『線形緩和問題の許容解の目的関数値＝元問題の最適値』なので，整数許容解が見つかった瞬間に分枝が終了します．」農工大の宮代先生のコメントより ↩