数理最適化による問題解決について説明し、巡回セールスマン問題を例に実際にPythonでモデル化の例を紹介します。
数理最適化とは
数理最適化とは、問題解決の手法です。
課題を数理モデルとしてとらえ、最適解(最も良い答え)を求めます。ここでは最適解を1つだけ求めることを考えます。
数理モデルは、「変数、制約条件、目的関数」で構成されます。
変数のとりうる空間を解空間といい、1つの解は空間上の1点になります。
制約条件は、空間の中の壁になります。目的関数は、空間の中のベクトル(進行方向)になります。
すなわち、最適化とは、壁で囲まれた空間(実行可能領域)を進行方向に最も進んだ点を探すことです。
社会の最適化問題
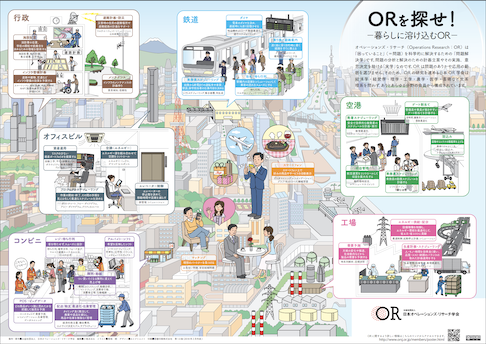
数理最適化は、社会の問題解決に役立っています。ここでは、オペレーションズ・リサーチ学会(OR学会)の「ORを探せ!」ポスターから抜粋してみます。
- 避難施設の配置計画作成
- エネルギーマネージメント計画作成
- 商品の配置最適化
- 店員のシフトスケジューリング
- 商品の配送計画の作成
- 列車の運行スケジューリング
- 列車の乗務員スケジューリング
- 駅の乗り換えの最適化
- 物流コンテナのパッキング
- 生産計画の作成
- 在庫計画の作成
最適化問題の種類
よく使われる最適化問題に、線形最適化問題と混合整数最適化問題があります。
- 線形最適化問題は、進行方向の壁にぶつかったら、壁に沿って進むことで最適解が簡単に見つかります。
- 混合整数最適化問題は、空間がつながっていないことがあるので、最適解を見つけることが難しくなります。しかし、最近では比較的簡単に解けるようになってきました。ただし、壁が曲面になる非線形最適化問題は、解けないことが多いです。
混合整数最適化問題の例としては、巡回セールスマン問題があります。これは、「複数の都市を最も早く全都市を回る順番を求める問題」です。
参考:巡回セールスマン問題の書籍
- 驚きの数学 巡回セールスマン問題:ウィリアム・J・クック (著), 松浦俊輔 (翻訳)
- 巡回セールスマン問題への招待:山本 芳嗣 (著), 久保 幹雄 (著)
- グラフ理論の魅惑の世界- 巡回セールスマン問題、四色問題、中国人郵便配達問題:アーサー・ベンジャミン 他(著)
巡回セールスマン問題の応用例
巡回セールスマン問題の応用例は、以下のように色々あります。
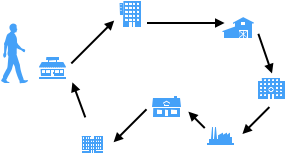
- コンビニや自動販売機などの商品の補充
- 複数台の車両を用いた配送最適化問題の部分問題
- ばらばらのアイテムを元通りに戻す(つながりやすさを距離と考える)
- 最短超文字列問題(後述)
最短超文字列問題とは
ここからは、具体的な問題を例に、モデル化の妙を見ていきます。
以下のような最短超文字列問題を考えます。
入力:文字列の集合S
出力:S中のすべての文字列を部分文字列として含む最短の文字列の長さ
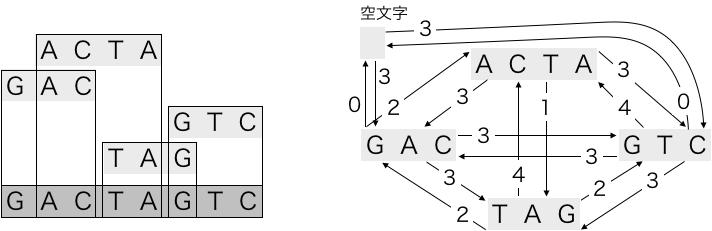
たとえば、S = ['TAG', 'ACTA', 'GTC', 'GAC'] ならば、最短超文字列は GACTAGTCになります。
参考:「涼宮ハルヒの憂鬱」のおかげで25年解けなかった数学の難問が解決されるかもしれない
解いてみよう
文字列の集合から部分文字列となるものを除いて、空文字列("")を追加しておきます。
文字列間の距離を伸びる長さとすれば、最短超文字列問題は、巡回セールスマン問題そのものです。
例えば、GACからACTAへは、伸びる長さは2です。伸びる長さは「2つの文字列の長さの和から重なる長さを引いたもの」です。
まずは、2つの文字列の重なる長さを求める関数を定義します。
def overlap(s,t):
"""sとtの重なりの長さ"""
m = len(s)
n = max(0, m-len(t))
for i in range(n,m):
if s[i:] == t[:m-i]:
return m-i
return 0
print(overlap('12345' , '3456')) # 3
print(overlap('1234' , '12345')) # 4
print(overlap('1234' , '2345')) # 3
巡回セールスマン問題は、ortoolpy.tspを使って解きましょう(厳密解を求めているので規模が大きくなると解けなくなるので注意してください)。
from ortoolpy import tsp
def shortest_superstring(words):
"""最短超文字列問題"""
words = [''] + words
n = len(words)
dist = {(i, j): len(t) - overlap(s, t)
for i, s in enumerate(words)
for j, t in enumerate(words) if i != j}
_, lst = tsp(words, dist)
return ''.join(words[j][len(words[j]) - dist[i, j]:]
for i, j in zip(lst, lst[1:]))
print(shortest_superstring(['TAG', 'ACTA', 'GTC', 'GAC'])) # GACTAGTC
GACTAGTCと出力されます。解くことができました。
社会には様々な問題がありますが、典型的な問題に帰着させて考えると解きやすくなります。
参考
以上