2つの封筒問題をGeminiに質問したところ、珍しくシンプルに間違えてました。
本記事では、その間違いを指摘します。なお、金額は自然数とします。
問題
お金の入った2つの封筒があり、片方はもう一方の2倍の金額になっている。無作為に1つの封筒を選んだとき、交換した方が得か?
Geminiによる間違った回答
封筒を交換する方が得になる可能性が高いです。
以下に詳しく説明します。
選んだ封筒に入っている金額をxとします。このとき、もう一方の封筒に入っている金額は2xかx/2のいずれかになります。
それぞれのケースの確率は1/2です。
(中略)
交換した場合に得られる金額の期待値を計算してみましょう。
(中略)
期待値 =5x/4
これは、最初に選んだ封筒に入っている金額xよりも大きい値です。したがって、期待値の観点からは、封筒を交換する方が得であると言えます。
解説
正解は「交換しても期待値は変わらない」です。
Geminiは何を間違えたのか
Geminiの回答の間違いポイントは2つあります。
- 金額を分布でなく1つの値としたこと
-
2xかx/2の確率を半々としたこと
具体例で考えてみましょう。
| 2つの封筒の値 | そのペアになる確率 |
|---|---|
| (1, 2) | p1 |
| (2, 4) | p2 |
| (3, 6) | p3 |
| (4, 8) | p4 |
| 続く |
片方の金額をxとしたとき、そのxはいろいろな値が考えられます。それらの値がどの確率で現れるかを下記のようにすべて考慮しないといけません。
- 確率
p1/2でxは1 - 確率
p1/2 + p2/2でxは2 - 確率
p3/2でxは3 - 確率
p2/2 + p4/2でxは4 - 続く
また、xが2のとき、もう一方が4か1になる確率は半々ではありません。割合はp2/2とp1/2です。
p1、p2、p3、p4は、問題に明記されていないので、わかりません。
また、半々になるような分布は存在しません。
どう考えればよかったのか
交換したときの差分の期待値が0になることを示せば「交換しても期待値は変わらない」が言えます。
この期待値は下記で計算できます。
$$ 期待値 = \sum_{i=1}^{\inf}{ p_i (\frac{i - 2i}{2} + \frac{2i - i}{2}) } $$
任意の$i$に対して$p_i (\frac{i - 2i}{2} + \frac{2i - i}{2})$が0なので、分布に関係なく期待値は0です。
補足
確率分布に従って値が決まるものを確率変数といいます。確率変数は一般にXのように大文字で表現します。
今回の場合、片方の値はxではなくXのように確率変数で考えるべきでした。
別の考え方
2つの値になる確率を次図のように考えます。
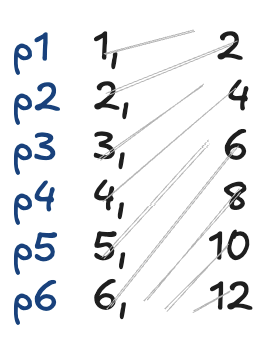
片方をyとし、もう一方をzとすると、上図は下表のようになります。
| y | 確率 | z |
|---|---|---|
| 1 | p1/2 | 2 |
| 2 | p1/2 | 1 |
| 2 | p2/2 | 4 |
| 3 | p3/2 | 6 |
| 4 | p2/2 | 2 |
| 4 | p4/2 | 8 |
| 5 | p5/2 | 10 |
| 6 | p3/2 | 3 |
| 6 | p6/2 | 12 |
| 8 | p4/2 | 4 |
| 10 | p5/2 | 5 |
| 12 | p6/2 | 6 |
この表のyの期待値とzの期待値は同じ値になります。したがって、封筒を交換したときの期待値は変わりません。
以上