これなに
日本地図を県別に色分けする Python3 用のライブラリ(japanmap)を作成したので紹介します。
実行例は、Jupyter Notebook 上で確認しています。
インストール
pipでできます。numpy1、OpenCV、Pillowも一緒にインストールされます。xlrdは、Excelファイルの読み込みで使います。
pip install -U japanmap jupyter matplotlib pandas xlrd
県コードとは
都道府県コード(以下、県コードと略す)は、JIS X 0401 により定められた、各都道府県ごとの01から47のコードです。
プログラムでは整数で扱います（頭の0を無視します）。
県名確認
pref_namesで県コードごとの県名がわかります。
from japanmap import pref_names
pref_names[1]
>>>
'北海道'
pref_codeで県名に対する県コードがわかります。
from japanmap import pref_code
pref_code('京都'), pref_code('京都府')
>>>
(26, 26)
groupsで八地方区分ごとの県コードがわかります。
from japanmap import groups
groups['関東']
>>>
[8, 9, 10, 11, 12, 13, 14]
白地図
pictureで白地図(ラスタデータ)を取得できます。
%config InlineBackend.figure_formats = {'png', 'retina'}
%matplotlib inline
import matplotlib.pyplot as plt
from japanmap import picture
plt.rcParams['figure.figsize'] = 6, 6
plt.imshow(picture());
県を色で塗ることもできます。
plt.imshow(picture({'北海道': 'blue'}));
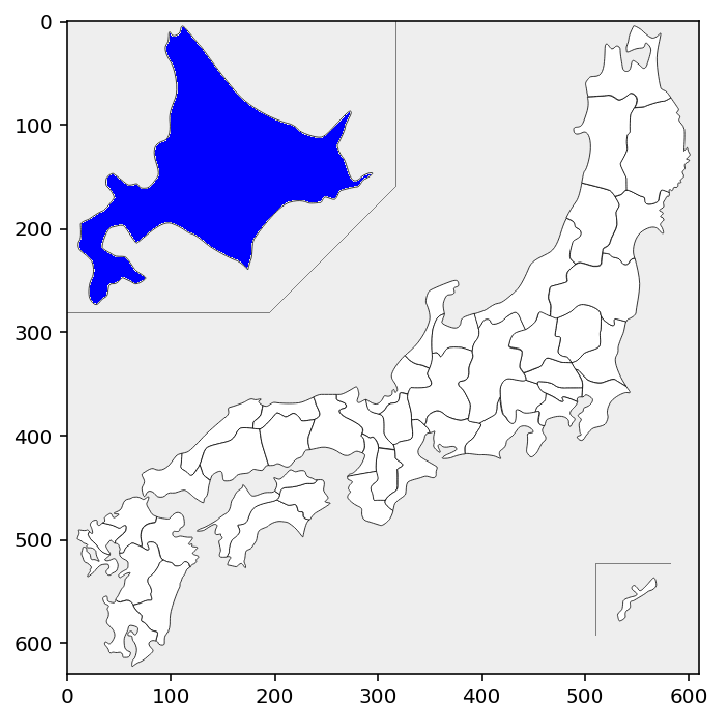
PNGファイルへの保存
savefigでファイルに保存できます。
plt.imshow(picture({'北海道': 'blue'}))
plt.savefig('japan.png')
隣接情報
is_faced2sea で県コードに対して、庁所在地を含むエリアが海に面しているかわかります。
from japanmap import is_faced2sea
for i in [11, 26]:
print(pref_names[i], is_faced2sea(i))
>>>
埼玉県 False
京都府 True
is_sandwiched2sea で県コードに対して、庁所在地を含むエリアが海に挟まれているかわかります。(連続でない海辺が2つ以上あるか)
from japanmap import is_sandwiched2sea
for i in [2, 28]:
print(pref_names[i], is_sandwiched2sea(i))
>>>
青森県 False
兵庫県 True
adjacent で県コードに対して、庁所在地を含むエリアが隣接する県コードがわかります。
from japanmap import adjacent
for i in [2, 20]:
print(pref_names[i], ':', ' '.join([pref_names[j] for j in adjacent(i)]))
>>>
青森県 : 岩手県 秋田県
長野県 : 群馬県 埼玉県 新潟県 富山県 山梨県 岐阜県 静岡県 愛知県
境界線のベクトルデータ
get_data で各県の点リストと点のindexリストが取れます。これを使うと、pref_points で県の境界(index list)のリストが取れます。
from japanmap import get_data, pref_points
qpqo = get_data()
pnts = pref_points(qpqo)
pnts[0] # 北海道の境界座標(経度緯度)リスト
>>>
[[140.47133887410146, 43.08302992960164],
[140.43751046098984, 43.13755540826223],
[140.3625317793531, 43.18162745988813],
...
pref_map で境界線データを可視化できます。
from japanmap import pref_map
svg = pref_map(range(1,48), qpqo=qpqo, width=2.5)
svg
SVGファイルへの保存
pref_mapは、SVG形式です。下記のようにしてファイルに保存できます。
with open('japan.svg', 'w') as fp:
fp.write(svg.data)
関東だけをグレースケールにする例。
pref_map(groups['関東'], cols='gray', qpqo=qpqo, width=2.5)
県別データ(人口)を使って、県の面積比を変換
人口比で地図上の面積比を変換してみましょう。総務省統計局の「なるほど統計学園」の人口データの画面下部の「出典の統計表」を押して2017年の県別の人口2のファイル（a00400.xls）をダウンロードしましょう。
import pandas as pd
df = pd.read_excel('a00400.xls', usecols=[9, 12, 13, 14], skiprows=18, skipfooter=3,
names='都道府県 男女計 男 女'.split()).set_index('都道府県')
df[:3]
| 男女計 | 男 | 女 | |
|---|---|---|---|
| 都道府県 | |||
| 北海道 | 5320 | 2506 | 2814 |
| 青森県 | 1278 | 600 | 678 |
| 岩手県 | 1255 | 604 | 651 |
人口比の多い順に表示してみましょう。東京都の比の5.09は、県平均の5.09倍を表しています。
df['比'] = df.男女計 / df.男女計.mean()
df.sort_values('比', ascending=False)[:10]
| 男女計 | 男 | 女 | 比 | |
|---|---|---|---|---|
| 都道府県 | ||||
| 東京都 | 13724 | 6760 | 6964 | 5.090665 |
| 神奈川県 | 9159 | 4569 | 4590 | 3.397362 |
| 大阪府 | 8823 | 4241 | 4583 | 3.272729 |
| 愛知県 | 7525 | 3764 | 3761 | 2.791260 |
| 埼玉県 | 7310 | 3648 | 3662 | 2.711510 |
| 千葉県 | 6246 | 3103 | 3143 | 2.316839 |
| 兵庫県 | 5503 | 2624 | 2879 | 2.041237 |
| 北海道 | 5320 | 2506 | 2814 | 1.973356 |
| 福岡県 | 5107 | 2415 | 2692 | 1.894348 |
| 静岡県 | 3675 | 1810 | 1866 | 1.363174 |
可視化してみます。
trans_areaで県の面積を指定した比率に変換できます。
例えば、県ごとの変換比率を[2, 1, 1, 1, ...]とすると、北海道が元の面積の2倍、他県が元の面積と同じ比率になります。
下記では、人口が平均の2倍であれば面積を2倍にするように表示しています。
from japanmap import trans_area
qpqo = get_data(True, True, True)
pref_map(range(1,48), qpqo=trans_area(df.男女計, qpqo), width=2.5)
なるべく、ラフにして歪みを減らしたのですが、なかなか厳しいです。
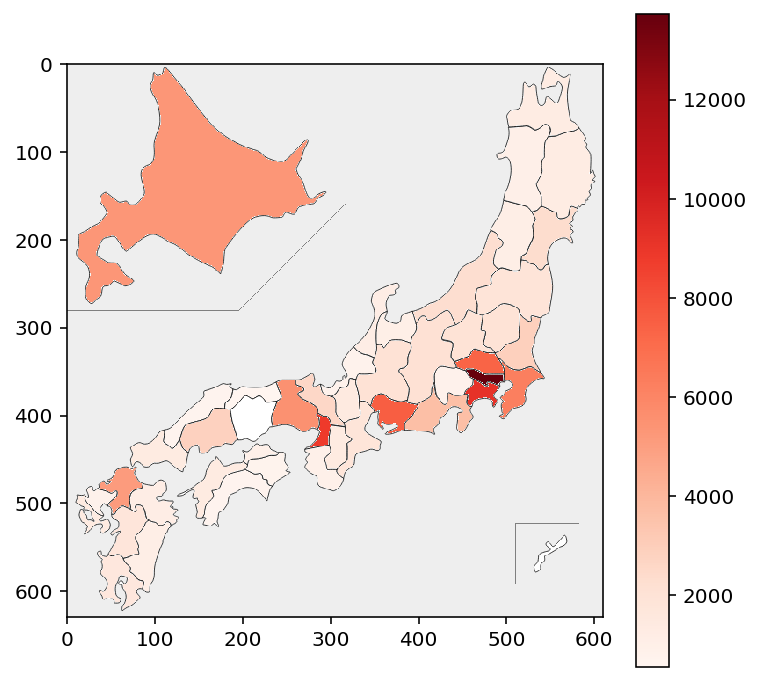
白地図上で人口を可視化
下記のようにすると、人口の多い県を濃い赤で可視化できます。
cmap = plt.get_cmap('Reds')
norm = plt.Normalize(vmin=df.男女計.min(), vmax=df.男女計.max())
fcol = lambda x: '#' + bytes(cmap(norm(x), bytes=True)[:3]).hex()
plt.colorbar(plt.cm.ScalarMappable(norm, cmap))
plt.imshow(picture(df.男女計.apply(fcol)));
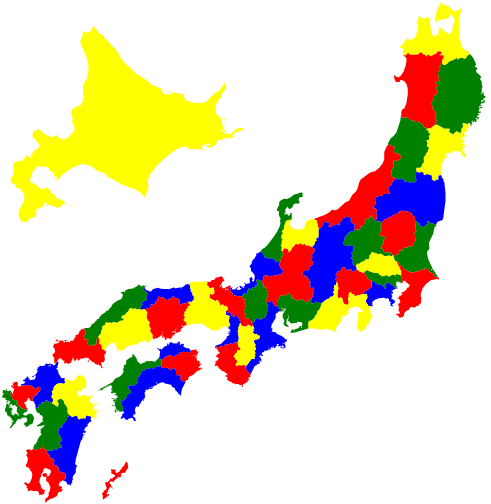
4色問題
隣接情報を使って4色問題を解いてみましょう。
1つの県を1色とし、隣接する県は異なるように、日本全体を4色で塗りましょう。このように隣り合うもの同士に違う色を割当てる問題を、頂点彩色問題とよびます。
頂点彩色問題とは、グラフ上で隣接する頂点が異なる色になるように、最小の色数で頂点に色を割り当てる問題です。
この応用としては、例えば、携帯電話の基地局ごとの周波数を決める問題があります。(異なる色→異なる周波数→電波が干渉しないので話せる)
4色問題を解く
どのような平面地図であっても隣接するエリアが異なるようにして、必ず4色以内で塗り分けられることが、数学的に証明されています。しかし、どのように塗り分けたらよいかは、自明ではありません。ここでは、数理最適化を解いて求めることにしましょう。
数理最適化は、コストの最小化などを解くときに使われますが、目的関数がない制約だけの問題でも解くことができます。数理最適化で用いるパッケージ PuLPについては、最適化におけるPythonを見てください。
- 数理モデル(1)で決めないといけないことは、変数表現、目的関数、制約条件の3つです。
- 変数表現： 47都道府県×4色で188個の0または1しか取らない変数を用意します。このような変数は、バイナリ変数とよばれます。 変数は、パッケージ pandasの表で管理します。この変数表(2)を使うことにより制約条件をわかりやすく書くことができます。
- 目的関数： 今回は最大化などを行いませんので、設定しません。PuLPでは、目的関数を設定しなくても実行できます。
- 制約条件： 1県ごとに1色とします(3)。隣接した県同士は、異なる色にします(4)。
- 数理モデルができたら、ソルバーを実行するだけで解を求めることができます(5)。 ソルバーは、数理モデルを解くソフトウェアで、pulpをインストールすると一緒にインストールされます。
- 結果は、変数に対してvalueをよぶことで確認できます。ここでは、変数表に、新しい列"Val"を追加し結果を設定しています(6)。 この新しい列が0でない行を取得することにより、県に対する塗るべき色がわかります。
実行するためには、追加で PuLPと ortoolpyが必要です（pip install pulp ortoolpy）。
import pandas as pd
from ortoolpy import model_min, addbinvars, addvals
from pulp import lpSum
from japanmap import pref_names, adjacent, pref_map
m = model_min() # 数理モデル(1)
df = pd.DataFrame([(i, pref_names[i], j) for i in range(1, 48) for j in range(4)],
columns=['Code', '県', '色'])
addbinvars(df) # 変数表(2)
for i in range(1, 48):
m += lpSum(df[df.Code == i].Var) == 1 # 1県1色(3)
for j in adjacent(i):
for k in range(4): # 隣接県を違う色に(4)
m += lpSum(df.query('Code.isin([@i, @j]) and 色 == @k').Var) <= 1
m.solve() # 求解(5)
addvals(df) # 結果設定(6)
四色 = ['red', 'blue', 'green', 'yellow']
cols = df[df.Val > 0].色.apply(四色.__getitem__).reset_index(drop=True)
pref_map(range(1, 48), cols=cols, width=2.5)
