組合せ最適化 - 典型問題 - 中国人郵便配達問題

典型問題と実行方法
##中国人郵便配達問題
無向グラフにおいて、全ての辺を必ず1度は通って元の点に戻る経路の中で最小になるものを求めよ。

##実行方法

usage

Signature: chinese_postman(g_, weight='weight')
Docstring:
中国人郵便配達問題
入力
    g: グラフ
    weight: 重みの属性文字
出力
    距離と頂点リスト

python

# CSVデータ
import pandas as pd, networkx as nx, matplotlib.pyplot as plt
from ortoolpy import chinese_postman, graph_from_table, networkx_draw
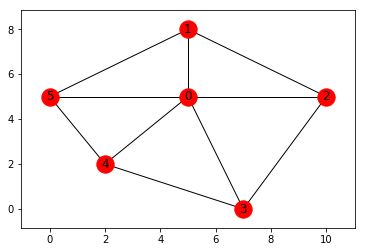
tbn = pd.read_csv('data/node0.csv')
tbe = pd.read_csv('data/edge0.csv')
g = graph_from_table(tbn, tbe, multi=True)[0]
networkx_draw(g)
plt.show()
print(chinese_postman(g))

結果

(36.0, [(0, 4), (4, 5), (5, 4), (4, 3), (3, 2), (2, 3), (3, 0),
        (0, 5), (5, 1), (1, 2), (2, 0), (0, 1), (1, 0)])

python

# pandas.DataFrame
from ortoolpy.optimization import ChinesePostman
ChinesePostman('data/edge0.csv')[1]

	node1	node2	capacity	weight
0	0	4	2	2
1	4	5	2	1
2	4	5	2	1
3	3	4	2	4
4	2	3	2	3
5	2	3	2	3
6	0	3	2	2
7	0	5	2	4
8	1	5	2	5
9	1	2	2	5
10	0	2	2	4
11	0	1	2	1
12	0	1	2	1

python

# 乱数データ
import math, networkx as nx, matplotlib.pyplot as plt
from ortoolpy import chinese_postman, networkx_draw
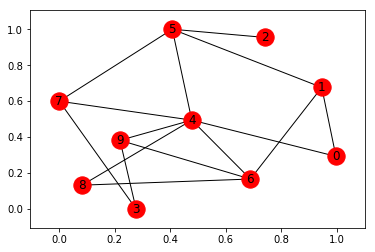
g = nx.random_graphs.fast_gnp_random_graph(10, 0.3, 1)
g = nx.MultiGraph(g)
pos = nx.spring_layout(g)
for i, j, k in g.edges:
    g.adj[i][j][k]['weight'] = math.sqrt(sum((pos[i] - pos[j])**2))
networkx_draw(g, nx.spring_layout(g))
plt.show()
print(chinese_postman(g))

結果

(7.054342373467126, [(0, 4), (4, 8), (8, 6), (6, 9), (9, 7), (7, 4),
                     (4, 9), (9, 3), (3, 7), (7, 5), (5, 4), (4, 6),
                     (6, 1), (1, 2), (2, 5), (5, 1), (1, 0)])

##データ

• data/node0.csv
• data/edge0.csv