最適化でバラバラの写真を復元せよ！

手掛かりはバラバラの写真

犯人のアジトに警察が踏み込んだところ、時すでに遅く、犯人は証拠の写真をシュレッダーにかけた後だった。
シュレッダーにかけられた短冊状の切れ端を並べ替えて、写真を復元しよう。

バラバラの写真の用意

写真を読み込む→変数ar

stocksnap.ioの写真を使います。Pythonで読み込んでみます。

python3

import numpy as np, networkx as nx, matplotlib.pyplot as plt
from PIL import Image
from urllib import request
with request.urlopen('https://snap-photos.s3.amazonaws.com/'
                     'img-thumbs/960w/X8CW5LGMWI.jpg') as fd:
    im = Image.open(fd) # 写真読込
ar = np.array(im.convert('L').getdata()) # グレー('L')にして、np.ndarrayに変換
ar = ar.reshape((im.height, -1))
plt.imshow(ar, cmap='gray'); # 表示

写真をバラバラにする→変数sp

20ピクセルごとに、横に切ってシャッフルして繋げます。

python3

wd = 20 # 短冊の幅
n = im.height // wd # 分割数
r = range(n)

sp = [ar[i*wd:(i+1)*wd] for i in r]
tmp = sp[1:]
np.random.seed(1)
np.random.shuffle(tmp)
sp = [sp[0]] + tmp # 先頭のみ同じ順番のままにし、残りシャッフル
plt.imshow(np.concatenate(sp), cmap='gray'); # バラバラの写真

考え方

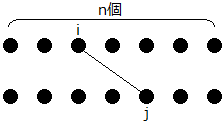
n個の短冊に対し、つながるかどうかを2部グラフで考えます。

すなわち、上のノードiと下のノードjを結んだときに、短冊iの下に短冊jを繋げることにします。
つなげたときに重みは、「短冊iの下1列のピクセルと短冊jの上1列のピクセルの差分の小さい値の50%のノルム」のマイナスとし、最小が0になるように調整します。
この2部グラフに対し、組合せ最適化問題の最大重みマッチング問題を解くことで、並べ方を求めることができます。

重みを計算する→wgt

下記のように計算します。

python3

nn = int(im.width * 0.5) # 50%を使う
t = [[np.linalg.norm(np.sort(np.abs(sp[i][-1] - sp[j][0]))[:nn])
      for j in r] for i in r]
wgt = np.max(t) - t

有向グラフを作成→g

上のノードを0...n-1とし、下のノードをn...2*n-1とします。このグラフは2部グラフです。

python3

g = nx.DiGraph() # 有向グラフ
for i in r:
    for j in r:
        if i != j:
            g.add_edge(i, j+n, weight=wgt[i][j])

解いて結果を表示します→mtc

2部グラフの最大重みマッチング問題を解きます。0から順番に結果(mtc)をたどると、つなぎ方がわかります。

python3

mtc = nx.max_weight_matching(g) # 最大重みマッチング問題を解く
# resに順番を入れる
i, res = 0, []
for _ in r:
    res.append(sp[i])
    i = mtc[i] - n
plt.imshow(np.concatenate(res), cmap='gray'); # 結果表示

一応、うまくいきました。