最短時間で道路を舗装せよ
あなたは、町役場の土木課の職員です。
- 未舗装の道路ネットワークを(人手不足なので)1人で舗装しなければいけません。
- 最後に作業開始地点に戻らないといけません。
- なるべく早く作業を終えたいとします。
考え方
全ての辺(道路)を辿る閉路(一周して戻ってくる経路)を求める問題を、中国人郵便配達問題といいます。
ワーシャルフロイド法を用いて多項式時間で計算することができますが、ここでは組合せ最適化の混合整数最適化問題と捉えて解くことにします。
連結グラフの全ての点の次数(点に接続している辺の数)が偶数であれば、閉路が存在することが知られています。次数が奇数のときは、同じ道路上を往復して偶数になるようにすればよいことになります。
方針としては、道路を往復すべきかどうかを求めることにします。
(次数が全て偶数のグラフの閉路は比較的簡単に求まりますので、ここでは省略します。)
定式化
| 最小化 | $\sum_i{x_i}$ | 往復する道路 |
| 変数 | $x_i \in \{0, 1\} ~ \forall i \in 道路$ | 往復するかどうか |
| $y_j \ge 0, \in 整数 ~ \forall j \in 点$ | 点の次数の半分 | |
| 制約条件 | $\sum_{i \in 点jに接続している辺}{~~~~~~~~~~~~ x_i + 点jの次数} = 2 y_j \forall j \in 点$ | 次数が偶数 |
(この定式化は、あまりよくないので、実際には別の方法がよいでしょう。)
Pythonで実行
ランダムなグラフを作成します。
python3
%matplotlib inline
import networkx as nx
from pulp import *
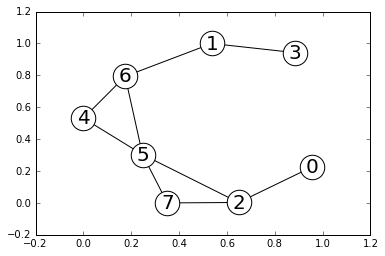
g = nx.random_graphs.fast_gnp_random_graph(8, 0.3, 11)
pos = nx.spring_layout(g)
nx.draw_networkx_nodes(g, pos=pos, node_size=600, node_color='w')
nx.draw_networkx_edges(g, pos=pos)
nx.draw_networkx_labels(g, pos=pos, font_size=20)
print([i for i, l in enumerate(g.adjacency_list()) if len(l)%2])
>>>
[0, 2, 3, 6]
点0, 2, 3, 6 の次数が奇数なので、これらの間を結べばよいことが、わかります。
定式化して解いてみます。
python3
m = LpProblem()
xs, ys = [], []
for i, j in g.edges():
g.edge[i][j]['x'] = x = LpVariable('x%d_%d'%(i,j), cat=LpBinary)
xs.append(x)
m += lpSum(xs)
for i, ad in enumerate(g.adjacency_list()):
y = LpVariable(
'y%d'%i, cat=LpInteger)
m += lpSum(g.edge[i][j]['x'] for j in ad) + len(ad) == 2 * y
ys.append(y)
m.solve()
print([g.edges()[i] for i, x in enumerate(xs) if value(x)])
>>>
[(0, 2), (1, 3), (1, 6)]
最短で、点0, 2, 3, 6 が結ばれているのがわかります。
以上