組合せ最適化で星の調査

これなに

• 光子ロケットで1列に連なる1000個の星を調査する。
• エイリアンがいないか調べよう。ただし、全ての星を調べることはできない。
• 星ごとに調査時間は異なる。調査対象の星の調査時間の総和は、10000日以内にしよう。
• 星ごとに発見確率を推定している。調査対象の星の発見確率の総和を最大化せよ。

解いてみる

ナップサック問題として、考えることができる。Pythonで解いてみよう。
Pythonによる数理最適化については、参考リンクを参照のこと。

python3

import numpy as np
from pulp import *
np.random.seed(1)
星数 = 1000
調査時間 = np.random.randint(10,100,星数)
発見確率 = np.random.random(星数)/100000
m = LpProblem(sense=LpMaximize)
x = [LpVariable('x%.4d'%i, cat=LpBinary) for i in range(星数)]
m += lpDot(発見確率,x)
m += lpDot(調査時間,x) <= 10000
m.solve()
print(value(m.objective)) # 発見確率の総和
>>>
0.0022822674119170536

実は、ロケットは、最大航続可能距離がある。ここでは、単純に距離ではなく、最大ホップ数+1をmxとする。
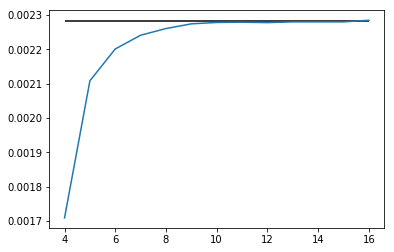
mxを変えたとき、目的関数がどうなるか見てみよう。横軸はmx、縦軸は目的関数である。

python3

r = []
for mx in range(4,17):
    m = LpProblem(sense=LpMaximize)
    x = [LpVariable('x%.4d'%i, cat=LpBinary) for i in range(星数)]
    m += lpDot(発見確率,x)
    m += lpDot(調査時間,x) <= 10000
    for i in range(星数-mx+1):
        m += lpSum(x[i:i+mx]) >= 1 # mx以内に1か所以上調査する
    m.solve()
    r.append(value(m.objective))

%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(range(4,17),r)
plt.hlines(0.0022822674119170536,4,16);

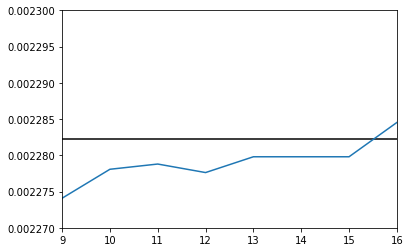
拡大してみる。

python3

plt.plot(range(4,17),r)
plt.hlines(0.0022822674119170536,4,16)
plt.xlim((9,16))
plt.ylim((0.00227,0.0023));

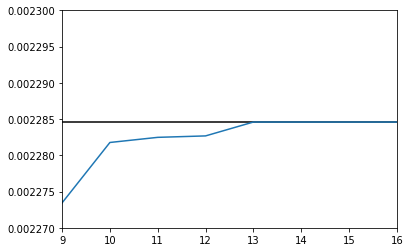
デフォルトの無料のソルバーCBCだと、誤差のせいで、制約条件が厳しい方が解がよくなったりしている。

商用ソルバーは、より正確に解けた。

参考リンク
- 最適化におけるPython - Qiita

以上