これなに
12/2 に行われた最適化のセミナー Gurobi Optimizerソリューションセミナー2016 で、学校の学区決めを多品種最小費用流問題として解けることを聞いたので実際にやってみました。
- 県別データの可視化ライブラリjapanmapを使います。
- 本州の34都府県を対象にし、1県に1人学生がいるとします。
- 青森、山梨、山口に学校があり、定員はそれぞれ 7、21、6人とします。
- 隣接県への移動時間は、1とします。
- 各学生が3つの学校のいずれかに通うこととし、全学生の総移動時間を最小化する学区の割当を求めます。
考え方
- 34都府県の需要点を作成します。
- 青森、山梨、山口の需要をそれぞれ(自分を除いた)6、20、5、その他は-1とします。
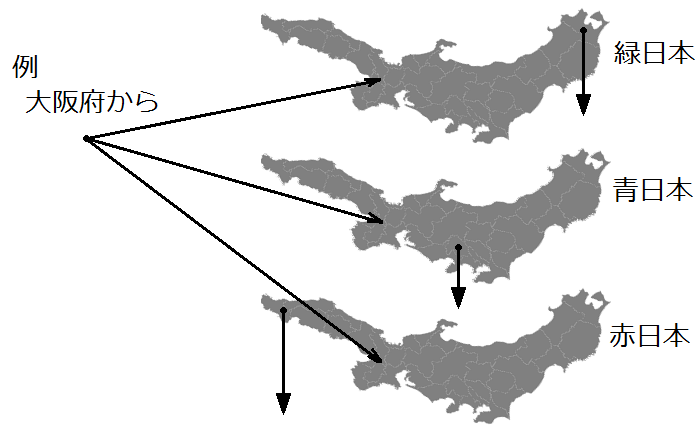
- 青森、山梨、山口を代表とする3つの日本(緑日本、青日本、赤日本)を考え、この各日本の中で隣接させます。(多品種ネットワーク)
- 代表点以外の需要点から3つの日本の同じ県にリンクをはります。
- 代表点の需要点へ、その代表点を代表とする各日本の同じ県からリンクをはります。
このネットワーク上で最小費用流問題を解きます。
Python でやってみる
python3
import numpy as np, networkx as nx
from japanmap import adjacent, pref_code, pref_map
本州 = np.arange(2,36)
代表点 = {pref_code('青森'):7, pref_code('山梨'):21, pref_code('山口'):6}
# グラフ作成
g = nx.DiGraph()
g.add_nodes_from(本州, demand=-1)
for i, d in 代表点.items():
nwl = i*100
g.node[i]['demand'] = d-1
g.add_nodes_from(nwl+本州, demand=0)
g.add_edge(nwl+i,i)
g.add_edges_from((j,nwl+j) for j in 本州 if j not in 代表点)
g.add_edges_from(((nwl+j,nwl+k) for j in 本州 for k in adjacent(j)), weight=1)
r = nx.min_cost_flow(g)
# 結果表示
dc = dict(zip(代表点,['red','green','blue']))
dc.update({i:dc[j//100]for i, t in r.items() for j, v in t.items() if v and i < 100})
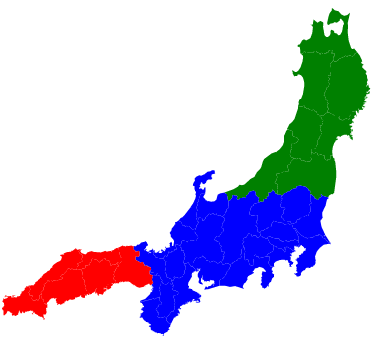
pref_map(本州, cols=[dc[i] for i in 本州], width=4)
思った通りに解けました。
発展
現実には、いろいろな要素を考慮する必要があります。
- なるべく前と同じ学区が望ましい。
- 特定のところで必ずわけたい。
- ホップ数ではなく距離にする。
- グループ内の数はぴったりでない。
定式化を直せばできそうです。
以上