最大安定集合問題
無向グラフ$G=(V, E)$において、重みの和が最大の安定集合(互いに隣接していない節点の集合)を求めよ。
実行方法
usage
Signature: maximum_stable_set(g, weight='weight')
Docstring:
最大安定集合問題
入力
g: グラフ(node:weight)
weight: 重みの属性文字
出力
最大安定集合の重みの合計と頂点番号リスト
python
# CSVデータ
import pandas as pd, networkx as nx, matplotlib.pyplot as plt
from ortoolpy import graph_from_table, networkx_draw, maximum_stable_set
tbn = pd.read_csv('data/node0.csv')
tbe = pd.read_csv('data/edge0.csv')
g = graph_from_table(tbn, tbe)[0]
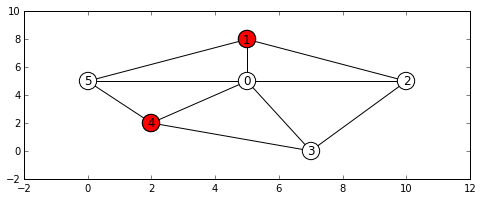
t = maximum_stable_set(g)
pos = networkx_draw(g, node_color='white')
nx.draw_networkx_nodes(g, pos, nodelist=t[1])
plt.show()
print(t)
結果
(5.0, [1, 4])
python
# pandas.DataFrame
from ortoolpy.optimization import MaximumStableSet
MaximumStableSet('data/node0.csv','data/edge0.csv')
| id | x | y | demand | weight | |
|---|---|---|---|---|---|
| 1 | 1 | 5 | 8 | 1 | 3 |
| 4 | 4 | 2 | 2 | 1 | 2 |
python
# 乱数データ
import networkx as nx, matplotlib.pyplot as plt
from ortoolpy import networkx_draw, maximum_stable_set
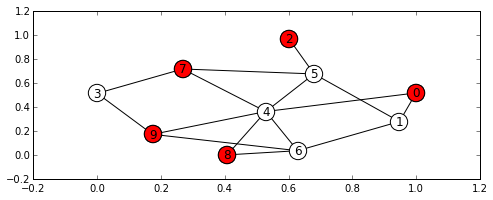
g = nx.random_graphs.fast_gnp_random_graph(10, 0.3, 1)
t = maximum_stable_set(g)
pos = networkx_draw(g, nx.spring_layout(g), node_color='white')
nx.draw_networkx_nodes(g, pos, nodelist=t[1])
plt.show()