最小全域木問題
無向グラフ$G=(V, E)$上の辺$e$の重みを$w(e)$とするとき、全域木$T=(V,E_T)$上の辺の重みの総和$\sum_{e \in E_T}{w(e)}$が最小になる全域木を求めよ。
実行方法
usage
Signature: nx.minimum_spanning_tree(G, weight='weight')
Docstring:
Return a minimum spanning tree or forest of an undirected
weighted graph.
A minimum spanning tree is a subgraph of the graph (a tree) with
the minimum sum of edge weights.
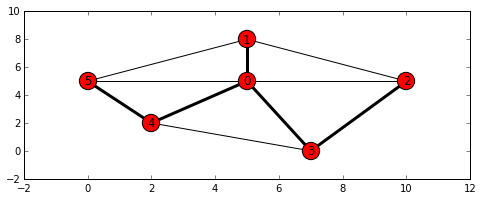
python
# CSVデータ
import pandas as pd, networkx as nx, matplotlib.pyplot as plt
from ortoolpy import graph_from_table, networkx_draw
tbn = pd.read_csv('data/node0.csv')
tbe = pd.read_csv('data/edge0.csv')
g = graph_from_table(tbn, tbe)[0]
t = nx.minimum_spanning_tree(g)
pos = networkx_draw(g)
nx.draw_networkx_edges(t, pos, width=3)
plt.show()
print(t.edges())
結果
[(0, 1), (0, 3), (0, 4), (2, 3), (4, 5)]
python
# pandas.DataFrame
from ortoolpy.optimization import MinimumSpanningTree
MinimumSpanningTree('data/edge0.csv')
| node1 | node2 | capacity | weight | |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 1 |
| 1 | 0 | 3 | 2 | 2 |
| 2 | 0 | 4 | 2 | 2 |
| 3 | 2 | 3 | 2 | 3 |
| 4 | 4 | 5 | 2 | 1 |
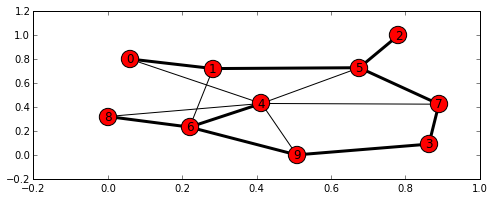
python
# 乱数データ
import math, networkx as nx, matplotlib.pyplot as plt
from ortoolpy import networkx_draw
g = nx.random_graphs.fast_gnp_random_graph(10, 0.3, 1)
pos = nx.spring_layout(g)
for i, j in g.edges():
g.adj[i][j]['weight'] = math.sqrt(sum((pos[i] - pos[j])**2))
t = nx.minimum_spanning_tree(g)
pos = networkx_draw(g, nx.spring_layout(g))
nx.draw_networkx_edges(t, pos, width=3)
plt.show()