FPGA実装する観点でhalf（16bit 浮動小数点）の精度測定

half（16bit 浮動小数点）精度

MATLABで最近half精度と呼ばれる16bitの浮動小数点データ型が使えるようになった。CやHDLコード生成もできるので、マイコンやFPGA実装も可能。（ちなみに、これまで使えた浮動小数点はdouble（64bit）、single（32bit））
16bitの浮動小数点というと精度がそんなに良くないので、どういうところに使うのが適切なのか理解するため、コストと精度を検証してみた。

MATLABの浮動小数点データ型はIEEEフォーマット。
halfだとデータ範囲は-65504～+65504。それ以上または以下はinf扱いになる。

>> half(2^16-17)
ans = 
  half
       65504
>> half(2^16-16)
ans = 
  half
   Inf

浮動小数点フォーマットや固定小数点データ型に関しては他のサイトで取り上げられているので、そちらを参照されたし。
なお、doubleデータ型からsingle, half, 固定小数点への変換時の「丸め」手法は、いずれもバイアスが生じない「最も近い偶数方向」を使用している。

18bit固定小数点データ型との比較

IntelのFPGAは18bitのDSPブロック（積和演算回路）を内蔵しているので、3bitの乗算であろうが16bitであろうが、18bit以下であれば回路の実装コストは同じ。

doubleデータ型の入力信号を単に丸めるだけのモデルで誤差を確認してみた。

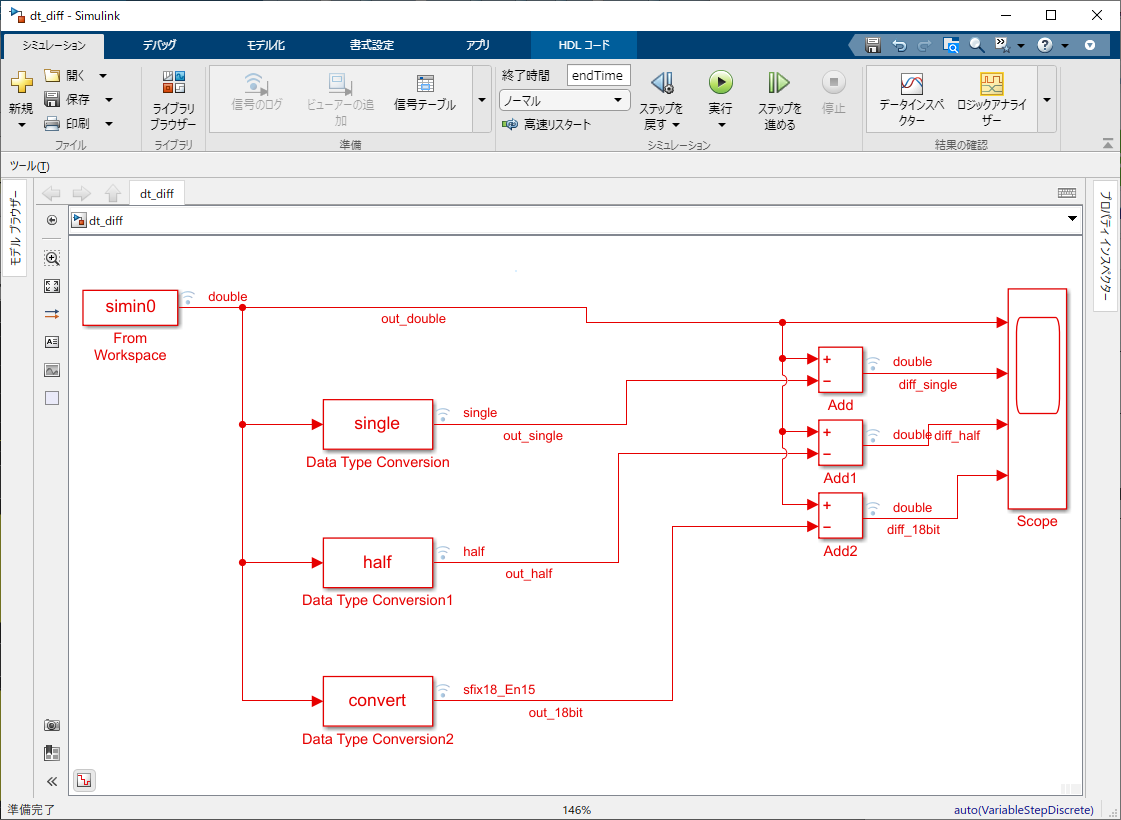
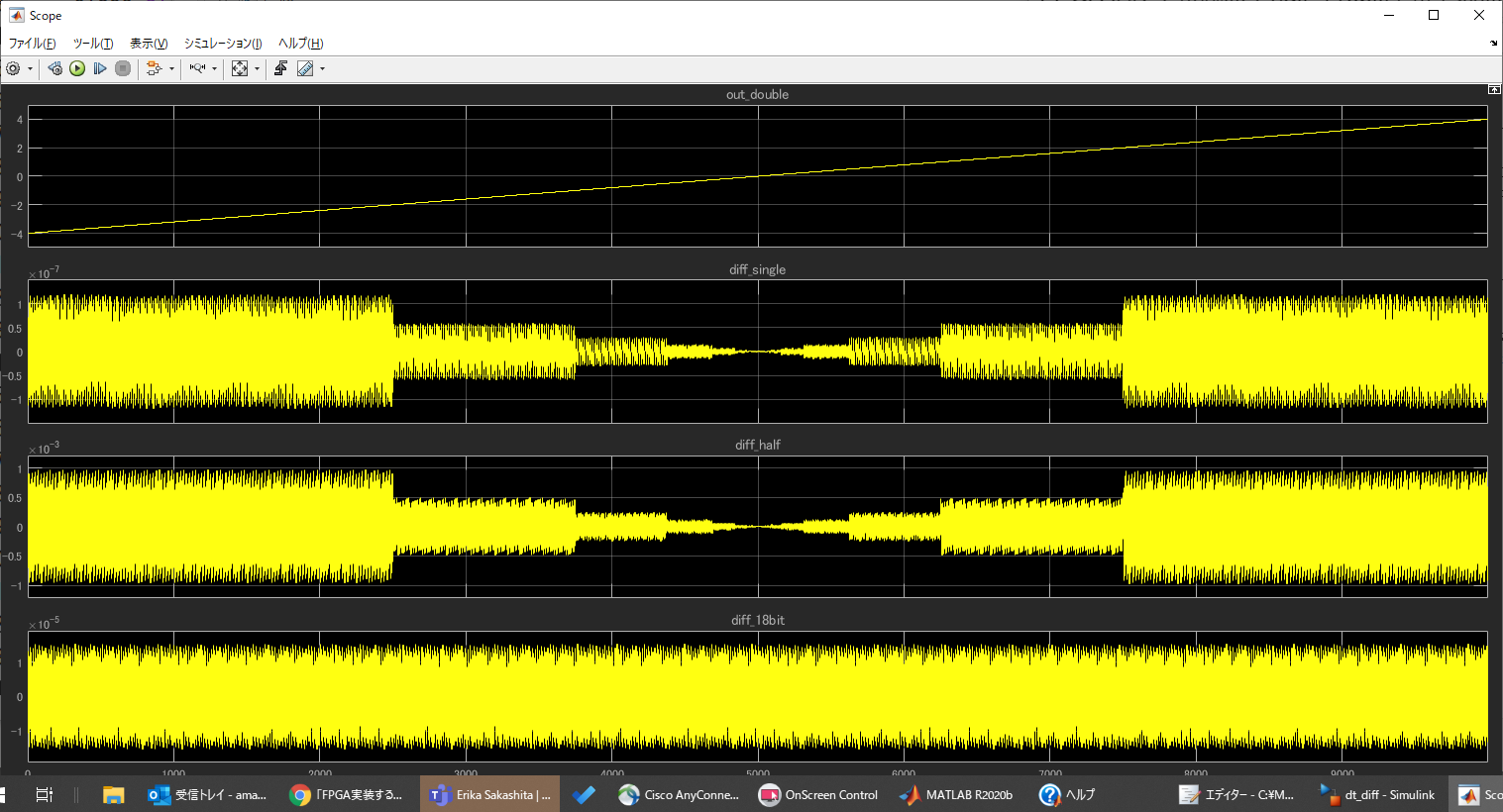
上から順に
1段目は入力信号（doubleで範囲-4～3.999）
2段目はsingle（誤差が $ 10^{-7} $ 程度）
3段目はhalf（誤差が$10^{-3}$程度）
4段目は18bit小数部15bit（誤差は$10^{-5}$程度）
となった。

同じデータ範囲であれば、halfよりも18bit固定小数点のほうが誤差の最大値は小さいが、halfは値が小さくなるにつれ誤差も小さくなっていくのが特徴。

波形は掲載しないが、16bit小数部13bitの固定小数点だと誤差は$5 \times 10^{-5}$程度となった。

データ範囲によって誤差はどう変わるのか？

固定小数点データのビット幅は18bit固定で、スケーリング（小数点位置）、つまりデータ範囲を変えてsingle, half, 固定小数点データ型の誤差についてグラフ化してみた。

こちらはX軸にデータ範囲（$\pm2^2 ～\pm2^{14}$）、Y軸（対数軸）に標準偏差をプロットしたもの。

例えば固定小数点18bitで$\pm2^{12}$のデータ範囲（x軸12）だと、標準偏差は$10^{-2}$で、それと同じ誤差となるhalfのデータ範囲は$\pm2^{7}$程度になる。

こちらはX軸にデータ範囲（$\pm2^2 ～\pm2^{14}$）、Y軸（対数軸）に最大誤差をプロットしたもの。

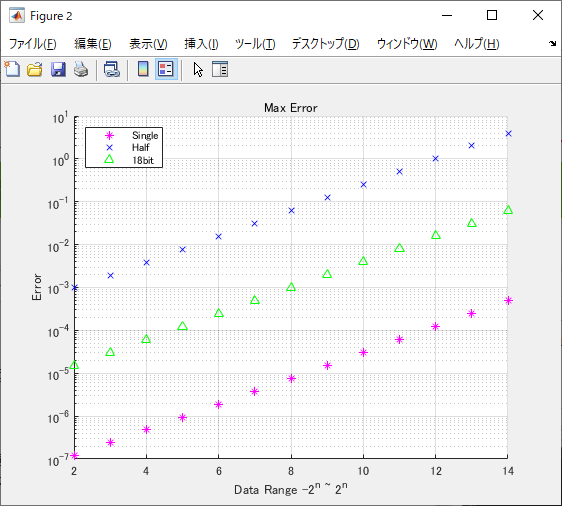
グラフからデータ範囲と誤差は比例関係にあることがわかるので、データ範囲で正規化したそれぞれの標準偏差の相対値は
single：$1.3006 \times 10^{-8}$
half：$1.0655 \times 10^{-4}$
18bit：$2.2025 \times 10^{-6}$

最大誤差の相対値は
single：$2.9775 \times 10^{-8}$
half：$2.4396 \times 10^{-4}$
18bit：$4.5259 \times 10^{-6}$

halfやsingleと同じ誤差になる固定小数点データ型は？

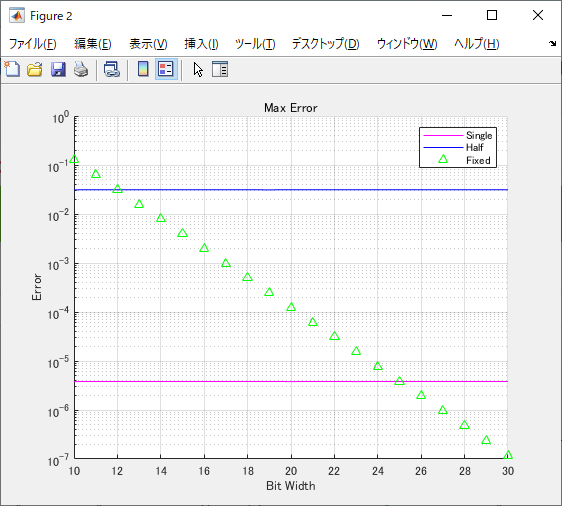
入力信号のデータ範囲はいずれも-128～+127.99。halfやsingleは誤差は一定となる。
固定小数点はビット幅を10～30bitまで変えて、整数部のビット幅は8bit固定にして誤差を測定(8bitのデータ範囲は-128～+127）。つまり小数部のビット幅が2～22bitまで変わる。

浮動小数点はデータ範囲が広いので、固定と浮動を単純に誤差という観点で見るのは無理があるが、データ範囲が決まっていたらという仮定を前提とした誤差。halfと固定小数点12bit、またsingleと25bitがおおよそ同程度の誤差となることがわかる。

参考までに、標準偏差や最大誤差はビット幅が同じであれば、整数部のビット幅を変えても同じ。

まとめ

浮動小数点と固定小数点でデータ範囲と誤差の出方が異なるので、単純に標準偏差や最大偏差という観点だけでは比較が難しいが、なんとか無理やりまとめると

• 浮動小数点はデータの大きさに比例して誤差も大きくなるのに対して、固定小数点はビット幅で誤差が決まる
• halfは12bit固定小数点データ型と、singleは25bit固定小数点データ型と同程度の誤差を持つ（ただし、データがそれぞれ12/25bitの範囲に収まっていてオーバーフローを起こさないという前提）

今後

今回はまず手始めとしてデータ型の観点のみから誤差を比較したが、今後は $exp, sqrt, \div$などの演算の観点での誤差の比較およびFPGA実装コストとULP誤差を測定する予定。

なんかもっと良い誤差の表現方法をご存じであれば教えて欲しい。

MATLABコード

このページで使用したMATLABコードを掲載する。

%%
close all
clear
open_system('dt_diff')

%%
bitWidth = 18;
scallingFactor = 3:(bitWidth-3);
% scallingFactor = bitWidth-3;  % 固定値でシミュレーション
dataPoint = 10000;

%% シミュレーションと誤差計算
for n = 1:numel(scallingFactor)
inDataMin(n) = -2^(bitWidth-1)/2^scallingFactor(n);
inDataMax(n) = (2^(bitWidth-1)-1)/2^scallingFactor(n);
powFactor(n) = nextpow2(inDataMax(n));
inData = linspace(inDataMin(n), inDataMax(n), dataPoint);
% Halfのレンジ +-65504
% 正の最大値：half(2^16-17)。これ以上はInf扱い
% 負の最小値：half(-2^16+17)  同上

t = 0:length(inData)-1;
endTime = t(end);
simin0 = timeseries(inData, t);

%% シミュレーション実行
simDataMin = inDataMin(n);
simDataMax = inDataMax(n);
simBitWidth = bitWidth;

out = sim(gcs)

%% 差分を計算
% Simulinkデータを取得
outDouble = squeeze(out.logsout.getElement('out_double').Values.Data);
outSingle = squeeze(out.logsout.getElement('out_single').Values.Data);
outHalf = squeeze(out.logsout.getElement('out_half').Values.Data);
out18bit = squeeze(out.logsout.getElement('out_18bit').Values.Data);

% 差分
outDiffSingle = outDouble - double(outSingle);
outDiffHalf = outDouble - double(outHalf);
outDiff18bit = outDouble - double(out18bit);

% 標準偏差
stdSingle(n) = std(outDiffSingle)
stdHalf(n) = std(outDiffHalf)
std18bit(n) = std(outDiff18bit)

% 最大誤差
maxSingle(n) = max(abs(outDiffSingle))
maxHalf(n) = max(abs(outDiffHalf))
max18bit(n) = max(abs(outDiff18bit))

end

%% プロット
figure(1), hold on, grid on
set(gca, 'YScale', 'log')
plot(powFactor, stdSingle, 'm*',...
    powFactor, stdHalf, 'bx',...
    powFactor, std18bit, 'g^')
title('Standard Deviation')
xlabel('Data Range -2^n ~ 2^n')
ylabel('Std')
legend('Single', 'Half', '18bit','Location','northwest')


figure(2), hold on, grid on
set(gca, 'YScale', 'log')
plot(powFactor, maxSingle, 'm*',...
    powFactor, maxHalf, 'bx',...
    powFactor, max18bit, 'g^')
title('Max Error')
xlabel('Data Range -2^n ~ 2^n')
ylabel('Error')
legend('Single', 'Half', '18bit','Location','northwest')

%% 標準偏差をデータ範囲で正規化
stdSinglePersentage = stdSingle./(2.^powFactor)
stdHalfPersentage = stdHalf./(2.^powFactor)
std18bitPersentage = std18bit./(2.^powFactor)

meanStdSinglePersentage = mean(stdSinglePersentage)
meanStdHalfPersentage = mean(stdHalfPersentage)
meanStd18bitPersentage = mean(std18bitPersentage)

%% 最大偏差をデータ範囲で正規化
maxSinglePersentage = maxSingle./(2.^powFactor)
maxHalfPersentage = maxHalf./(2.^powFactor)
max18bitPersentage = max18bit./(2.^powFactor)

meanMaxSinglePersentage = mean(maxSinglePersentage)
meanMaxHalfPersentage = mean(maxHalfPersentage)
meanMax18bitPersentage = mean(max18bitPersentage)

%%
close all
clear
open_system('dt_diff')
%%
bitWidth = 10:30;
% scallingFactor = 3:(bitWidth-3);
scallingFactor = bitWidth-8;  % 固定値でシミュレーション
dataPoint = 10000;

%% シミュレーションと誤差計算
for n = 1:numel(bitWidth)
inDataMin(n) = -2.^(bitWidth(n)-1)/2^scallingFactor(n);
inDataMax(n) = (2.^(bitWidth(n)-1)-1)/2^scallingFactor(n);
powFactor(n) = nextpow2(inDataMax(n));
inData = linspace(inDataMin(n), inDataMax(n), dataPoint);

t = 0:length(inData)-1;
endTime = t(end);
simin0 = timeseries(inData, t);

%% シミュレーション実行
simDataMin = inDataMin(n);
simDataMax = inDataMax(n);
simBitWidth = bitWidth(n);

out = sim(gcs)

%% 差分を計算
% Simulinkデータを取得
outDouble = squeeze(out.logsout.getElement('out_double').Values.Data);
outSingle = squeeze(out.logsout.getElement('out_single').Values.Data);
outHalf = squeeze(out.logsout.getElement('out_half').Values.Data);
out18bit = squeeze(out.logsout.getElement('out_18bit').Values.Data);

% 差分
outDiffSingle = outDouble - double(outSingle);
outDiffHalf = outDouble - double(outHalf);
outDiff18bit = outDouble - double(out18bit);

% 標準偏差
stdSingle(n) = std(outDiffSingle)
stdHalf(n) = std(outDiffHalf)
std18bit(n) = std(outDiff18bit)

% 最大誤差
maxSingle(n) = max(abs(outDiffSingle))
maxHalf(n) = max(abs(outDiffHalf))
max18bit(n) = max(abs(outDiff18bit))


end

%% プロット

figure(1), hold on, grid on
set(gca, 'YScale', 'log')
plot(bitWidth, stdSingle, 'm',...
    bitWidth, stdHalf, 'b',...
    bitWidth, std18bit, 'g^')
title('Standard Deviation')
xlabel('Bit Width')
ylabel('Std')
legend('Single', 'Half', 'Fixed','Location','northeast')

figure(2), hold on, grid on
set(gca, 'YScale', 'log')
plot(bitWidth, maxSingle, 'm',...
    bitWidth, maxHalf, 'b',...
    bitWidth, max18bit, 'g^')
title('Max Error')
xlabel('Bit Width')
ylabel('Error')
legend('Single', 'Half', 'Fixed','Location','northeast')