離散フーリエのプログラムを自作した

離散フーリエ変換(DFT)のプログラムを自分で作ってみました。
フーリエ変換は大学3年生の時に授業でやったのですが、昔のことなので忘れてしまいました(sinやcosや積分が出たような気がする程度)。
化学系出身ということもあり、DFTといえば密度汎関数理論の方を思い浮かぶタイプの人ですが、google教授にいろいろ教わりながらやりました。
結論としては、だいぶ簡単でした。

離散フーリエ変換

wikipedia先生曰く
$$ F(t)=\sum_{x=0}^Nf(x)e^{-i \frac{2\pi tx}{N}} $$
ここで、Nは任意の自然数(データ数？)、eはネイピア数、iは虚数単位、πは円周率、tは周波数です。

これをプログラムに落とし込んでいきます。
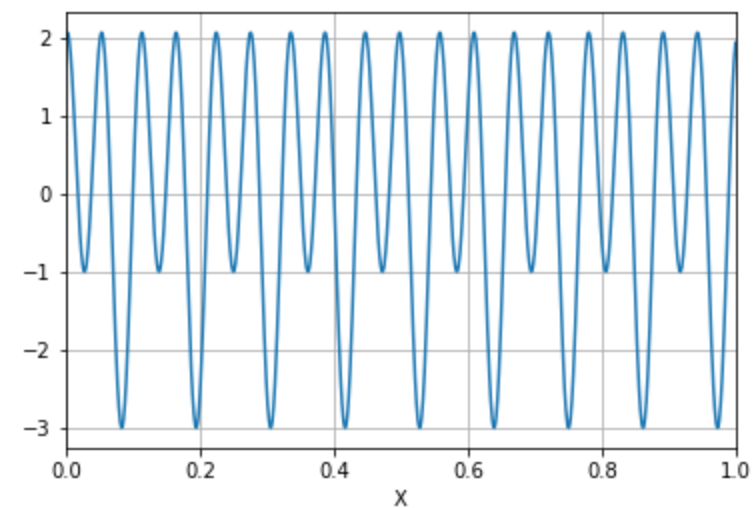
まずは適当に三角関数を足し合わせたものを作ります。
周波数が9で振幅1の正弦波と、周波数18で振幅2の正弦波を重ねました。
$$ y(x) = \sin(9×2\pi x)+2\sin(18×2\pi x)$$

グラフ描画はpandasのplotを使いました。

dft.py

%matplotlib inline
import numpy as np
import pandas as pd
import math
import cmath

sintest = np.zeros(1000)
x = np.zeros(1000)
for i in range(0,1000):
    sintest[i] = math.sin(i*(9*2*cmath.pi)/1000)+2*math.cos(i*(18*2*cmath.pi)/1000)
    x[i] = i/1000

df = pd.DataFrame([x,sintest]).T
df.columns = ["X","Y"]
df.plot(x="X",y="Y",grid = True,legend = False)

↓作った関数

これをフーリエ変換します。wikipedia先生の式をそのままコードにします。

dft.py

result = np.zeros(sintest.shape[0])
N = sintest.shape[0]
for i in range(0,N):
    temp = 0j
    for k in range(0,N):
        temp = temp + sintest[k]*cmath.exp(-1j*2*pi*i*k/N) 
    result[i] = abs(temp)
result_pd = pd.DataFrame(result)
result_pd.plot(logy=False,grid = True,xlim = [0,100])

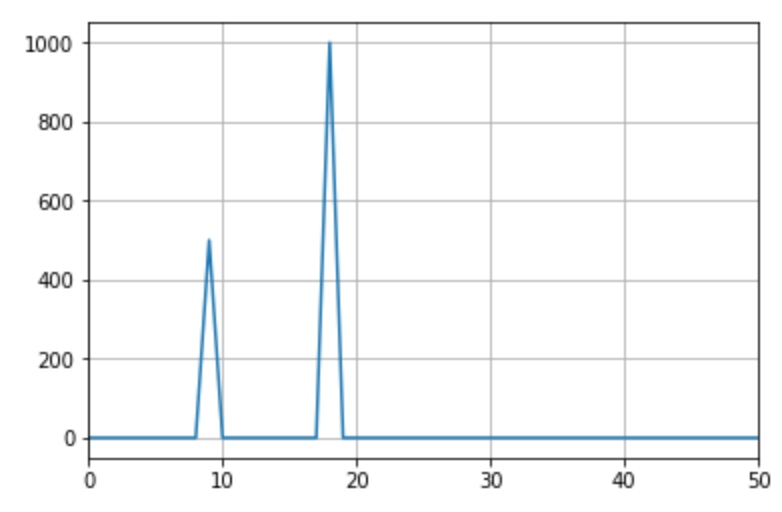
ちゃんと9と18にピークが立ちました。ピーク比も振幅比と一致しています。

感想

たったの数行で離散フーリエ変換ができるとは思わなかったです。もう少し難しいと勝手に思っていました。
次は高速フーリエ変換をしたいです。

おまけ(為替データの離散フーリエ変換)

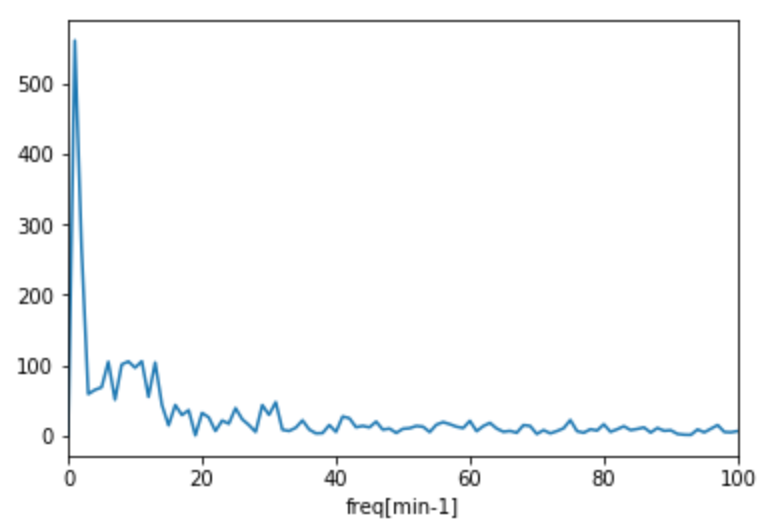
為替データをフーリエ変換することで「いつ外貨を売買すれば儲かるか」を調べるため、2020年1月17日4時10頃から20時50分頃までのUSD/JPYの為替データをフーリエ変換してみました。
周波数が1min^-1でピークがあり、それ以外の成分は小さいです。
1分間の変動なんてほとんどが0.5銭未満なので、スプレットを支払う機械にしかなりません。

(そもそも1分のサンプリング周期なのに周波数1min^-1の成分ってどんな意味があるんだ・・・)