注意!
この記事を書いた人間は技術的にガバガバです。書いてあることの正しさは保証できません。間違い等の指摘等はありがたく受け付けますのでどうぞ宜しくお願いします。
0.まえがき
C#で信号処理をやろうとするのが間違いな気もするが、兎にも角にも「音声信号をFFTかけてスペクトルにしたい、なるべく早くかつ無駄なくやりたい」という事情があったので、「入力は実数、逆変換はする予定が無いのでやらない」という条件のもとネイティブCの大浦FFTライブラリをC#に移植した。「大浦FFT」とは、京大の数理解析研究所で助教をやってらっしゃる、大浦先生という方が作ったライブラリだ。
大浦FFT公式ページ
www.kurims.kyoto-u.ac.jp/~ooura/fftman/index.html
クッソ早くてネイティブCだからCコンパイラが走る環境なら移植も楽勝、公式サイトの解説も細かく書かれており、しかも商用非商用問わず好きに使っていいし改造しても良い。こんな素晴らしい代物を移植しようとする人は当然いらっしゃって、例えばC++/javaであればこちらの方がやっておられる。大いに参考にさせてもらった。というか途中までやってることは同じだ。
で、この大浦FFTの内訳は、まぁパッケージのページを見ればわかるんだが、
・基数4,2版
・基数8,4,2版
・スプリットラディックス版(以下SR版)
の3つがある。簡易版については実質下位互換らしいので省略する。
この内、SR版は解説にもある通り、
Split-Radix FFT は,いかなる基数の Cooley-Tukey FFT よりも 浮動小数点演算回数が少ないアルゴリズムとして知られています
との事だ。ちなみに具体的には、「加、減、乗算の総回数が他の方法より最小」らしい。一般に除算以外は概ね似たような速度で計算できるらしい1ので、もう全部あいつ一人でいいんじゃないかな。
目標
SR版FFTは、「複素フーリエ変換」「実数フーリエ変換」「離散コサイン変換」「聞いたこともねぇようなよくわからん変換3つ」に機能が分かれていて、更にそれぞれ変換/逆変換とあるので実質12の関数を公開している。とはいえ、「音声のスペクトルみたい!」というシチュエーションであれば、__必要なのは「実数フーリエ順方向変換」ただ一つ__だ。今回はこれに絞って移植した…が、手順は同じなのでやろうと思えば誰でも出来る筈だ。
方針としては、まずネイティブCのコードから使う予定のない機能を削り、オブジェクト指向っぽくカプセル化してC++コードに直す。ここまでは先程の「C++とJavaに移植した」の人と同じだ。次にこれを静的ライブラリとして吐き、それをC++/CLIでラップしてマネージコードと橋渡しをする。これでC#からでも触れるDllが吐けるわけだ。微妙に無駄が多い気もするが、C++向けに纏めたライブラリも手に入るので損はしないだろう。
1.作業内容
1.1.ネイティブCからC++へ
まず、大本のfftsg.cからいらん部分を削る。今回は「rdft」関数と、そこから呼ばれている関数を除いて全て消す。関数内で呼ばれているプロトタイプ宣言を片っ端から消したらクラスで包んでやり、折角オブジェクト指向なので一手間加えてそれっぽくする。
OouraRdft::OouraRdft(int length)
{
work = new int[2 + (int)(sqrt(0.5 * length) + 1)];
table = new double[length * 5 / 4];
size = length;
work[0] = 0;
}
コンストラクタ。元のソースコードにおいて、workはip、tableはwにあたる。workもといipはビット逆転(反転ではなく逆転、0001を1000にするような操作)を効率良く行うためのワークメモリ。tableはsinとcosを手早く引くためのテーブルだそうだ。大本は「ip[0]が0だったら初期化処理を行う」という中々クセのある挙動をするので、コンストラクタで自動的にそこら辺を覆う。こうすれば使う側からすると配列の長さだけ考えれば良い。また、本来は呼び出すFFTのタイプによって異なるサイズのワークメモリが要るのだが、今回はRDFTしか使わないので決め打ちだ。ワークメモリをクラスのフィールドにすることで、rdft関数はこのように纏まる。
void OouraRdft::rdft(double *a)
{
int nw, nc;
double xi;
nw = work[0];
if (size > (nw << 2)) {
nw = size >> 2;
makewt(nw, work, table);
}
nc = work[1];
if (size > (nc << 2)) {
nc = size >> 2;
makect(nc, work, table + nw);
}
//本格的フーリエ変換
if (size > 4) {
cftfsub(size, a, work, nw, table);
rftfsub(size, a, nc, table + nw);
}
else if (size == 4) {
cftfsub(size, a, work, nw, table);
}
xi = a[0] - a[1];
a[0] += a[1];
a[1] = xi;
}
データ列を受け取り、データ列を返す、シンプルな関数に落ち着いた。
更に、RDFTが返すデータは、__「a[偶数番地]に実数部、a[基数番地]に虚数部」__という形式なのだが、実際にスペクトルを出す場合は実数部と虚数部の加算ベクトルの絶対値を見るのが普通なので、ついでにそれも纏めて書いてしまう。
void OouraRdft::rdftPower(double * a, double * result, bool isDb)
{
rdft(a);
for (int i = 0; i < size / 2; i++) {
result[i] = sqrt(a[2 * i] * a[2 * i] + a[2 * i + 1] * a[2 * i + 1]);
if (isDb) {
result[i] = 20.0*log10(result[i]);
}
}
}
ここまでで、こんな使い方が出来るようになった。
# include "OouraRdft.h"
# include <iostream>
# include <Windows.h>
# include <cstdlib>
# include <cmath>
using namespace std;
//サンプルとして1000ヘルツのサイン波をぶっこむ
void setdata(double *a, int num) {
auto om = atan(1.0)*8.0 / 44100;
for (int i = 0; i < num; i++) {
a[i] = sin(1000 * om*i); //1000hz
}
}
int main() {
OouraRdft dft(8192); //オブジェクトつくる
LARGE_INTEGER qf, qc, qo; //時間計測用の変数
double a[8192];
QueryPerformanceFrequency(&qf);
setdata(a, 8192);
//1000回FFTして計測を10セット
for (int j = 0; j < 10; j++) {
QueryPerformanceCounter(&qc);
for (int i = 0; i < 1000; i++) {
dft.rdft(a);
}
QueryPerformanceCounter(&qo);
cout << j << ":" << (double)(qo.QuadPart - qc.QuadPart)*1000.0 / qf.QuadPart << "[ms]" << endl;
}
system("pause");
}
コレの結果はこう。
0:44.5374[ms]
1:42.4955[ms]
2:43.7591[ms]
3:42.5391[ms]
4:42.5643[ms]
5:42.8539[ms]
6:42.6512[ms]
7:43.3533[ms]
8:42.734[ms]
9:42.9007[ms]
C++版のソースはこちら。
http://www.mediafire.com/file/b88lq212tvd3m6d/cpp_wrapped.zip
これをスタティックライブラリとしてビルドし、次にマネージコードに直す。
単にソースの中に組み込んで使う場合は、そのままソースをプロジェクトに追加すれば良い。
1.2.C++からマネージドDLLへ
C++のスタティックライブラリをC++/CLIにラップするのは半ば機械的に可能だ。
この記事を参考にさせていただく。
http://d.hatena.ne.jp/licheng/20160223/p1
# pragma once
# include "dft.h"
using namespace System;
namespace Oourardft {
public ref class OouraRDFT
{
public:
OouraRDFT(int size);
~OouraRDFT();
!OouraRDFT();
void rdft(cli::array<double>^ a);
void rdftPower(cli::array<double>^ a, cli::array<double>^ p, bool isDb);
private:
OouraRdft* hontai;
};
}
まぁ概ねこんな感じで。DLLが無事吐けたら、C#でテストする。
マネージドDLLなので、C#で使うのは簡単だ。参照設定にDLLを読ませ、using namespaceすればクラスが覗ける。
using System;
using System.IO;
using Oourardft;
using static System.Math;
using System.Diagnostics;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
test();
}
//テストデータを作る 1000ヘルツのサイン波
static double[] testdata(int num)
{
var sr = 2 * PI / 44100.0; //44100ヘルツとした時の角速度
var ret = new double[num];
for (int i = 0; i < num; i++)
{
ret[i] = Sin(1000.0 * sr * i); //1000ヘルツ
}
return ret;
}
static void test()
{
const int num = 8192;
var data = testdata(num);
var dft = new OouraRDFT(num);
Stopwatch sw = new Stopwatch();
for (int j = 0; j < 10; j++)
{
sw.Start();
for (int i = 0; i < 1000; i++)
{
dft.rdft(data);
}
sw.Stop();
Console.WriteLine($"{j}:{sw.ElapsedTicks * 1000.0 / (double)Stopwatch.Frequency}[ms]");
sw.Reset();
}
Console.ReadKey();
}
}
}
0:45.2585620491281[ms]
1:44.0089866443766[ms]
2:50.4812664626659[ms]
3:43.6049445853829[ms]
4:44.3466148384958[ms]
5:43.8135484869488[ms]
6:43.4996186322781[ms]
7:46.3554148218777[ms]
8:43.0104380945248[ms]
9:50.4657601417921[ms]
結構適当にベンチマーク2してしまったので余り当てにならないのだが、概ね8,9割程度の速度が出ているようだ。まぁ上場じゃあないか。たぶん…。
けつろん
というわけで、出来上がったライブラリはこちら。
http://www.mediafire.com/file/96yuvfcydf70sp8/OouraRDFTlib.zip
中身は32ビット版と64ビット版に分かれてるので環境に合わせて入れて欲しい。
実用的な使い方を書くとこんな感じだ。
using System;
using System.IO;
using Oourardft;
using static System.Math;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
const int SIZE = 8192;
var dft = new OouraRDFT(SIZE); //サイズを決める 2^nじゃないと例外
var data = testdata(SIZE);
var db = new double[SIZE / 2]; //周波数成分はサンプリング定理からサンプル数の半分までしか出ない
//fftを実行、デシベルに直してスペクトルを得る
dft.rdftPower(data, db, true); //末尾のフラグはデシベルに直すフラグ trueの場合20*log10(ベクトル長)を計算
//テキストに吐いてみる
var sw = new StreamWriter("result.txt");
for(int i=0; i < db.Length; i++)
{
sw.WriteLine($"{i*44100.0/SIZE} {db[i]}"); //サンプリングレートをフーリエ変換に突っ込んだサンプル数で割ったのが周波数分解能
}
sw.Close();
Console.WriteLine("end");
Console.ReadKey();
}
//テストデータつくる 1khのサイン波
static double[] testdata(int num)
{
var sr = 2 * PI / 44100.0; //44100ヘルツとした時の角速度
var ret = new double[num];
for (int i = 0; i < num; i++)
{
ret[i] = Sin(1000.0 * sr * i); //1000ヘルツ
}
return ret;
}
}
}
さて、このテストプログラムで吐いたテキストをグラフ化して見てみよう。
グラフはRinearnGraph2Dを使った。
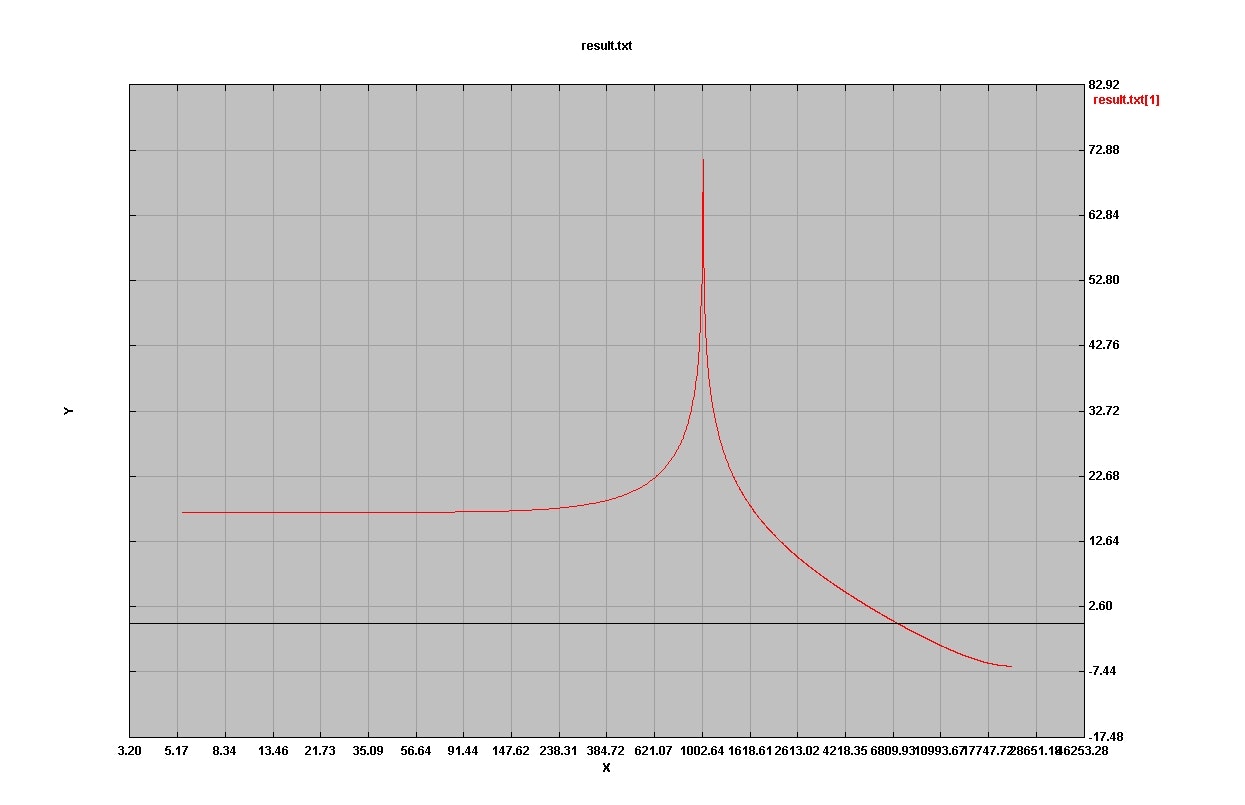
まぁ、期待通りの結果が出ている。1000ヘルツにピークを持つパワーがどばっと出ているわけだ。妙に山の裾野が広がっているのは、窓関数をかけていないからであり、これも予想通りの結果と言える。
おわり
というわけでとりあえず実用重視のオーディオ向けFFTが出来た。ロクにデバッグしてないのであまり虐めないで欲しいが、もしバグ見つけたとかもっと良い実装あるとかであれば、折角大浦先生も勝手に弄ってくれてOKと言ってるのだし是非やってみて欲しい。ちなみにここまで書いてみて、「デシベルになおして吐くやつ、メソッド内で配列作ってそれ返したほうがよくね?」とか思ったけど、もう眠いから知らん。
-
プログラムによる数値演算のベンチマークより。なまじ情報が古い気もするが、そう大きくは違わんだろう…という事で… ↩
-
全て最適化レベルは最大(Ox)、Releaseビルドでx64向け。Windows 8.1、Core-i5 4690K、Visual Studio 2015 ↩