NetworkXで作成できるグラフのリストです。
前情報
NetworkXの公式ドキュメントを和訳したものです。バージョンは2.4です。全ては網羅できていません。訳語が間違っている場合はお知らせください。
動作確認はJupyter notebook上で行っています。コードを実行するにはあらかじめnetworkxとmatplotlib.pyplotをインポートしておいてください。
import networkx as nx
import matplotlib.pyplot as plt
Classic(古典的グラフ)
balanced_tree(平衡木)
balanced_tree(r, h, create_using=None)
高さがhである完全平衡r分木を返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| r | int | 木の枝分かれ数。各ノードはr個の子ノードを持ちます。 |
| h | int | 木の高さ |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
コード
#balanced_tree
G=nx.balanced_tree(3,2)
plt.cla()
nx.draw_networkx(G)
plt.show()
barbell_graph(バーベルグラフ)
barbell_graph(m1, m2, create_using=None)
バーベルグラフ(m1個のノードで構成された2つの完全グラフがm2個のノードからなる1本の道によってつながれたグラフ)を返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| m1 | int | 左右の完全グラフ(bell)の個数。m1>1 |
| m2 | int | 左右の完全グラフをつなぐ経路のノード数。m2>=0 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
ノードのナンバリング方法
左の完全グラフ:0,1,...,m1-1
経路:m1,m1+1,...,m1+m2-1
右の完全グラフ:m1+m2,m1+m2+1,...,2*m1+m2-1
例1
コード
#barbell_graph
G=nx.barbell_graph(5,2)
plt.cla()
nx.draw_networkx(G)
plt.show()
例2(m2=0のとき)
コード
G=nx.barbell_graph(5,0)
plt.cla()
nx.draw_networkx(G)
plt.show()
binomial_tree(二項木)
binomial_tree(n)
次数がnである二項木を返します。ノード数は$2^n$個、エッジ数は$2^n-1$個です。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | 木の次数 |
例
コード
G=nx.binomial_tree(3)
plt.cla()
nx.draw_networkx(G)
plt.show()
complete_graph(完全グラフ)
complete_graph(n, create_using=None)
あるノードが他のすべてのノードと連結しているグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int または iterable container of nodes | nが整数型のとき、ノードはrange(n)から作成されます。nがノードのイテラブルコンテナであるとき、それらノードによるグラフが作成されます |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例1(nが整数型のとき)
コード
G=nx.complete_graph(6)
plt.cla()
nx.draw_networkx(G)
plt.show()
例2(nがノードのコンテナであるとき)
コード
G=nx.complete_graph(range(12,18))
plt.cla()
nx.draw_networkx(G)
plt.show()
complete_multipartite_graph(完全多部グラフ)
complete_multipartite_graph(*subset_sizes)
| パラメータ | 型 | 説明 |
|---|---|---|
| subset_sizes | taple of integers または tuple of node iterables | nが整数型のとき、多部グラフの各サブセットはn個の頂点をもちます。nがイテラブルであるときは、それらノードによるグラフが作成されます |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
それぞれ2,3,3個のノードをもつ3つのサブセットからなる完全多部グラフを作成します。
コード
G=nx.complete_multipartite_graph(2,3,3)
plt.cla()
nx.draw_networkx(G)
plt.show()
circular_ladder_graph(環状ラダーグラフ)
circular_ladder_graph(n, create_using=None)
長さnの環状ラダーグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | 1周の長さ |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
コード
G=nx.circular_ladder_graph(10)
plt.cla()
nx.draw_networkx(G)
plt.show()
circulant_graph(循環グラフ)
circulant_graph(n, offsets, create_using=None)
n個のノードからなる、循環グラフを返します。あるノードが他のどのノードとつながるかはoffsetsで指定されます。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | ノードの個数 |
| offsets | lists of integers | ノードオフセットのリスト |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
コード
G=nx.circulant_graph(10,[1,2])
plt.cla()
nx.draw_networkx(G)
plt.show()
offsets=[1,2]であることから、頂点iは頂点i+1,i+2とそれぞれつながっています。頂点0は頂点1,2に、頂点1は頂点2,3に,...,頂点9は頂点0,1につながっています。
cycle_graph(閉路グラフ)
cycle_graph(n, create_using=None)
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int またはiterble container of nodes | nが整数型のとき、ノードはrange(n)から作成されます。nがノードのイテラブルコンテナであるとき、それらノードによるグラフが作成されます |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
コード
G=nx.cycle_graph(10)
plt.cla()
nx.draw_networkx(G)
plt.show()
dorogovtsev_goltsev_mendes_graph(Dorogovstev-Goltsev-Mendesグラフ)
dorogovtsev_goltsev_mendes_graph(n, create_using=None)
Dorogovstev-Goltsev-Mendesアルゴリズムによって作成されたグラフを返します。
元論文
https://arxiv.org/abs/cond-mat/0112143
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | 世代数 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
コード
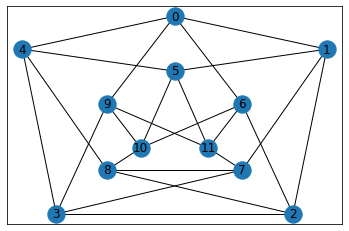
G=nx.dorogovtsev_goltsev_mendes_graph(3)
plt.cla()
nx.draw_networkx(G)
plt.show()
empty_graph(ノードをもつ空グラフ)
empty_graph(n=0, create_using=None, default=<class 'networkx.classes.graph.Graph'>)
エッジを持たないn個のノードからなるグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | ノード数 |
| create_using | Graph Instance, Constructor or None | 作成したいグラフの型。Noneが指定されたときはdefaultコンストラクタを使います。 |
| default | Graph constructor (optional, default = nx.Graph) |
create_using=Noneのときに使用されるコンストラクタ。 |
例
コード
G=nx.empty_graph(10)
plt.cla()
nx.draw_networkx(G,pos)
plt.show()
create_usingの使い方
変数 create_using は Graph コンストラクタまたは "graph" ライクなオブジェクトでなければなりません。
create_usingの主な用途は3つあります。
- 空グラフの性質を指定する。
- 既存のグラフを空グラフにする
- 自作のグラフ作成関数を作るとき、create_usingに好きなグラフコンストラクタを渡せるようにする。
1の例
空の有向グラフ(DiGraph)を作成します。
n = 10
G = nx.empty_graph(n, create_using=nx.DiGraph)
2の例
完全グラフG1からエッジを取り除いた空グラフG2を作成します。
n=5
G1=nx.complete_graph(n)
G1.number_of_edges() #10
G2=nx.empty_graph(n,create_using=G1)
G2.number_of_edges() #0
##3の例
自作のグラフ作成関数mygraphについて、create_usingの指定がないときはデフォルトコンストラクタnx.MultiGraphを使い、そうでないときは指定されたコンストラクタを使うように設定します。
def mygraph(n, create_using=None):
G = nx.empty_graph(n, create_using, default=nx.MultiGraph)
G.add_edges_from([(0, 1), (0, 1)])
return G
G = mygraph(3)
G.is_multigraph() #True
G = mygraph(3, nx.Graph)
G.is_multigraph() #False
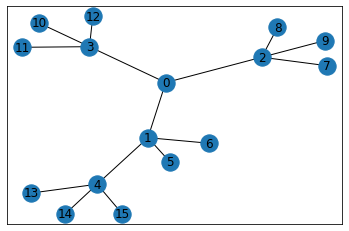
full_rary_tree(全r分木)
full_rary_tree(r, n, create_using=None)
n個のノードから構成された全r分木を作成します。すべてのノードが葉であるかr個の子ノードを持っています。
| パラメータ | 型 | 説明 |
|---|---|---|
| r | int | 木の枝分かれ数 |
| n | int | ノード数 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
コード
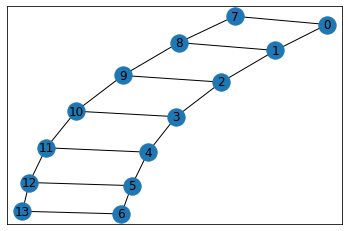
ladder_graph(ラダーグラフ)
ladder_graph(n, create_using=None)
ラダーグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | ラダーの長さ |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
| 例 |
コード
G=nx.ladder_graph(7)
plt.cla()
nx.draw_networkx(G)
plt.show()
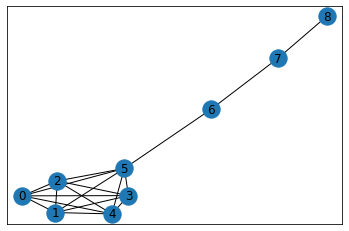
lollipop_graph(ロリポップグラフ)
lollipop_graph(m, n, create_using=None)
ロリポップグラフ(m個のノードからなる完全グラフとそれにつながるn個のノードからなる経路)を返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| m | int or iterable container of nodes (default = 0) | 完全グラフを構成するノード数 |
| n | int or iterable container of nodes (default = 0)) | 経路を構成するノード数 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
コード
G=nx.lollipop_graph(6,3)
plt.cla()
nx.draw_networkx(G)
plt.show()
null_graph(空グラフ)
null_graph(create_using=None)
ノードもエッジも持たないグラフを返します。
create_usingの使い方についてはempty_graphを参照してください。
| パラメータ | 型 | 説明 |
|---|---|---|
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例
コード
G=nx.null_graph()
plt.cla()
nx.draw_networkx(G)
plt.show()
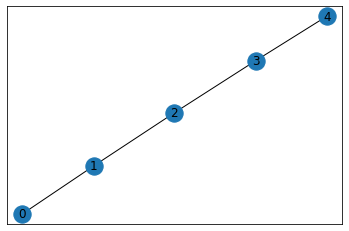
path_graph(道グラフ)
path_graph(n, create_using=None)
n個のノードからなる、同じノードを2度通らないグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int or iterable | ノードの個数 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
コード
G=nx.path_graph(5)
plt.cla()
nx.draw_networkx(G)
plt.show()
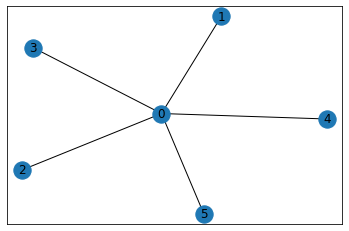
star_graph(星グラフ)
star_graph(n, create_using=None)
1つの中心ノードに対しn個の外周ノードが連結されたグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int or iterable | 外周ノードの個数 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
コード
G=nx.star_graph(5)
plt.cla()
nx.draw_networkx(G)
plt.show()
trivial_graph(トリビアルグラフ)
trivial_graph(create_using=None)
1個のノードのみからなる最も単純なグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
コード
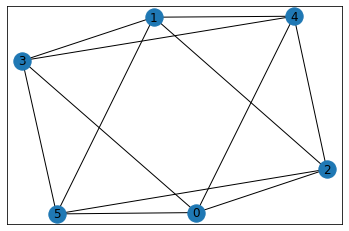
turan_graph(トゥラーングラフ)
turan_graph(n, r)
n個のノードをr個の非連結部分に分けた完全多部グラフを返します。
エッジの数はn**2*(r-1)/(2*r)の端数を切り捨てた数になります。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | ノードの個数。 |
| r | int | 非連結部分の個数。1<=r<=nである必要があります。 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
コード
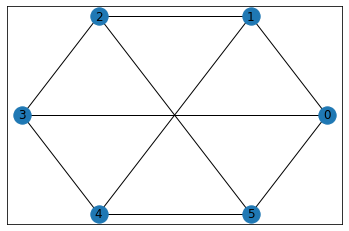
G=nx.turan_graph(6,3)
plt.cla()
nx.draw_networkx(G)
plt.show()
ノードは(0,1),(2,3),(4,5)の3部分に分かれています。同じ部分に属しているノードは連結していません。
例で挙げたグラフは「3組のカップルがカクテルパーティーへ出かけた。会場では、全員が自身とその配偶者を除くすべての参加者とそれぞれ握手をする。そのときの関係性を参加者をノード、握手をエッジとして表現するとどのようなグラフになるか?」という問いに対する解答となっています。そのため「カクテルパーティーグラフ」と呼ばれます。
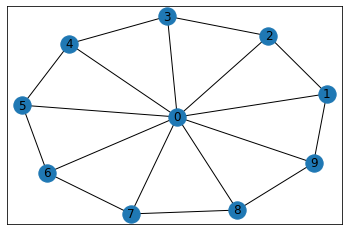
wheel_graph(ホイールグラフ)
wheel_graph(n, create_using=None)
1つのハブノードに対し、n-1個の外周ノードが連結されたグラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int or iterable | ノードの個数。 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
Example
コード
G=nx.wheel_graph(10)
plt.cla()
nx.draw_networkx(G)
plt.show()
Expander graph(拡張グラフ)
強連結成分をもつ疎グラフです。
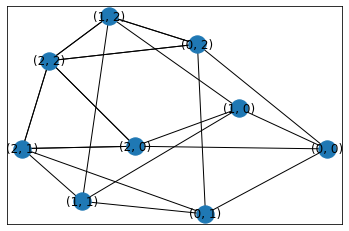
margulis_gabber_galil_graph(Margulis-Gabber-Galilグラフ)
margulis_gabber_galil_graph(n, create_using=None)
Margulis-Gabber-Galilグラフを返します。無向多重グラフであり、ノードの次数は8です。このグラフの隣接行列の2番目に大きな固有値は$5\sqrt{2}$です。
グラフが有向または多重グラフでないときはエラーが返されます。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int or iterable | ノードの個数を定義します。ノードの個数は$n^2$です。 |
| create_using | NetworkX graph constructor, optional (default MultiGraph) | 作成したいグラフの型 |
コード
G=nx.margulis_gabber_galil_graph(3)
pos=nx.circular_layout(G)
plt.cla()
nx.draw_networkx(G)
plt.show()
chordal_cycle_graph(弦を持つ閉路グラフ)
chordal_cycle_graph(p, create_using=None)
弦(chord, 閉路の一部ではないが閉路グラフ上の2つのノード間を連結するエッジ)をもつ閉路グラフを返します。ノードxはx*y=1(mod p)を満たすノードyに対し弦を持ちます。
グラフが有向または多重グラフでないときはエラーが返されます。
| パラメータ | 型 | 説明 |
|---|---|---|
| p | prime number | ノードの個数を定義します。素数である必要があります。 |
| create_using | NetworkX graph constructor, optional (default MultiGraph) | 作成したいグラフの型 |
コード
G=nx.chordal_cycle_graph(7)
pos=nx.circular_layout(G)
plt.cla()
nx.draw_networkx(G,pos)
plt.show()
Lattice(格子)
grid_2d_graph(2次元格子グラフ)
grid_2d_graph(m, n, periodic=False, create_using=None)
2次元の格子グラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| m,n | int or iterable container of nodes | 整数型のとき、ノードはrange(n)から作成されます。ノードのコンテナであるときは、それらの要素がノード座標となります。 |
| periodic | bool(default:False) | Trueならば格子の端にあるノードは反対側のノードとつながり、トーラスになります。 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
例1
コード
#grid_2d_graph
G=nx.grid_2d_graph(4,6)
plt.cla()
nx.draw_networkx(G)
plt.show()
例2
コード
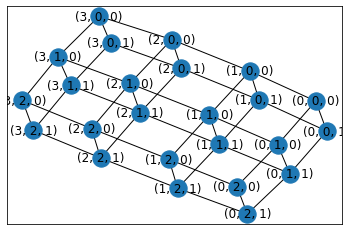
grid_graph(格子グラフ)
grid_graph(dim, periodic=False)
n次元の格子グラフを返します。nはdimの長さです。
| パラメータ | 型 | 説明 |
|---|---|---|
| dim | list or tuple of numbers or iterables of nodes | dimには各次元について、その次元のサイズを表す数値を表すリストやタプルが入ります。または、その次元のノードのイテラブルが入ります。grid_graph の次元イコール dim の長さです. |
| periodic | bool(default:False) | Trueならば格子の端にあるノードは反対側のノードとつながり、トーラスになります。 |
例1
コード
dim=[2,3,4]
G=nx.grid_graph(dim)
plt.cla()
nx.draw_networkx(G)
plt.show()
G = nx.grid_graph(dim=[range(7, 9), range(3, 6)])
plt.cla()
nx.draw_networkx(G)
plt.show()
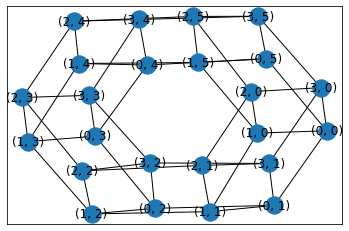
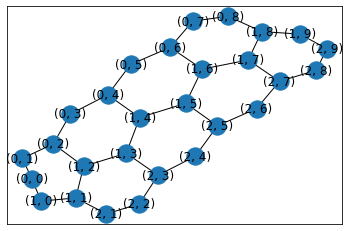
hexagonal_lattice_graph(六角形格子グラフ)
hexagonal_lattice_graph(m, n, periodic=False, with_positions=True, create_using=None)
六角形格子グラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| m | int | 六角形の行数 |
| n | int | 六角形の列数 |
| periodic | bool(default:False) | Trueならば格子の端にあるノードは反対側のノードとつながります。この機能を使いたい場合、nは奇数かつn>1かつm>1である必要があります。 |
| with_positions | bool(default:True) |
posに各ノードの座標を保管するかどうか |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
G=nx.hexagonal_lattice_graph(4,2)
plt.cla()
nx.draw_networkx(G)
plt.show()
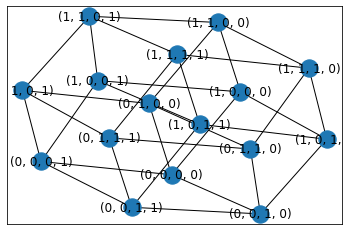
hypercube_graph(超立方体グラフ)
hypercube_graph(n)
n次元の超立方体グラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| n | int | 超立方体の次元の数。ノードの数は2のn乗個です。 |
G=nx.hypercube_graph(4)
plt.cla()
nx.draw_networkx(G)
plt.show()
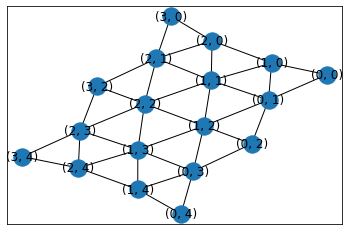
triangular_lattice_graph(三角格子グラフ)
triangular_lattice_graph(m, n, periodic=False, with_positions=True, create_using=None)
m行n列の三角格子グラフを返します。
| パラメータ | 型 | 説明 |
|---|---|---|
| m | int | 行数 |
| n | int | 列数 |
| periodic | bool(default:False) | Trueならば格子の端にあるノードは反対側のノードとつながります。m>=3かつn>=5である必要があります。mまたはnが奇数のときはずれてつながります。 |
| with_positions | bool(default:True) | グラフノード属性posに各ノードの座標を保管するかどうか |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
G=nx.triangular_lattice_graph(4,5)
plt.cla()
nx.draw_networkx(G)
plt.show()
Small
make_small_graph(スモールグラフをつくる)
make_small_graph(graph_description, create_using=None)
graph_descriptionの情報をもとに小さなグラフを作ります。
graph_descriptionは[Itype,name,n,xlist]という形式のリストです。ここで、Itypeは"adjacencylist"または"edgelist"のどちらかです。nameはグラフの名前、nはノードの個数です。
Itype="adjacencylist"のときは、xlistには隣接リストを指定します。
Itype="edgelist"のときは、xlistにはエッジリストを指定します。
| パラメータ | 型 | 説明 |
|---|---|---|
| graph_description | [Itype,name,n,xlist] | Itypeは"adjacencylist"または"edgelist"のどちらかです。nameはグラフの名前、nはノードの個数です。 |
| create_using | NetworkX graph constructor, optional (default=nx.Graph) | 作成したいグラフの型 |
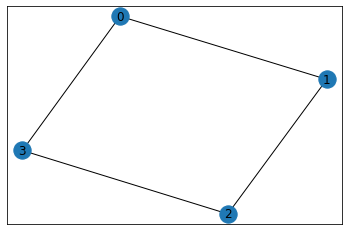
例1
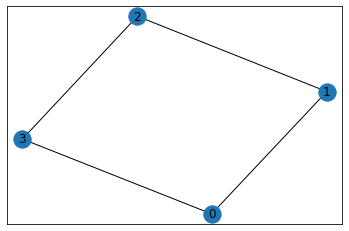
G=nx.make_small_graph(["adjacencylist","C_4",4,[[2,4],[1,3],[2,4],[1,3]]])
plt.cla()
nx.draw_networkx(G)
plt.show()
例2
G=nx.make_small_graph(["edgelist","C_4",4,[[1,2],[3,4],[2,3],[4,1]]])
plt.cla()
nx.draw_networkx(G)
plt.show()
LCF_graph(LCFグラフ)
LCF_graph(n, shift_list, repeats, create_using=None)
LCF(Lederberg-Coxeter-Fruchte)表記法を用いてグラフを作成します。LCF表記法は立方ハミルトニアングラフの作成に用いられます。
詳しい説明は以下を参照してください。
http://mathworld.wolfram.com/LCFNotation.html
例1($K_{3,3}$)
G = nx.LCF_graph(6, [3, -3], 3)
pos=nx.circular_layout(G)
plt.cla()
nx.draw_networkx(G,pos)
plt.show()
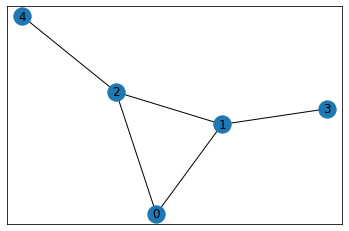
bull_graph(ブルグラフ)
bull_graph(create_using=None)
ブル(雄牛)グラフを返します。このグラフは1つの三角形とそれにつながる2個の連結でないノードから構成されています。
G=nx.bull_graph()
plt.cla()
nx.draw_networkx(G)
plt.show()
chvatal_graph(フバータルグラフ)
chvatal_graph(create_using=None)
フバータルグラフを返します。
cubical_graph(立方体グラフ)
cubical_graph(create_using=None)
3-正則の正六面体グラフを返します。
G=nx.cubical_graph()
plt.cla()
nx.draw_networkx(G)
plt.show()
desargues_graph(デザルググラフ)
desargues_graph(create_using=None)
デザルググラフを返します。
G=nx.desargues_graph()
plt.cla()
pos=nx.circular_layout(G)
nx.draw_networkx(G,pos)
plt.show()
diamond_graph(ダイヤモンドグラフ)
diamond_graph(create_using=None)
ダイヤモンドグラフを返します。
dodecahedral_graph(正十二面体グラフ)
dodecahedral_graph(create_using=None)
正十二面体グラフを返します。
frucht_graph(フレフトグラフ)
frucht_graph(create_using=None)
フレフトグラフを返します。このグラフは、対称性を持たない最小のキュービタルグラフの一つです。自己同型群は単位元のみで構成されます。
heawood_graph(ヒーウッドグラフ)
heawood_graph(create_using=None)
ヒーウッドグラフを返します。
hoffman_singleton_graph(ホフマンーシングルトングラフ)
hoffman_singleton_graph()
ホフマンーシングルトングラフを返します。
もっときれいにグラフを書くと五芒星が見えます。
https://mathworld.wolfram.com/Hoffman-SingletonGraph.html
house_graph(ハウスグラフ)
house_graph(create_using=None)
家型のグラフを返します。
house_x_graph(ハウスXグラフ)
house_x_graph(create_using=None)
家型のグラフの四角部分にXが加わったグラフを返します。
icosahedral_graph(正二十面体グラフ)
icosahedral_graph(create_using=None)
正二十面体グラフを返します。
krackhardt_kite_graph(クラックハートのカイトグラフ)
krackhardt_kite_graph(create_using=None)
Krackhardtのカイト(凧)グラフを返します。このグラフはDavid Krackhardtによって導入された10人の俳優のソーシャルネットワークです。伝統的なラベルはAndre=1, Beverley=2, Carol=3, Diane=4, Ed=5, Fernando=6, Garth=7, Heather=8, Ike=9, Jane=10です。
moebius_kantor_graph(メビウスーカントールグラフ)
moebius_kantor_graph(create_using=None)
メビウスーカントールグラフを返します。
octahedral_graph(八面体グラフ)
octahedral_graph(create_using=None)
八面体グラフを返します。
pappus_graph(パップスグラフ)
pappus_graph()
パップスグラフを返します。
petersen_graph(ピーターセングラフ)
petersen_graph(create_using=None)
ピーターセングラフを返します。
sedgewick_maze_graph(セッジウィック迷路グラフ)
sedgewick_maze_graph(create_using=None)
以下の文献を参考にした迷路グラフを返します。ノードは0~7でラベル付けされます、
Sedgewick,3rd Edition, Part 5, Graph Algorithms, Chapter 18,
tetrahedral_graph(四面体グラフ)
tetrahedral_graph(create_using=None)
3-正則の正四面体グラフを返します。
truncated_cube_graph(切頂立方体グラフ)
truncated_cube_graph(create_using=None)
切頂立方体(角をとったサイコロ様)グラフを返します。
truncated_tetrahedron_graph(切頂四面体グラフ)
truncated_tetrahedron_graph(create_using=None)
切頂四面体グラフを返します。
tutte_graph(タットグラフ)
tutte_graph(create_using=None)
タットグラフを返します。
Social Networks(ソーシャルネットワーク)
有名なソーシャルネットワークグラフです。
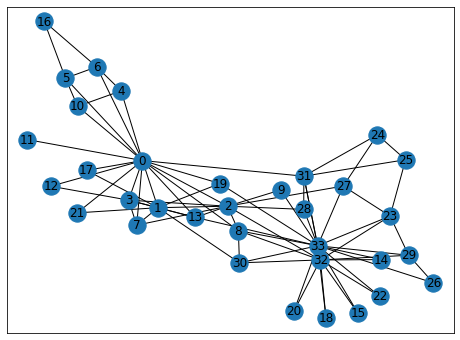
karate_club_graph(Zacharyの空手クラブ)
karate_club_graph()
アメリカの社会心理学者Zacharyが調査した空手クラブのメンバー間のネットワークです。ノード0とノード32,33を中心とする2つの派閥に分かれていることがわかります。
Zachary, Wayne W. “An Information Flow Model for Conflict and Fission in Small Groups.” Journal of Anthropological Research, 33, 452–473, (1977).
G=nx.karate_club_graph()
plt.figure(figsize=(8,6))
nx.draw_networkx(G)
plt.show()
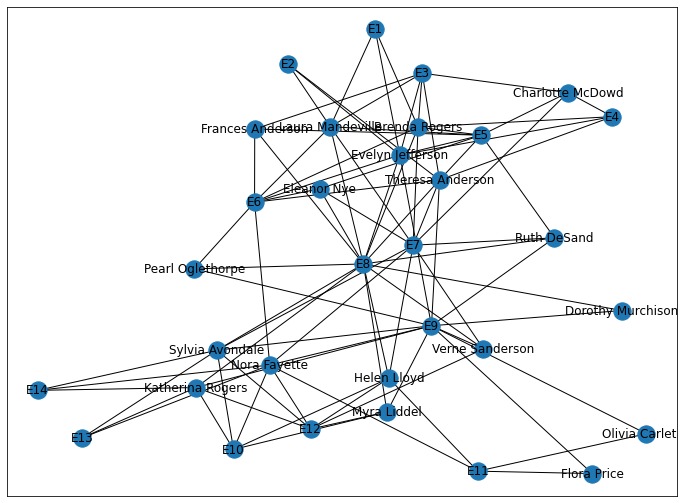
davis_southern_women_graph(Davisらの南部女性グラフ)
davis_southern_women_graph()
1930年代にDavisらによって調査されたアメリカ南部の女性18人のネットワークです。女性を表す18個のノードと参加したイベントを表す14個のノードから構成される2部グラフです。
A. Davis, Gardner, B. B., Gardner, M. R., 1941. Deep South. University of Chicago Press, Chicago, IL.
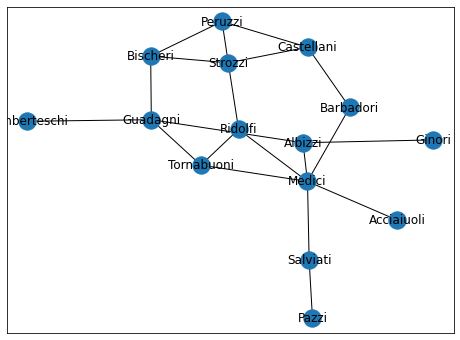
florentine_families_graph(フィレンツェの家族)
florentine_families_graph()
ルネサンス期フィレンツェにおけるメディチ家などの有力家の婚姻関係です。
Ronald L. Breiger and Philippa E. Pattison Cumulated social roles: The duality of persons and their algebras,1 Social Networks, Volume 8, Issue 3, September 1986, Pages 215-256
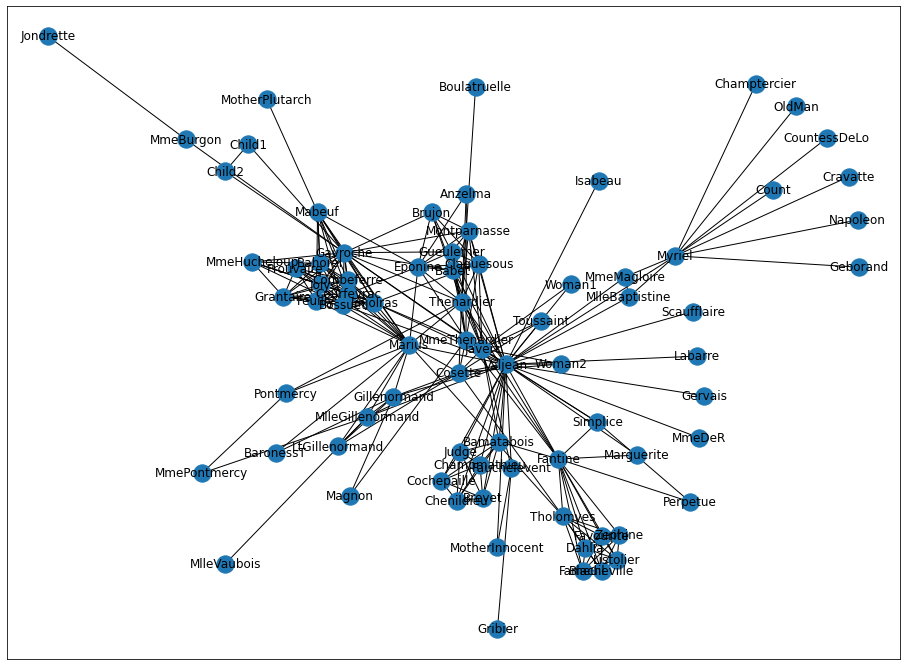
les_miserables_graph()
les_miserables_graph()
小説「レ・ミゼラブル」の登場人物のグラフです。
D. E. Knuth, 1993. The Stanford GraphBase: a platform for combinatorial computing, pp. 74-87. New York: AcM Press.