Go to Qiita Advent Calendar 2024 Top
LoginSignup
6
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@STInverSpinel

2次元Turingパターンの生成

Last updated at Posted at 2018-06-05
  • 2次元チューリングパターン(two-dimensional Turing pattern)をシミュレートする
  • 陽解法と陰解法

##考える系
2次元の平面組織を考え、これを$dx$ごとに離散化します。平面組織が正方形であり１辺の長さが1であるとすると、$(1/dx)×(1/dx)$個の領域に離散化されます。また、時間も$dt$ごとに離散化され、時刻$t$は$m×dt(mは整数)$のみをとるものとします。

##反応項

領域内では、活性因子(Activator)と抑制因子(Inhibitor)が産生されます。上から$x$行目左から$y$番目の領域における、ある時刻$t$のときの、活性因子と抑制因子の濃度をそれぞれ$p(x$,$y$,$t)$,$q(x$,$y$,$t)$と表します。これはまた$(1/dx)×(1/dx)$の正方行列$p(t)$,$q(t)$とも表します。

活性因子は、因子の産生を促進します。抑制因子は、因子の産生を抑制します。詳しくは以下の表のように定義されます。

　 活性因子によって 抑制因子によって
活性因子の産生は 促進される(+0.6) 抑制される(-1.0)
抑制因子の産生は 促進される(+1.5) 抑制される(-2.0)

また、活性因子はある程度の濃度以上になると自身の濃度の3乗で産生が抑制されます。

これら産生量の変化は以下の関数で示されます。

\begin{align}
f(p,q)&=+0.6p-1.0q-p^3\\
g(p,q)&=+1.5p-2.0q
\end{align}

##陽解法

###拡散項
境界条件：周期境界条件

p(x,y,t+dt)=p(x,y,t)+\Biggl(f(p(x,y,t),q(x,y,t))+\frac{d_p}{dx^2}\Bigl(p(x+dx,y,t)+p(x-dx,y,t)+p(x,y+dy,t)+p(x,y-dy,t)-4p(x,y,t)\Bigr)\Biggr)dt\\
q(x,y,t+dt)=q(x,y,t)+\Biggl(g(p(x,y,t),q(x,y,t))+\frac{d_q}{dx^2}\Bigl(q(x+dx,y,t)+q(x-dx,y,t)+q(x,y+dy,t)+q(x,y-dy,t)-4q(x,y,t)\Bigl)\Biggr)dt

ここで、$d_p,d_q$はそれぞれ活性因子、抑制因子の拡散係数。

###計算
初期濃度にはrand()を使ってある程度の揺らぎを与えておく。

using Plots
gr()

dx=0.04
dt=0.02
N=convert(Int,1/dx)

dp=0.0002
dq=0.01

pInitial=rand(N,N)*0.01
qInitial=rand(N,N)*0.01

f(p,q)=0.6*p-q-p.^3
g(p,q)=1.5*p-2*q

diffusion(v)=circshift(v,1)+circshift(v,-1)-2*v+circshift(v,(0,1))+circshift(v,(0,-1))-2*v
diffusionP(v)=dp*diffusion(v)/(dx*dx)
diffusionQ(v)=dq*diffusion(v)/(dx*dx)

function pqAfterDt(p,q)
    p=p+dt*(f(p,q)+diffusionP(p))
    q=q+dt*(g(p,q)+diffusionQ(q))
    return p,q
end

p=pInitial
q=qInitial

#to t=60
anim = @animate for m=0:3000
    t=round(m*dt,3)
    heatmap(p,
        title="t = $t ",
        aspect_ratio=:equal
        )
    p,q=pqAfterDt(p,q)
end every 25
@time gif(anim,"tmp/6_6_2D_pattern.gif",fps=4)

54.561467 seconds (1.40 k allocations: 49.469 KiB)

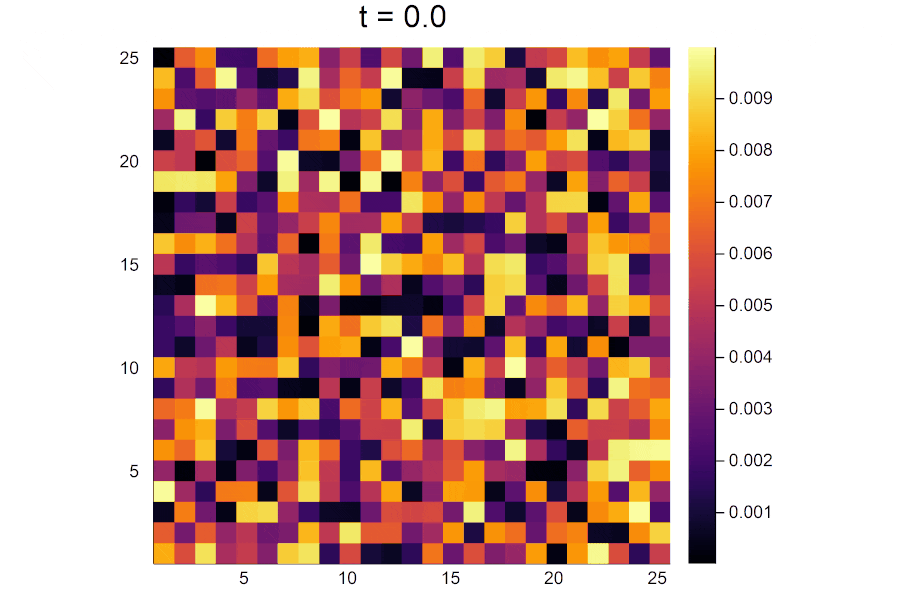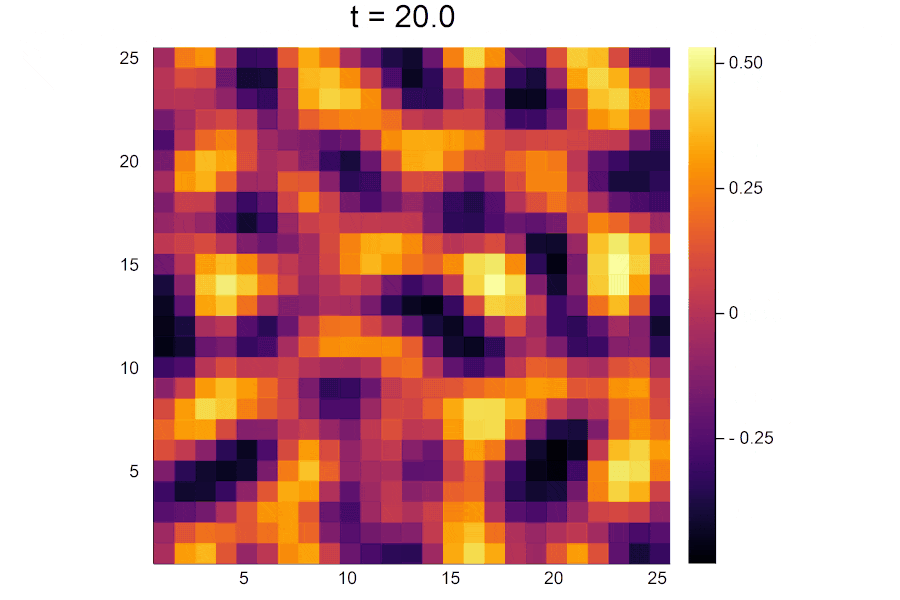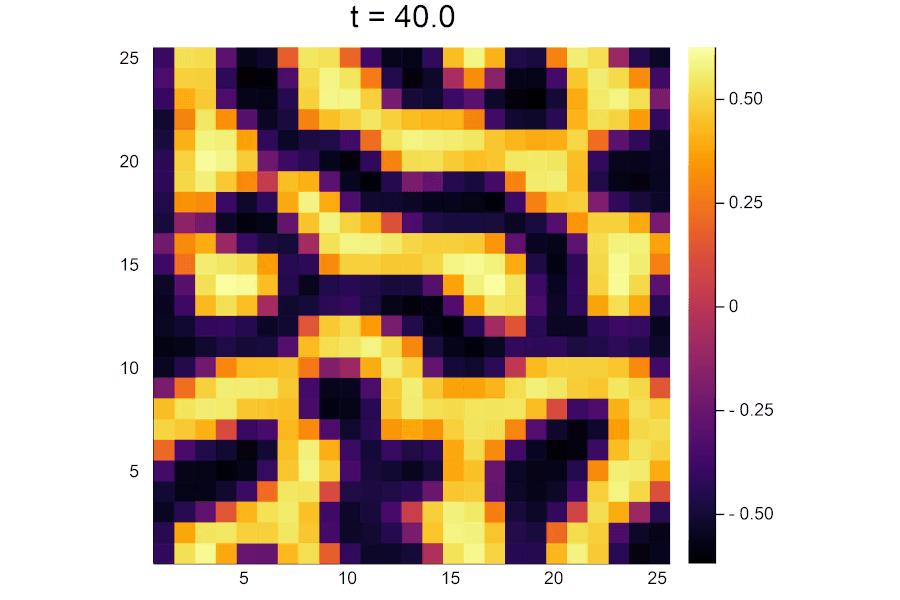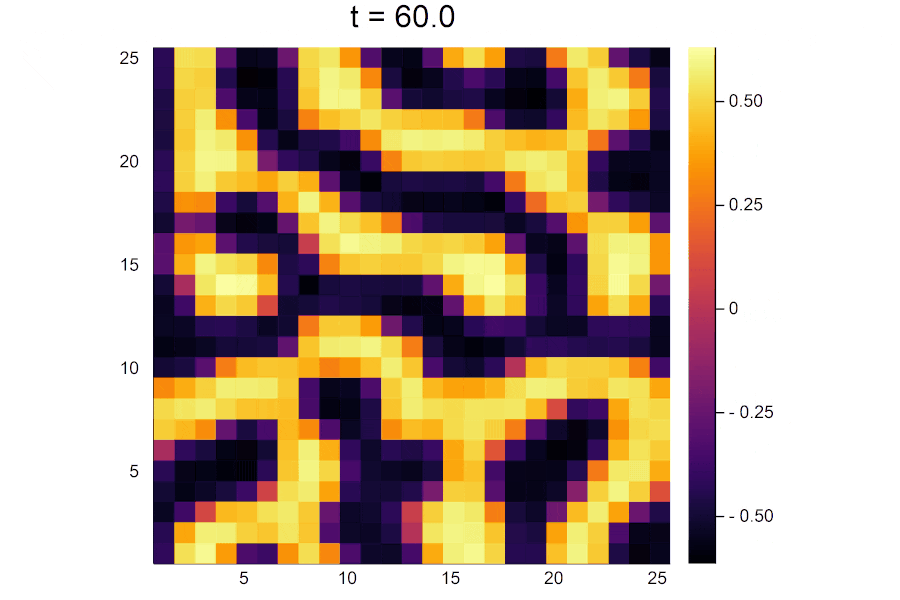
6_6_2D_pattern_min.gif

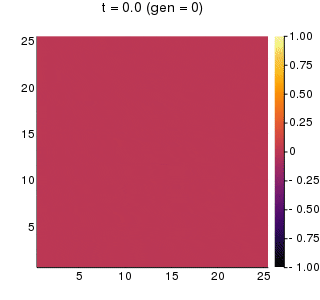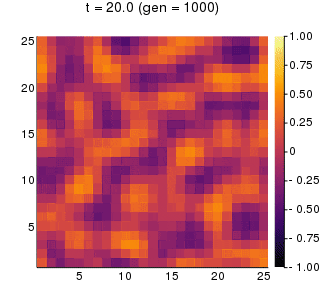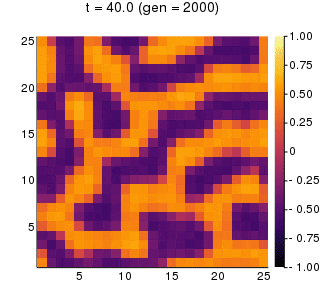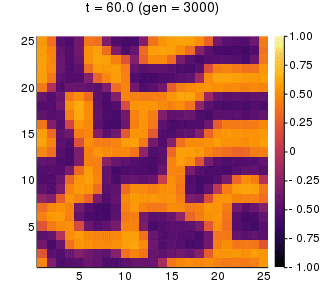
時間がたつにつれて活性因子の濃淡がはっきりと分かれていき、パターンが形成されていく様子が見えます。

##陰解法

###陰解法のスキーム
活性因子、抑制因子の濃度をそれぞれ$u,v$で表す（$p,q$ではなく）。

u(x,y,t+dt)=u(x,y,t)+\frac{d_p}{dx^2}\Bigl(u(x+dx,y,t+dt)+u(x-dx,y,t+dt)+u(x,y+dy,t+dt)+u(x,y-dy,t+dt)-4u(x,y,t+dt)\Bigr)dt\\
v(x,y,t+dt)=v(x,y,t)+\frac{d_q}{dx^2}\Bigl(v(x+dx,y,t+dt)+v(x-dx,y,t+dt)+v(x,y+dy,t+dt)+v(x,y-dy,t+dt)-4v(x,y,t+dt)\Bigr)dt

ここで

k=
\left(
\begin{array}{ccccc}
1+4\frac{d_p}{dx^2}dt & -\frac{d_p}{dx^2}dt & \cdots & 0 & -\frac{d_p}{dx^2}dt\\
-\frac{d_p}{dx^2}dt & 0 & \cdots & 0 & 0 \\
\vdots & & \ddots & & \vdots \\
0 & 0 & \cdots & 0 & 0 \\
-\frac{d_p}{dx^2}dt & 0 & \cdots & 0 & 0
\end{array}
\right)

というカーネル$k$を作れば、活性因子の支配方程式は$u(x,y,t)$の分布を表す行列$u(t)$を使って

k \otimes u(t+dt) = u(t)

という畳み込み式になる（$\otimes$は畳み込みを表す）、これを畳み込み定理よりフーリエ変換の積で表す。

F(k)\circ F(u(t+dt))=F(u(t))\\
F(u(t+dt))=\frac{F(u(t))}{F(k)}\\
u(t+dt)=IF\Bigl(\frac{F(u(t))}{F(k)}\Bigr)

$F(),IF()$はそれぞれフーリエ変換、逆フーリエ変換を表し、$\circ$は要素ごとの積を表す（多分）。

###計算

using Plots
gr()

dx=0.04
N=convert(Int,1/dx) #gridSize=25

dt=0.02
dp=0.0002
dq=0.01

f(u,v)=u+dt*(0.6*u-v-u.^3)
g(u,v)=v+dt*(1.5*u-2*v)

kernelU=zeros(N,N)
kernelU[1,1]=1+4*dt*dp/dx/dx
kernelU[2,1]  =-dt*dp/dx/dx
kernelU[end,1]=-dt*dp/dx/dx
kernelU[1,end]=-dt*dp/dx/dx
kernelU[1,2]  =-dt*dp/dx/dx

kernelV=zeros(N,N)
kernelV[1,1]=1+4*dt*dq/dx/dx
kernelV[2,1]  =-dt*dq/dx/dx
kernelV[end,1]=-dt*dq/dx/dx
kernelV[1,end]=-dt*dq/dx/dx
kernelV[1,2]  =-dt*dq/dx/dx

ku=1./(fft(kernelU))
kv=1./(fft(kernelV))

function oneStep(u,v)
    u=ifft(ku.*fft(f(u,v)))
    v=ifft(kv.*fft(g(u,v)))
    return u,v
end

uI=rand(N,N)*0.01
vI=rand(N,N)*0.01

u=uI
v=vI

#to t=60
anim = @animate for m in 0:3000
    t=round(m*dt,3)
    heatmap(real(u),
        title="t = $t",
        aspect_ratio=:equal
    )
    u,v=oneStep(u,v)
end every 25
@time gif(anim,"tmp/6_6_2D_pattern_inkaihou.gif",fps=4)

50.064059 seconds (1.33 k allocations: 47.438 KiB)
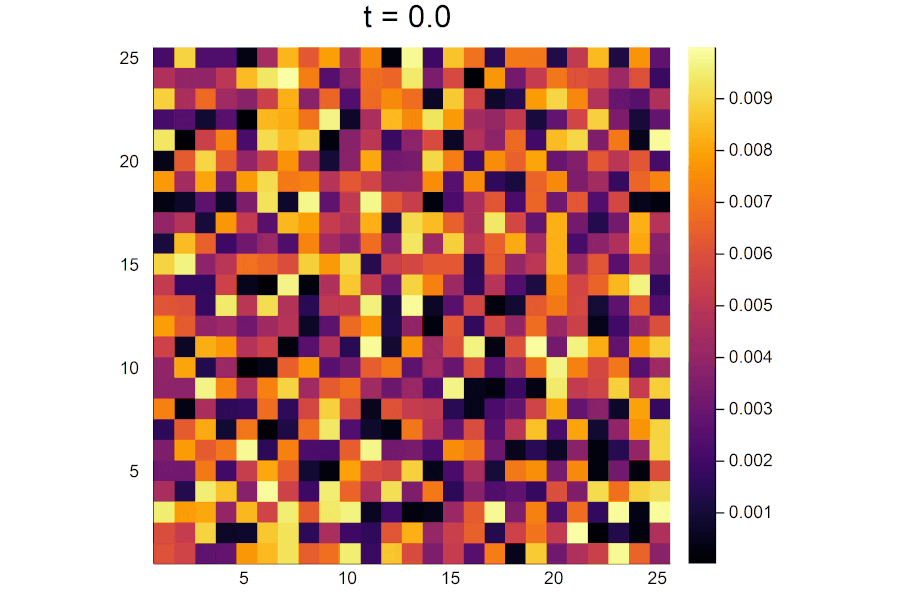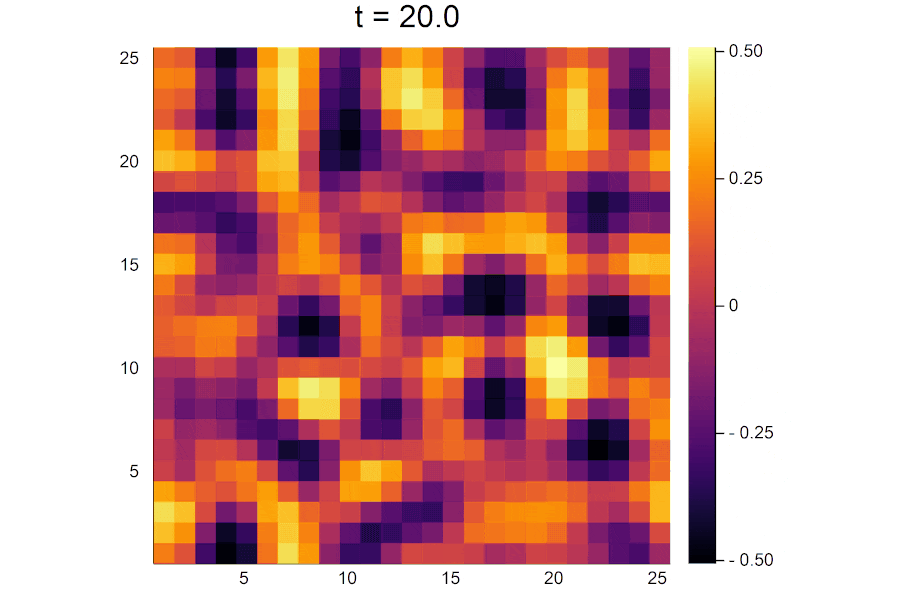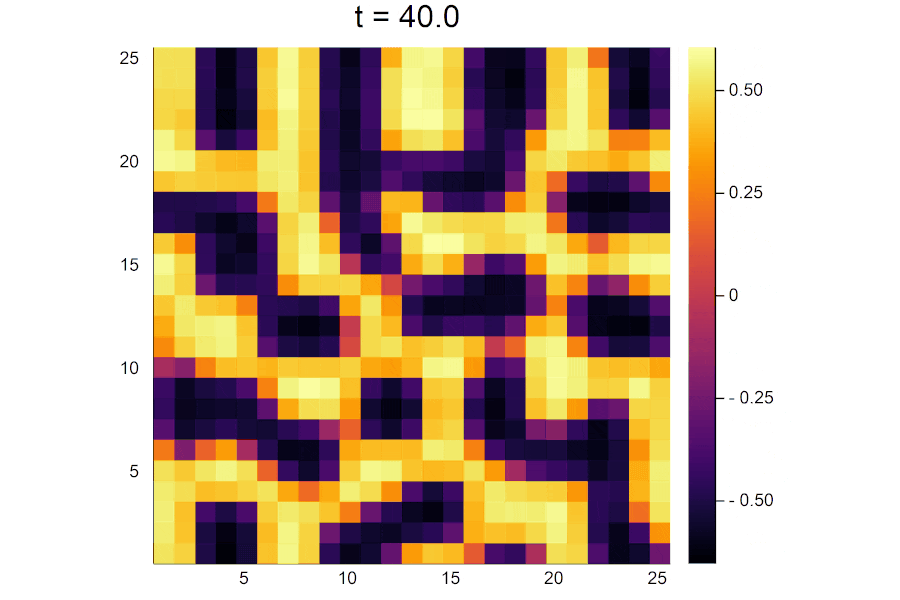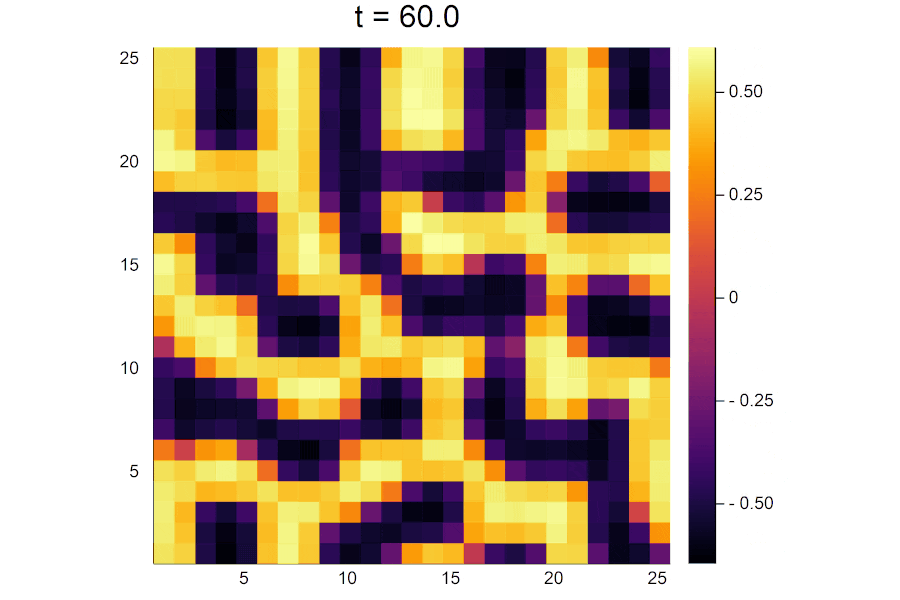
6_6_2D_pattern_inkaihou_min.gif

陽解法と比較してパターンの形が異なるのは、ランダムに決められた初期濃度が実行するたびに異なるためです。

##つまずいたところ

  • 行列どうしの掛け算で、要素ごとの積にしなければいけないところをふつうの積にしていた。すなわちA.*BとかかなければいけないところをA*Bと書いていた。スカラー同士やスカラーと行列の掛け算は*で済むのでコードの可読性が悪くなりやすい。
  • 参考文献の「発生の数理」p.130の(6.70)式は(end,1)成分と(end,end)成分が逆。あと反応項の正負が反対（移項前の状態）。
  • フーリエ変換の前後で規格化係数がかかったりかからなかったりする。
  • フーリエ変換するライブラリにはFFTWとFFTVIewsがあるけど後者はよく分からなかった。

##書き直したバージョン(20180926追記)

  • 陰解法のコードをJulia　v1.0用に書き直した。
  • moduleとstructを使い高速化。
  • 図のカラーバーの上限下限を(-1.0,1.0)に固定。なのでちょっと見え方が違う。
  • C言語風にmain()で開始。
  • 追加が必要なパッケージ：FFTW,Plots
#2D-Turing pattern陰解法
#参考：三浦岳、発生の数理、京都大学学術出版会、2015、6.6
#julia v1.0

using FFTW
using Random
using Plots
gr(size=(320,300),titlefont=font("sans-serif",9))

Random.seed!(1234)

module TuringPattern
    struct Param
        #セル個数
        N::Int64
        #単位時間
        dt::Float64
        #活性因子、抑制因子の拡散係数
        dp::Float64
        dq::Float64
        #カーネルをフーリエ変換し、要素ごとの逆数をとったもの
        ku::Array{ComplexF64,2}
        kv::Array{ComplexF64,2}
        #開始世代、終了世代数
        mmin::Int64
        mmax::Int64
    end
    mutable struct Variables
        #活性因子、抑制因子の濃度
        u::Array{ComplexF64,2}
        v::Array{ComplexF64,2}
    end
end


dx=0.04
N=convert(Int64,1/dx) #gridSize=25

dt=0.02
dp=0.0002
dq=0.01

kernelU=zeros(N,N)
kernelU[1,1]  =1+4*dt*dp/dx/dx
kernelU[2,1]  =-dt*dp/dx/dx
kernelU[end,1]=-dt*dp/dx/dx
kernelU[1,end]=-dt*dp/dx/dx
kernelU[1,2]  =-dt*dp/dx/dx

kernelV=zeros(N,N)
kernelV[1,1]  =1+4*dt*dq/dx/dx
kernelV[2,1]  =-dt*dq/dx/dx
kernelV[end,1]=-dt*dq/dx/dx
kernelV[1,end]=-dt*dq/dx/dx
kernelV[1,2]  =-dt*dq/dx/dx

ku=1 ./(fft(kernelU))
kv=1 ./(fft(kernelV))

mmin=0
mmax=3000


param1=TuringPattern.Param(N,dt,dp,dq,ku,kv,mmin,mmax)

u=rand(N,N)*0.01
v=rand(N,N)*0.01

var1=TuringPattern.Variables(u,v)

f(param,var)=var.u.+param.dt.*(0.6*var.u-var.v-var.u.^3)
g(param,var)=var.v.+param.dt.*(1.5*var.u-2.0 .*var.v)

function oneStep(param,var)
    var.u=ifft(param.ku.*fft(f(param,var)))
    var.v=ifft(param.kv.*fft(g(param,var)))
end

function draw(param,var,m)
    t=round(m*param.dt,digits=2)
    heatmap(real(var.u),
        title="t = $t (gen = $m)",
        cbarlims=(-1.0,1.0),
        aspect_ratio=:equal
    )
end

function main(param,var)
    @time anim = @animate for m in mmin:mmax  
        draw(param,var,m)
        oneStep(param,var)
    end every 25
    @time gif(anim,"tmp/6_6_2D_pattern_inkaihou_320_10.gif",fps=4)
end

main(param1,var1)

9.550606 seconds (38.63 M allocations: 1.801 GiB, 6.52% gc time)
0.815474 seconds (714 allocations: 39.531 KiB)

6_6_2D_pattern_inkaihou_320_10.gif

##参考文献
三浦岳、発生の数理、京都大学学術出版会、初版、pp91-142、2015

6
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?