統計検定2級覚え書き（後半）

統計検定2級覚え書き（前半）

7. 確率モデルの導入

7-1. 確率

事象と確率

計算問題は解いて覚える。

【過去問】
2021年6月の問9（誕生日のパラドックス）
2019年11月の問8
2018年11月の問7
2018年6月の問7

加法定理

P(A\cup B)=P(A)+P(B)-P(A \cap B)

Bを条件とするAの条件付確率

他の事象Bが起こったとわかっている場合に、事象Aの起こる確率。

P(A|B)=\frac{P(A\cap B)}{P(B)}

独立と排反

下記が成り立つことはAとBは独立であることに等しい

P(A\cap B)=P(A) \cdot P(B)

下記が成り立つことはAとBは排反であることに等しい

P(A\cap B) \neq 0

【過去問】
2019年度6月の問7

ベイズの定理

P(H_i|A)=\frac{P(H_i) \cdot P(A|H_i)}{\sum_{j=1}^N P(H_j) \cdot P(A|H_j)}

例：ある部品を工場1と工場2から仕入れている。部品の70%は工場1で、30%は工場2で生産している。工場1で不良品が出る確率は2%、工場2で不良品が出る確率を1%である。今、ある部品が不良品であったとき、その部品が工場1で生産された確率は？

P(H_i|A)=\frac{P(H_1) \cdot P(A|H_1)}{P(H_1) \cdot P(A|H_1) + P(H_2) \cdot P(A|H_2) }\\
=\frac{0.70 \times 0.02}{0.70 \times 0.02 + 0.30 \times 0.01}\\
=0.82

$H_1$：部品が工場1で生産された（原因）
$H_2$：部品が工場2で生産された（原因）
$A$：部品が不良品である（結果）
$P(H_1)$：部品が工場1で生産された確率（事前確率）
$P(H_2)$：部品が工場2で生産された確率（事前確率）
$P(A|H_1)$：工場1で生産された部品に対し、それが不良品である確率
$P(A|H_2)$：工場2で生産された部品に対し、それが不良品である確率
$P(H_1|A)$：部品が不良品であるとき、それが工場1で生産された確率

【過去問】
2017年11月の問7

7-2. 確率変数

確率密度関数

$f(x)$で表される。$f(x) \geq 0$かつ$\int_{-\infty}^{\infty}f(x)dx=1$を満たす。

分布関数（累積確率密度関数）

$F(x)$で表される。$x$で微分すると$f(x)$になる。

【過去問】
2019年11月の問10

確率変数の平均（期待値）

E[X]=\int_{-\infty}^{+\infty} x f(x) dx \text{（連続型）}\\
E[X]=\sum_{i=1}^n x_i p_i \text{（離散型）}

もっと詳しく

【過去問】
2019年11月の問9

確率変数の分散

V[X]=E[X^2]-(E[X])^2

【過去問】
2017年11月の問8

期待値の性質

\begin{align}
E[c]&=c\\
E[X+c]&=E[X]\\
E[cX]&=cE[X]
\end{align}

ここで$c$は定数である。

期待値の加法性

確率変数X,Yが互いに独立であろうがなかろうが、期待値の加法性は成り立つ。

E[X+Y]=E[X]+E[Y]

もっと詳しく

統計学入門p.96

分散の性質

\begin{align}
V[c]&=0\\
V[X+c]&=V[X]\\
V[cX]&=c^2V[X]
\end{align}

ここで$c$は定数である。

分散の加法性

X,Yが独立である場合、分散は加法性をもつ。

V[X \pm Y]=V[X]+V[Y]\\
(\sigma_{X \pm Y}^2=\sigma_X^2+\sigma_Y^2)

X,Yが独立でない場合、分散は加法性をもたない。全体を2乗展開した式で計算する。

V[X+Y]=V[X]+2\mathrm{Cov}[X,Y]+V[Y]\\
V[2X-Y]=4V[X]-4\mathrm{Cov}[X,Y]+V[Y]\\
V[X+Y+Z]=V[X]+V[Y]+V[Z]+2\mathrm{Cov}[X,Y]+2\mathrm{Cov}[Y,Z]+2\mathrm{Cov}[Z,X]

もっと詳しく

統計学入門p.97-98,148

【過去問】
2018年6月の問8[2]

確率変数の和と差（同時分布、和の期待値・分散）

2変数の共分散・相関

分散$V[X]$と確率変数の2乗の期待値$E[X^2]$の関係式

V[X]=E[X^2]-(E[X])^2

共分散$\mathrm{Cov}[X,Y]$と確率変数の積の期待値$E[XY]$の関係式

\mathrm{Cov}[X,Y]=E[XY]-E[X]E[Y]

相関係数$r[X,Y]$と共分散$\mathrm{Cov}[X,Y]$の関係式

r[X,Y]=\frac{ \mathrm{Cov}[X,Y]}{\sqrt{V[X]}\sqrt{V[Y]}}

互いに無相関な標準化された変数$X_1,X_2,X_3$があったとき、そのどれかひとつと標本平均$(X_1+X_2+X_3)/3$の共分散

Cov[X_1,\frac{X_1+X_2+X_3}{3}]=\frac{1}{3}(Cov[X_1,X_1]+Cov[X_1,X_2]+Cov[X_1,X_3])

【過去問】
2021年6月の問5
2019年6月の問2[1]
2019年6月の問9
2018年6月の問9
2016年11月の問8

7-3. 確率分布

ベルヌーイ試行

2種類の可能な結果がある（成功と失敗など）。
片方が起きる確率は$p$,もう片方が起きる確率は$1-p$で表される。
前後の結果が試行に影響を与えることはない（独立である）。

二項分布

確率$p$で成功するベルヌーイ試行を$n$回繰り返すとき$x$回成功する確率分布

\begin{align}
f(x)&= {}_nC_x p^x (1-p)^{n-x}\\
E[X]&=np\\
V[X]&=np(1-p)
\end{align}

【過去問】
2018年11月の問9
2018年11月の問15[1]

幾何分布

確率$p$のベルヌーイ試行を最初の成功が出るまで繰り返すときの確率分布

\begin{align}
f(x)&=p (1-p)^x-1\\
E[X]&=1/p\\
V[X]&=(1-p)/p^2
\end{align}

【過去問】
2019年度6月問10

ポアソン分布

二項分布を$n\rightarrow \infty, p \rightarrow 0$にとばしたときの分布。まれにおこる事象についてあてはまる。$np \rightarrow \lambda$となる$\lambda$をおくと

f(x)=\frac{e^{-\lambda}\lambda^x}{x!} \; (x=0,1,2,\cdots)\\
E[X]=\lambda\\
V[X]=\lambda

【過去問】
2017年11月の問11

一様分布

f(x)=\left\{
\begin{array}{ll}
0 & (x<l)\\
\frac{1}{r-l} & (l \leq x \leq r)\\
0 & (r<x)\\
\end{array}
\right.

E[X]=\frac{l+r}{2}\\
V[X]=\frac{(r-l)^2}{12}

【過去問】
2021年6月の問11

8. 推測

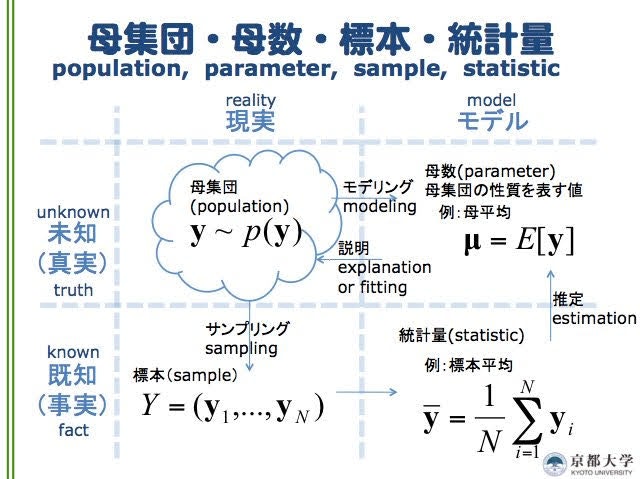
まず、母集団と標本の関係性をざっくりと把握しておく。

画像は下記ツイートより引用（一番わかりやすかった）。

受講生のコメントに「（真実・事実）×（現実・モデル）4分割の表に感動した。学部2回生の統計の講義で見たかった」とあった、
ぼくとしても最高のお気に入りになってる渾身のスライドがこちらになります。 pic.twitter.com/X2ajmXkg7p

— shigepong (@shigepong) April 13, 2017

8-1. 標本分布

標本平均の期待値・分散

確率変数$X_1, X_2, \cdots, X_n$は互いに独立で期待値が$\mu$、分散が$\sigma^2$であるとする。標本平均$\bar{X}=\frac{\sum_{i=1}^n X_i}{n}$の期待値と分散はそれぞれ

E[\bar{X}]=\mu\\
V[\bar{X}]=\frac{\sigma^2}{n}

である。

【過去問】
2018年11月の問10

チェビシェフの不等式

P(|\bar{X}-\mu| \geq \epsilon) \leq \frac{\sigma^2}{\epsilon^2}

【過去問】
2021年6月の問12

中心極限定理

母集団分布が何であっても、標本が十分に大きい場合は標本平均の分布は正規分布に従う。

【過去問】
2019年11月の問14

標準化変数

Z=\frac{\bar{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}

カイ二乗分布

$Z_1,Z_2, \cdots, Z_k$を互いに独立で、標準正規分布N(0,1)に従う確率変数とする。下式で表される確率変数$\chi^2$を従う確率分布を自由度$k$のカイ二乗分布という。

\chi^2=Z_1^2+Z_2^2+\cdots+Z_k^2

t分布

2つの確率変数Y,Zが次の条件を満たす。

1. Zは標準正規分布N(0,1)に従う。
2. Yは自由度kのカイ二乗分布$\chi^2(k)$に従う。
3. ZとYは独立である。

このとき、下式で定義される確率変数tが従う確率分布を自由度kのt分布（スチューデントのt分布）という。

t=\frac{Z}{\sqrt{\frac{Y}{k}}}

スチューデントのt統計量

t=\frac{\bar{X}-\mu}{\sqrt{\frac{S^2}{n}}}

F分布

2つの確率変数U,Vが次の条件を満たす。

1. Uは自由度$k_1$のカイ二乗分布$\chi^2(k_1)$に従う。
2. Vは自由度$k_2$のカイ二乗分布$\chi^2(k_2)$に従う。
3. UとVは独立である。

このとき、下式で定義されるF（フィッシャーの分散比）が従う確率分布を自由度$(k_1,k_2)$のF分布という。

F=\frac{U/k_1}{V/k_2}

標準正規分布表（付表１）の利用

正規分布におけるある範囲内の確率の計算

標準正規分布（平均$\mu=0$、分散$\sigma^2=1$の正規分布）でないと標準正規分布表は使えないことに注意。標準正規分布でない正規分布が与えられた場合は、あらかじめ式変形するなり$Z=\frac{X-\mu}{\sigma}$で標準正規分布に変換しておくなりする。

境界値が負の場合は正に置き換えて付表１をみる
$\Phi(-z)=1-\Phi(z)$
$Q(-z)=1-Q(z)$

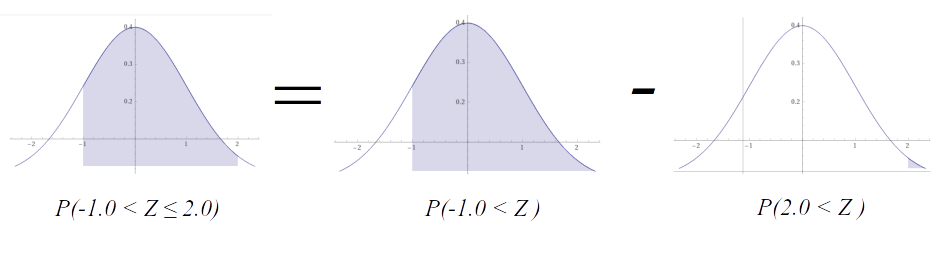
例：$P(L < X \leq U)$の計算

\begin{align}
P(-1.0 < Z \leq 2.0)&=P(-1.0<Z)-P(2.0<Z)\\
&=Q(-1.0)-Q(2.0)\\
&=1-Q(1.0)-Q(2.0)\\
&=1-0.1587-0.0228\\
&=0.8185
\end{align}

【過去問】
2019年6月の問11
2018年11月の問8
2018年6月の問8[1]
2018年6月の問10[1]
統計学入門p195

t分布のパーセント点（付表2）を使った確率計算

両側検定のときは$\alpha$を2倍して考える。

【過去問】
2019年度6月の問12

標本平均の標準誤差

平均$\mu$、標準偏差$\sigma$をもつ$n$個の確率変数の標本平均では標準誤差$se$を使って標準化変数$Z$を計算する。

se(\bar{X})=\frac{\sigma}{\sqrt{n}}\\

Z=\frac{\bar{X}-\mu}{se(\bar{X})}

【過去問】
2019年11月の問7
2017年11月の問10

標本平均の変動係数

母集団の平均を$\mu$、標準偏差$\sigma$とおく。その中から$n$個を無作為抽出したとき平均の変動係数

C.D.=\frac{\sqrt{\frac{\sigma^2}{n}}}{\mu}

8-2. 推定

推定とは統計量から母数がどれくらいの区間に存在するのか見積もる行為。

一致性

標本サイズ$n$が大きくなるほど、推定量$\hat{\theta}$が真の母数の値$\theta$に近づく性質。この性質を満たす推定量を一致推定量という。

不偏性

標本サイズ$n$にかかわらず、推定量の期待値$E[\hat{\theta}]$が真の母数の値$\theta$となる性質。

もっと詳しく

統計学入門p.220

【過去問】
2019年11月の問12

1つの正規母集団における母平均の区間推定（母分散未知）

標本サイズ$n$, 標本平均$\bar{X}$, 不偏分散$S^2$のみわかっている場合、母平均$\mu$の95%信頼区間は

\bar{X}\pm t_{0.025}(n-1) \sqrt{\frac{S^2 }{n}}

$t_{0.025}(n-1)$は付表2から$\nu=n-1, \alpha=0.025$の交点の値を使う。

もっと詳しく

【過去問】
2019年6月の問15
2018年6月の問10[2]

1つの正規母集団における母比率の区間推定（母比率の95%信頼区間）

よく出る。

正規分布において、抽出したサンプルサイズを$n$, 標本比率を$\hat{p}$とおくとき、母比率$p$の95%信頼区間は

\hat{p}\pm 1.96 \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}

1.96という数字を忘れても、標準正規分布の上側確率の表（付表１）からQ(u)=0.0250(2.5%)となるuを探せば良い。
信頼区間は$\hat{p}=0.5$のとき最大。

もっと詳しく

【過去問】
2019年11月の問13
2019年11月の問15
2019年6月の問14
2018年11月の問12
2018年6月の問11[1]
2017年11月の問13

2つの正規母集団における母比率の差の区間推定（95%信頼区間）

2つの正規母集団の標本比率を$\hat{p_1},\hat{p_2}$、標本サイズを$n_1,n_2$とおくとき、母比率の差の95%信頼区間は

\hat{p_1}-\hat{p_2} \pm 1.96 \sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}

8-3. 仮説検定

P-値

帰無仮説の条件下で、検定統計量がその値となる確率のこと。
例：$P(u \geq 1.95)$は統計検定量$u$が1.95以上となる確率を示す。

両側検定と片側検定

第１種の過誤と第２種の過誤

第一種の過誤、第二種の過誤 pic.twitter.com/Eb7f2RWVAW

— ガウス分布くん (@gaussbumpukun) May 18, 2021

第１種の過誤：帰無仮説$H_0$が正しいのに、それを棄却してしまうこと。
第２種の過誤：帰無仮説$H_0$が誤っているのに、それを採択してしまうこと。

第１種の過誤が起きる確率$\alpha(x_0)$

• 有意水準$\alpha$に等しい。
• P(帰無仮説における棄却域)

第２種の過誤が起きる確率$\beta(x_0)$

• $1-\beta$を検出力と呼ぶ。
• P(対立仮説における採択域)

計算例
対立仮説による分布が標準正規分布でない場合、平均$\theta$, 分散$\sigma^2$を使い標準化してから棄却域境界$z_0$を計算する。

z_0=\frac{X_0-\theta}{\sqrt{\sigma^2}}

ここで$\theta$は対立仮説での値を用いる。

付表１を使って$P(z \leq z_0)$を求める。

\beta=P(x \leq x_0)=P(z \leq z_0)

もっと詳しく

【過去問】
2019年6月の問16
2018年11月の問14
2018年6月の問13（離散型の確率分布）
2017年11月の問14

1つの母集団における母平均の検定

片側検定（母分散既知）

片側検定（母分散未知）

母平均を$\mu$とおく。

帰無仮説：$\mu=\mu_0$
対立仮説：$\mu \gt \mu_0$または$\mu \lt \mu_0$

標本サイズ$n$, 標本平均$\bar{X}$, 不偏分散$S^2$を使ってt統計量を計算する。ここで、$\bar{X},S^2$は「比較するデータ間の差」の標本平均と不偏分散である。$\mu$は帰無仮説の値（$\mu=\mu_0$)を使う。

t=\frac{\bar{X}-\mu}{\sqrt{\frac{S^2}{n}}}

計算したt統計量と付表2を比較して、t統計量のほうが外側にあれば帰無仮説は棄却できる、そうでなければ棄却できない。使うt分布の自由度は$n-1$。

もっと詳しく

統計学入門p.241

【過去問】
2019年11月の問16
2019年6月の問15
2017年11月の問14

両側検定（母分散既知）

両側検定（母分散未知）

【過去問】
2018年11月の問13

1つの母集団における母比率の検定

標本サイズ$n$が十分に大きい場合、下式より得られるz統計量は標準正規分布に従う。

z=\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}

ここで$\hat{p}$は標本比率、$p_0$は母比率である。

もっと詳しく

統計学入門p.250

【過去問】
2018年11月の問15[2]

2つの母集団における母平均の差の検定（分散未知であるが等分散）

2標本検定と呼ばれる。

互いに独立で同一の分布に従う2つの母集団がある。2つの母集団の分散は未知だが等しいとみなす。

母集団	母集団の平均	標本の大きさ	標本	標本平均	偏差平方和
1番目	$\mu_1$	$m$	$X_i$	$\bar{X}$	$\sum_{i-1}^m (X_i - \bar{X})^2$
2番目	$\mu_2$	$n$	$Y_i$	$\bar{Y}$	$\sum_{i-1}^n (Y_i - \bar{Y})^2$

帰無仮説：$\mu_1=\mu_2$
対立仮説：$\mu_1 \neq \mu_2$（両側）、$\mu_1 \gt \mu_2$または$\mu_1 \lt \mu_2$（片側）、

それぞれの不偏分散をもとめる。

S_1^2=\frac{\sum_{i-1}^m (X_i - \bar{X})^2}{m-1}\\

S_2^2=\frac{\sum_{i-1}^n (Y_i - \bar{Y})^2}{n-1}

合併した分散$s^2$を計算する。

\begin{align}
S^2&=\frac{\sum_{i-1}^m (X_i - \bar{X})^2+\sum_{i-1}^n (Y_i - \bar{Y})^2}{(m-1)+(n-1)}\\
&=\frac{(m-1)S_1^2+(n-1)S_2^2}{(m-1)+(n-1)}

\end{align}

2標本t統計量を求める。

t=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{S\sqrt{\frac{1}{m}+\frac{1}{n}}}

この2標本t統計量は帰無仮説$H_0:\mu_1=\mu_2$の下では

t=\frac{\bar{X}-\bar{Y}}{S\sqrt{\frac{1}{m}+\frac{1}{n}}}

であり、これを使う。

自由度$\nu=m+n-2$のt分布を使って検定をおこなう。

もっと詳しく

統計学入門p205-206

【過去問】
2018年6月の問12[1]

2つの母集団における母平均の差の検定（母分散未知で等しいかどうかもわからない）

Welch's test

2級の範囲からは応用的

2つの母集団における母分散の比の検定（等分散性の検定）

帰無仮説：$\sigma_1^2=\sigma_2^2$
対立仮説：$\sigma_1^2 \neq \sigma_2^2$

フィッシャーの分散比を計算しF分布から棄却するかどうか決める。

F=\frac{s_1^2}{s_2^2}

F分布の自由度は(1の標本サイズ-1,2の標本サイズ-1)。
有意水準5%、片側検定：$\alpha=0.05$
有意水準5%、両側検定：$\alpha=0.025$

もっと詳しく
統計学入門p.244

【過去問】
2018年11月の問14
2018年6月の問16

2つの母集団における母比率の差の検定

2つの母集団に対し、それぞれ母比率を$p_1,p_2$、標本サイズを$n_1,n_2$、標本比率を$\hat{p_1}, \hat{p_2}$とおく。

帰無仮説：$p_1-p_2=0$
対立仮説：$p_1-p_2 \neq 0$

$n_1,n_2$が十分に大きい場合、下式のz統計量は標準正規分布に従う。

z=\frac{\hat{p_1}-\hat{p_2}}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})\hat{p}(1-\hat{p})}}

ここで

\hat{p}=\frac{n_1 \hat{p_1}+n_2 \hat{p_2}}{n_1+n_2}

もっと詳しく

統計学入門p.255

【過去問】
2018年11月の問15[3]

適合度検定

標本から求められた度数と理論から仮定される度数が適合するかどうか。

カテゴリー	$A_1$	$A_2$	$\cdots$	$A_k$	合計
観測度数	$f_1$	$f_2$	$\cdots$	$f_k$	$n$
理論度数	$np_1$	$np_2$	$\cdots$	$np_k$	$n$

カイ二乗統計量（K.ピアソンの適合度基準）を計算する

\chi^2=\sum_{i=1}^k \frac{(f_i-np_i)^2}{np_i}

帰無仮説の下で、カイ二乗統計量は自由度は$k-1$の$\chi^2$分布に近似的に従う。$k$はカテゴリーの数。

適合度検定の例

「1等が出る確率10%、2等が出る確率40%、ハズレが出る確率50%」と言われているくじ引きがある。このくじ引きを引いた50人に聞いた結果、1等が出た人数は3人、2等が出た人数は15人、ハズレが出た人数は32人であった。

カテゴリー	1等	2等	ハズレ	合計
観測度数	3	15	32	50
理論度数	50$\times$0.10	50$\times$0.40	50$\times$0.50	100

\chi^2=\frac{(3-50 \times 0.10)^2}{50 \times 0.10}+\frac{(15-50 \times 0.40)^2}{50 \times 0.40}+\frac{(32-50 \times 0.50)^2}{50 \times 0.50}\\
=4.01

カテゴリーの数は3であるから自由度は2である。
自由度2のカイ二乗分布の上側5%点は付表3から5.99であり、有意水準5%において「1等が出る確率10%、2等が出る確率40%、ハズレが出る確率50%」を棄却することはできない。

もっと詳しく

統計学入門p.245

【過去問】
2018年11月の問16
2017年11月の問15

独立性の検定

$n$個の個体が属性$A,B$を持っている。属性Aは$r$個のカテゴリー($A_1,A_2, \cdots, A_r$)に、属性Bは$c$個のカテゴリー($B_1,B_2, \cdots, B_c$)に分割されている。$A_i,B_j$に属する個体の相対度数を$f_{i,j}$とおく。

	$B_1$	$B_2$	$\cdots$	$B_c$	計
$A_1$	$f_{1,1}$	$f_{1,2}$	$\cdots$	$f_{1,c}$	$f_{1,\cdot}$
$A_2$	$f_{2,1}$	$f_{2,2}$	$\cdots$	$f_{2,c}$	$f_{2,\cdot}$
$\vdots$	$\vdots$	$\vdots$		$\vdots$	$\vdots$
$A_r$	$f_{r,1}$	$f_{r,2}$	$\cdots$	$f_{r,c}$	$f_{r,\cdot}$
計	$f_{\cdot,1}$	$f_{\cdot,2}$	$\cdots$	$f_{\cdot,c}$	$n$

期待度数

E_{i,j}=\frac{f_{i,\cdot} f_{\cdot,j}}{n}

観測度数

O_{i,j}=f_{i,j}

カイ二乗統計量

\chi^2=\sum \frac{(O-E)^2}{E}

より、$i,j$それぞれについて$\frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}$を計算し、和をとったものをカイ二乗統計量とする。すなわち

\begin{align}
\chi^2&=\sum_{i=1}^r \sum_{j=1}^c \frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}\\
&=\sum_{i=1}^r \sum_{j=1}^c \frac{(f_{i,j}-\frac{f_{i,\cdot}f_{\cdot,j}}{n})^2}{\frac{f_{i,\cdot}f_{\cdot,j}}{n}}\\
&=\sum_{i=1}^r \sum_{j=1}^c \frac{(n f_{i,j}-f_{i,\cdot}f_{\cdot,j})^2}{n f_{i,\cdot} f_{\cdot,j}}

\end{align}

を計算する。

自由度$(r-1)(c-1)$の$\chi^2$分布を用いて、検定を行う。検定は上側確率で片側検定。

もっと詳しく

統計学入門p.248-250

【過去問】
2018年6月の問15

9. 線形モデル

9-1. 回帰分析

重回帰モデル

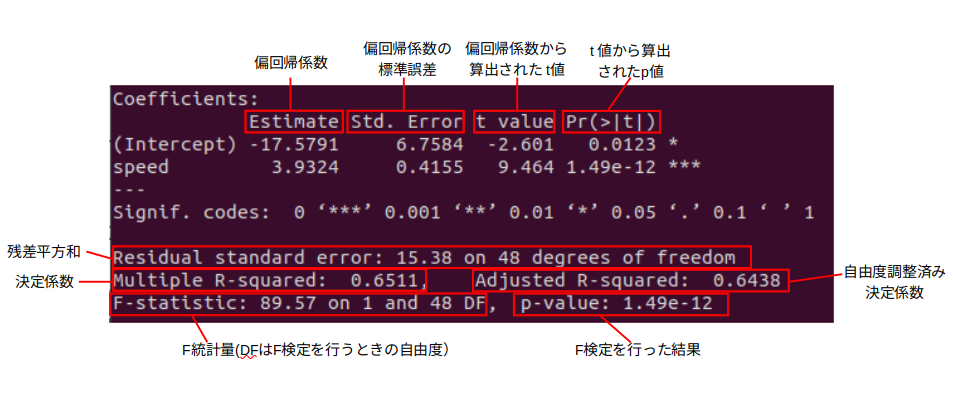
Rの出力結果（carsデータセット、説明変数X:speed、目的変数Y:dist）

標本サイズと自由度の関係

（標本サイズ）=（F統計量の回帰の自由度）+（F統計量の回帰の自由度）+1
上の例ではF-statistic: 89.57 on 1 and 48 DFより標本サイズは1+48+1=50。

標本サイズを$n$, 説明変数の数を$k$とおくと、P値の自由度は$n-k-1$

【過去問】
2019年度6月の問17
2017年度11月の問12

偏回帰係数

$y=\alpha+\beta_1 x_1+\beta_2 x_2$みたいなモデルがあったときの$\alpha, \beta_1, \beta_2$。

偏回帰係数の検定

帰無仮説：偏回帰係数=$\alpha$
対立仮説：偏回帰係数$\neq \alpha$（両側）または（$< \alpha$ または $> \alpha$）（片側）

検定は偏回帰係数を標準誤差で割った値を使って、t統計量を求める。
帰無仮説：$\hat{\beta_i}=\beta_i$
対立仮説：$\hat{\beta_i}\neq \beta_i$（両側）または（$< \beta_i$ または $> \beta_i$）（片側）

$i$番目の偏回帰係数の推定値を$\hat{\beta_i}$、帰無仮説における$i$番目の偏回帰係数の値を$\beta_i$、$\hat{\beta_i}$の標準誤差を$s.e.(\hat{\beta_i})$とおく。

t_i=\frac{\hat{\beta_i}-\beta_i}{s.e.(\hat{\beta_i})}

t分布は自由度$n-k-1$のところを見る。

【過去問】
2018年6月の問14

偏回帰係数の有意性の検定

とくに「帰無仮説：偏回帰係数=0」のときのt統計量(t値)が重要である。なぜならこの帰無仮説が採択されたということは説明変数Xが非説明変数Yを説明できておらず回帰式が不適当となるからである。コンピュータはこのt値を出力する。

有意水準5%の場合、P-値が5%より小さければ帰無仮説を棄却できる（すなわちその偏回帰係数は有意ではないとは言えない）。

もっと詳しく
統計学入門p270,p273

多重共線性

重回帰分析の落とし穴。
線形関係にある（=説明変数間の相関係数が高い）説明変数の組が複数存在すると、解析の精度が低下する。

ダミー変数を用いた回帰

ダミー変数は、クロネッカーのデルタみたいに条件に合えば1になり、そうでなければ0になる。

もっと詳しく

【過去問】
2019年6月の問17
2018年11月の問17[1]

自由度調整済み決定係数

標本サイズと自由度を用いて調整された決定係数。一般的に自由度調整済み決定係数が大きいモデルを選択する。

自由度調整済み決定係数は単回帰モデルでも重回帰モデルでも決定係数と異なる値となる。

Multiple R-squared：決定係数
Adjusted R-squared：自由度調整済み決定係数

【過去問】
2019年6月の問17,18
2018年11月の問17[2]
2018年6月の問14[3]

残差

回帰直線と観測点のy軸方向の距離

【過去問】
2019年11月の問18

残差平方和(residual sum of squares)

残差の2乗の総和。最小二乗法はこれを最小化する。

残差の標準誤差を$\hat{\sigma_u}$、標本サイズを$n$、説明変数の数を$k$とおくと、残差平方和$RSS$は

\hat{\sigma_u}=\frac{RSS}{n-k-1}

の関係がある。（ディープラーニングの2乗和誤差に似ている）

【過去問】
2018年11月の問18[1]

9-2. 実験計画の概念の理解

一元配置分散分析

2つの母集団における母平均の差の検定ではt検定を行った。同様のことを3群（3水準）以上の平均値に拡張して分析するときの手法。各水準の母平均が等しいかどうかをみる。

変動要因	平方和	自由度	平方平均	F値	Pr(>F)
水準間	①	④	⑦	⑨	⑩
残差	②	⑤	⑧
全体	③	⑥

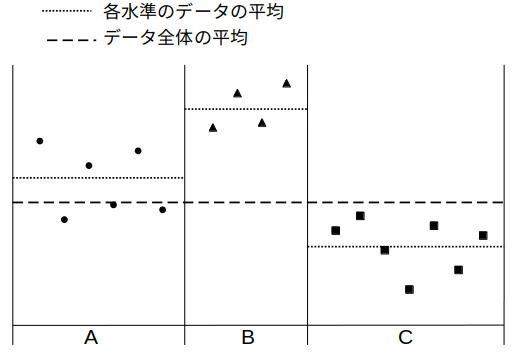
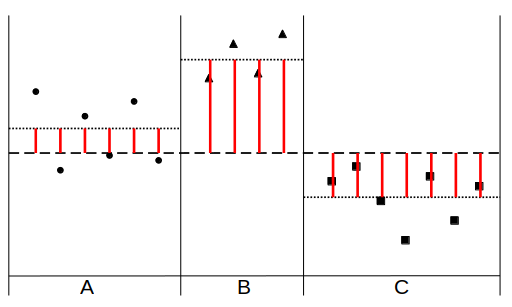
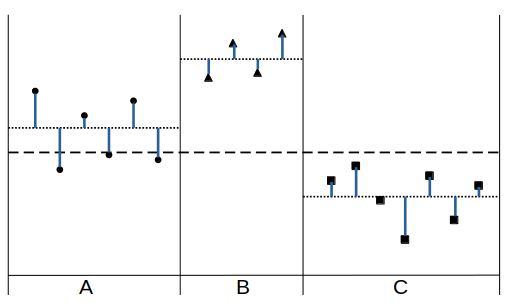
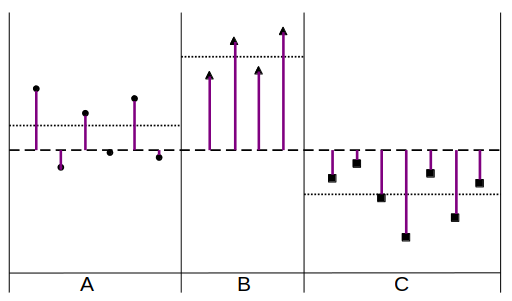
下図のような3水準（A,B,C）に分けられたデータを例とする。

①（全体の平均値と因子の各水準の平均値との差）の平方和

②（各データ点と因子の各水準の平均値との差）の平方和

③（各データ点と全体の平均値との差）の平方和

④（水準間の自由度）＝（水準の数-1）。上図の例では3-1=2。
⑤（残差の自由度）＝（全体の自由度）-（水準間の自由度）。上図の例では16-2=14。先に⑥をもとめておく。
⑥（全体の自由度）＝（データ点の数-1）。上図の例では(6+4+7)-1=16。

⑦（水準間の平均平方）＝①（水準間の平方和）/④（水準間の自由度）
⑧（残差の平均平方）＝　②（残差の平方和）/⑤（残差の自由度）

⑨（F値）＝⑦（水準間の平均平方）/⑧（残差の平均平方）

⑩P値
帰無仮説：全ての水準間で母平均が等しい
対立仮説：すくなくとも1組の水準間で母平均が異なる
有意水準5%のときP値が0.05より小さければ帰無仮説を棄却できる。
P値は（④（水準間の自由度）、⑤（残差の自由度））であるF分布から求める。

ちなみに
③（全体平方和）＝①（水準間平方和）＋②（残差平方和）
標本分散（不偏分散）＝③（全体平方和）÷（標本サイズ-1）

もっと詳しく

【過去問】
2019年11月の問17
2018年6月の問12[2]
2017年11月の問16
2017年6月の問14