この記事の内容
- ベロウソフ・ジャボチンスキー(Belousov-Zhabotinsky, BZ)反応のシミュレーション
- セルオートマトン
- Julia 0.6.2(最後にv1.0向けのコードを追記)
時計反応
BZ反応は時計反応の一種です。通常の化学反応は濃度非平衡から平衡状態へ一直線ですが、時計反応はいくつかの濃度非平衡状態を周期的に繰り返しながら平衡状態に至ります。周期的に増減する化学種が発色するものならば、シャーレ上(平面)では特徴的なパターンとして、撹拌しながらでは周期的な色の変化として、時計反応は観測されます。
BZ反応の実際の動画
同じく時計反応であるBriggs-Rauscher反応を実際にやったことがありますが、色が変わる瞬間は見ていて面白いです。重金属やハロゲン酸塩、過酸化水素を使うので後処理が面倒臭くなかなか気軽にできないのが難点だと思います。
原理
BZ反応中に起こる実際の化学反応は複雑なので、ここでは割愛し、平面に現れる特徴的な円形の波を再現することを目的とします。
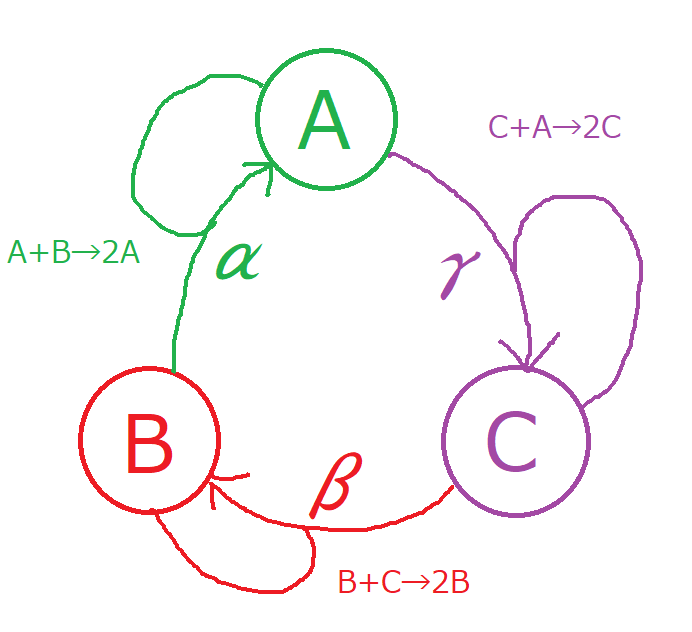
Turnerは3つの化学種A,B,C間で起こる以下の3種の化学反応によってBZ反応の再現ができることを示しました。
A+B \rightarrow 2A (反応パラメータ \alpha)\\
B+C \rightarrow 2B (反応パラメータ \beta)\\
C+A \rightarrow 2C (反応パラメータ \gamma)\\
反応パラメータ$\alpha$,$\beta$,$\gamma$は反応の相対速度を表します。例えば、$\alpha$が増加すると、単位時間に反応するAとBの量は増加し、より多くのAが生成します。
時刻$t$におけるA,B,Cの濃度をそれぞれ$a(t)$,$b(t)$,$c(t)$とおくと、$t$+1における濃度は
a(t+1)=a(t)+\alpha a(t) b(t)-\gamma c(t) a(t)\\
b(t+1)=b(t)+\beta b(t) c(t)-\alpha a(t) b(t)\\
c(t+1)=c(t)+\gamma c(t) a(t)-\beta b(t) c(t)\\
です。
シミュレーションでは、ある1つのセルについて、セル自身の濃度とその周りの計9個のセルの濃度の平均ca,cb,ccを求めて、そのセルの1ステップ後の濃度を計算します。
境界条件:周期境界条件(トーラス型)
計算
Turnerの書いたProcessingコードをJuliaで書き直しました。
α=β=γ=1.0のとき
using Plots
gr(size=(300,300))
h=200
w=200
#α=β=γ=1.0
function update(a,b,c)
tempa.=a
tempb.=b
tempc.=c
for x=1:h,y=1:w
ca=0.0
cb=0.0
cc=0.0
for i=(x-1):(x+1),j=(y-1):(y+1)
if i<1; i=h-i; end
if i>h; i=i-h; end
if j<1; j=w-j; end
if j>w; j=j-w; end
ca+=tempa[i,j]
cb+=tempb[i,j]
cc+=tempc[i,j]
end
ca/=9.0
cb/=9.0
cc/=9.0
a[x,y]=ca+ca*(cb-cc)
b[x,y]=cb+cb*(cc-ca)
c[x,y]=cc+cc*(ca-cb)
end
a=constrain.(a) #broadcast
b=constrain.(b)
c=constrain.(c)
return a,b,c
end
function constrain(d)
if d<0.0
d=0.0
elseif d>1.0
d=1.0
else
d=d
end
return d
end
a=rand(h,w)
b=rand(h,w)
c=rand(h,w)
tempa=zeros(h,w)
tempb=zeros(h,w)
tempc=zeros(h,w)
@time anim = @animate for t in 1:100
heatmap(a,
title="t= $t",
aspect_ratio=:equal)
a,b,c=update(a,b,c)
end
@time gif(anim,"tmp/BZreaction1.gif",fps=5)
47.848051 seconds (386.36 M allocations: 7.531 GiB, 2.81% gc time)
18.724805 seconds (1.38 k allocations: 78.594 KiB)
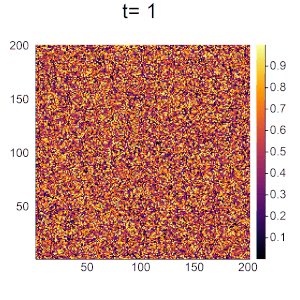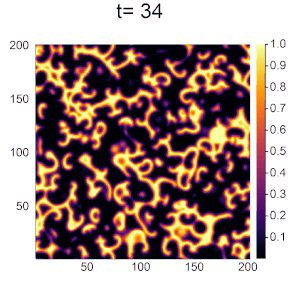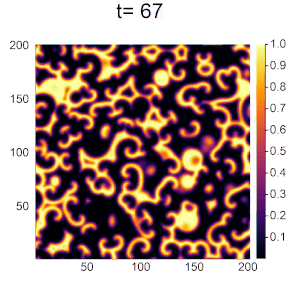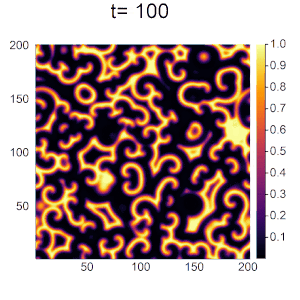
唐草模様のようなパターンができました。BZ反応の形に近づけるために反応パラメータαを調節します。
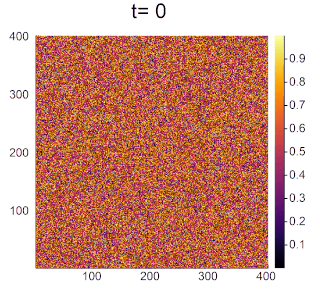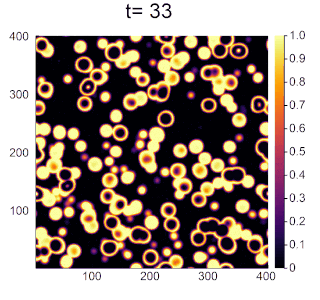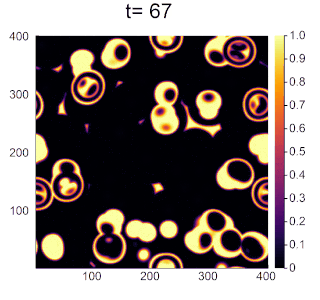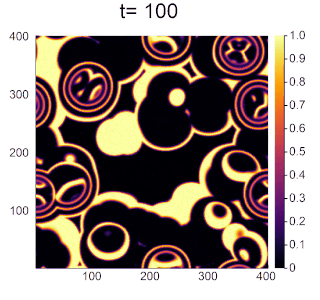
α=1.2,β=γ=1.0のとき
Juliaはギリシャ文字を変数名に使えるのが便利ですね。
using Plots
gr(size=(320,300))
h=400
w=400
α=1.2
β=1.0
γ=1.0
function update(a,b,c)
tempa.=a
tempb.=b
tempc.=c
for x=1:h,y=1:w
ca=0.0
cb=0.0
cc=0.0
for i =(x-1):(x+1),j=(y-1):(y+1)
if i<1; i=h-i; end
if i>h; i=i-h; end
if j<1; j=w-j; end
if j>w; j=j-w; end
ca+=tempa[i,j]
cb+=tempb[i,j]
cc+=tempc[i,j]
end
ca/=9.0
cb/=9.0
cc/=9.0
a[x,y]=ca+ca*(α*cb-γ*cc)
b[x,y]=cb+cb*(β*cc-α*ca)
c[x,y]=cc+cc*(γ*ca-β*cb)
end
a.=constrain.(a) #broadcast
b.=constrain.(b)
c.=constrain.(c)
return a,b,c
end
function constrain(d)
if d<0.0
d=0.0
elseif d>1.0
d=1.0
else
d=d
end
end
a=rand(h,w)
b=rand(h,w)
c=rand(h,w)
tempa=zeros(h,w)
tempb=zeros(h,w)
tempc=zeros(h,w)
@time anim = @animate for t in 0:100
heatmap(a,
title="t= $t",
aspect_ratio=:equal
)
a,b,c=update(a,b,c)
end
@time gif(anim,"tmp/BZreaction2.gif",fps=5)
115.282088 seconds (1.59 G allocations: 29.718 GiB, 3.38% gc time)
18.357824 seconds (1.38 k allocations: 78.563 KiB)
実際のBZ反応のような円形波が見られるようになりました。
つまづいたところ
- 1ステップ前の濃度行列(temp)を使わないと、変更後の濃度を参照してしまい結果がおかしくなる(空間異方性が混入し、原点方向に流れる進行波になる、それはそれで非同期型セルオートマトンとして面白い現象だ)。濃度を一度temp行列に保存し、それを参照して濃度を変更するようにしないといけない。
- 計算後、濃度範囲を0.0-1.0内に収める処理をしないと発散する。
- 系のサイズが小さすぎると発散する(α=1.2, β=γ=1.0のとき100×100ではt=140くらいで発散)
- 行列ではA=Bはポインタ渡し、A.=Bで値渡し。
参考文献
- A. Turner, "A simple model of the Belousov-Zhabotinsky reaction from first principles", 2009.
http://discovery.ucl.ac.uk/17241/1/17241.pdf - BZ reaction by Alasdair Turner OpenProcessing https://www.openprocessing.org/sketch/1263#
20180613追記
頂いた感想をもとにコードを修正しました。
変更点
- update関数の仮引数をなくし、グローバル変数a,b,cをそのまま処理する
- 自作関数constrainを、備え付けのBase.Math.clampに変更
計算
using Plots
gr(size=(320,300))
h=400
w=400
α=1.2
β=1.0
γ=1.0
a=rand(h,w)
b=rand(h,w)
c=rand(h,w)
tempa=zeros(h,w)
tempb=zeros(h,w)
tempc=zeros(h,w)
function update()
tempa.=a
tempb.=b
tempc.=c
for x=1:h,y=1:w
ca=0.0
cb=0.0
cc=0.0
for i =(x-1):(x+1),j=(y-1):(y+1)
if i<1; i=h-i; end
if i>h; i=i-h; end
if j<1; j=w-j; end
if j>w; j=j-w; end
ca+=tempa[i,j]
cb+=tempb[i,j]
cc+=tempc[i,j]
end
ca/=9.0
cb/=9.0
cc/=9.0
a[x,y]=ca+ca*(α*cb-γ*cc)
b[x,y]=cb+cb*(β*cc-α*ca)
c[x,y]=cc+cc*(γ*ca-β*cb)
end
a.=clamp.(a,0.0,1.0) #broadcast
b.=clamp.(b,0.0,1.0)
c.=clamp.(c,0.0,1.0)
end
@time anim = @animate for t in 0:100
heatmap(a,
title="t= $t",
aspect_ratio=:equal
)
update()
end
@time gif(anim,"tmp/BZreaction3.gif",fps=5)
119.262235 seconds (1.59 G allocations: 29.716 GiB, 3.33% gc time)
19.932928 seconds (1.42 k allocations: 80.328 KiB)
(動画は月ごとのアップロード制限があるため省略しますが、うえで述べたα=1.2,β=γ=1.0のときのコードと同様の結果となります。)
v1.0対応&高速化バージョン
#BZ-reaction simulation
#reference=>http://discovery.ucl.ac.uk/17241/1/17241.pdf
#julia v1.0
using Plots
gr(size=(320,300))
#初期状態を固定するために追加
using Random
Random.seed!(1234)
module BZReact
struct Param
#系のサイズ
h::Int64
w::Int64
#反応速度
α::Float64
β::Float64
γ::Float64
end
mutable struct Variables
#濃度
a::Array{Float64,2}
b::Array{Float64,2}
c::Array{Float64,2}
#一世代前の濃度
tempa::Array{Float64,2}
tempb::Array{Float64,2}
tempc::Array{Float64,2}
end
end
#using .BZReact
h=400
w=400
α=1.2
β=1.0
γ=1.0
param1=BZReact.Param(h,w,α,β,γ)
a=rand(h,w)
b=rand(h,w)
c=rand(h,w)
tempa=zeros(h,w)
tempb=zeros(h,w)
tempc=zeros(h,w)
var1=BZReact.Variables(a,b,c,tempa,tempb,tempc)
function update(param,var,t)
var.tempa.=var.a
var.tempb.=var.b
var.tempc.=var.c
for x=1:param.h,y=1:param.w
ca=0.0
cb=0.0
cc=0.0
for i =(x-1):(x+1),j=(y-1):(y+1)
if i<1; i=param.h-i; end
if i>param.h; i=i-param.h; end
if j<1; j=param.w-j; end
if j>param.w; j=j-param.w; end
ca+=var.tempa[i,j]
cb+=var.tempb[i,j]
cc+=var.tempc[i,j]
end
ca/=9.0
cb/=9.0
cc/=9.0
var.a[x,y]=ca+ca*(param.α*cb-param.γ*cc)
var.b[x,y]=cb+cb*(param.β*cc-param.α*ca)
var.c[x,y]=cc+cc*(param.γ*ca-param.β*cb)
end
var.a.=clamp.(var.a,0.0,1.0) #broadcast
var.b.=clamp.(var.b,0.0,1.0)
var.c.=clamp.(var.c,0.0,1.0)
heatmap(var.a,
title="t= $t",
aspect_ratio=:equal
)
end
@time anim = @animate for t in 0:100
update(param1,var1,t)
end
@time gif(anim,"tmp/BZreaction4.gif",fps=5)
6.756628 seconds (84.47 M allocations: 2.543 GiB, 5.41% gc time)
0.848957 seconds (640 allocations: 36.531 KiB)
計算時間120sec→10sec以下に!