PythonでABC259F

Upsolveしたので、理解を強固にするために解説記事を書きました。

問題へのリンク

提出コード

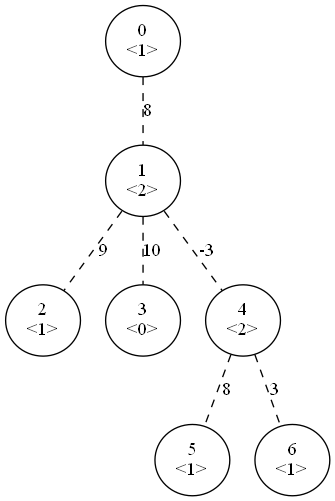
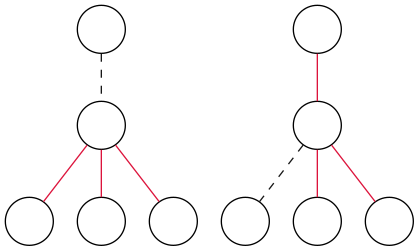
問題のイメージ

$N$個の頂点と$N-1$本の辺からなる木があります。0本以上の辺を選んだ時重みの最大値はいくつでしょうか。ただし、各頂点$i$において選んだ辺の次数が$d_i$を超えてはいけません。

辺を蛍光灯に見立てて、それぞれの辺についてON/OFFを決めていくことを考えます。$d_i$のルールを守りながら、ON辺の重みの総和が最大になるようにしていきます。

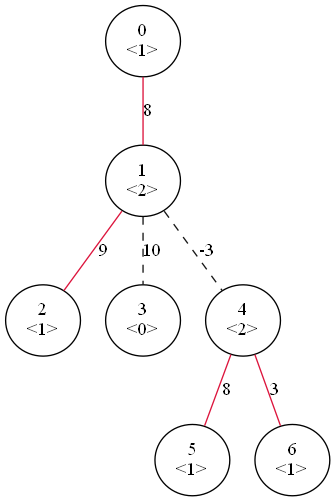
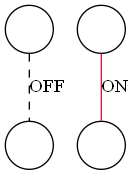
以下では、OFF辺を黒色の点線、ON辺を赤色の実線で示します。

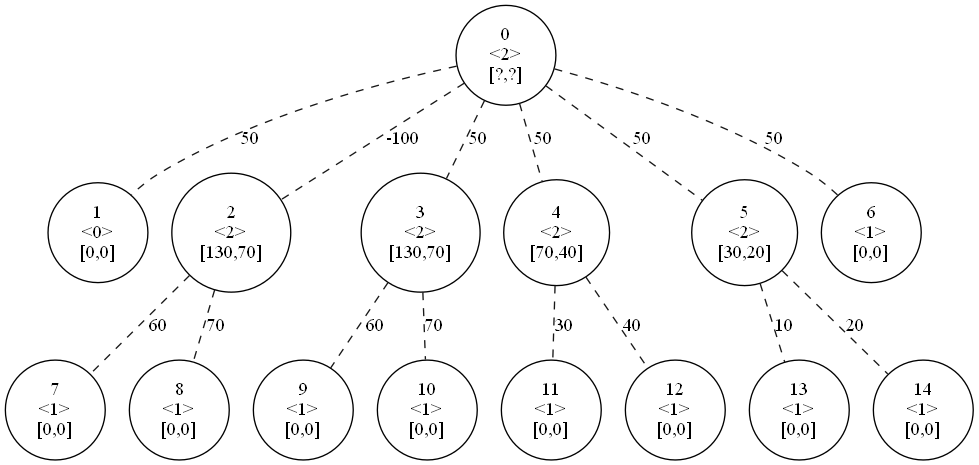
サンプル１をもとに、この問題でやろうとしていることをイメージしてみます。ここでは、頂点を0-indexに変えてあります。<>内の数字は$d_i$です。

最初、すべての辺はOFFです。

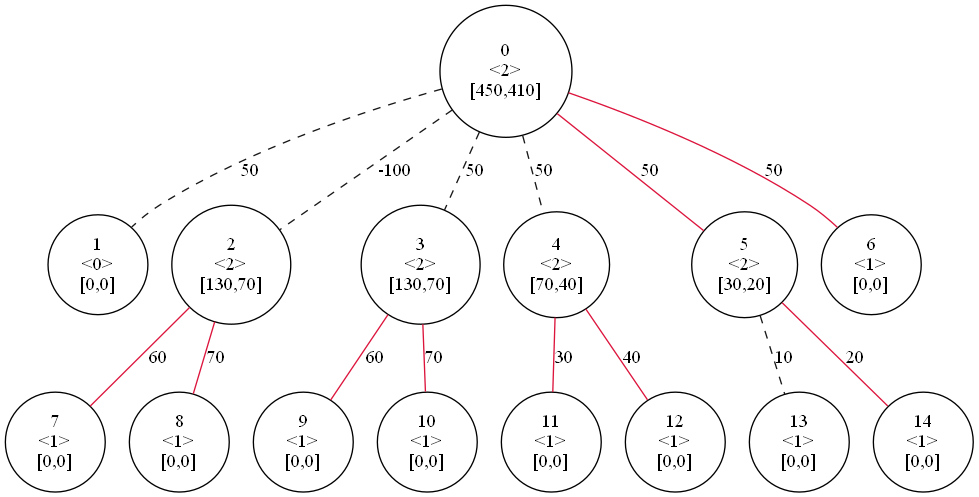
このときの正答は↓になります。

ON辺は$0$本でもよいし、$N-1$本すべてでもよいです。ON辺のみで木をなしている必要はなく、途中で途切れていてもよいです。

それでは、最適解を導き出すアルゴリズムはどのようになるでしょうか？

考察

部分木から考える

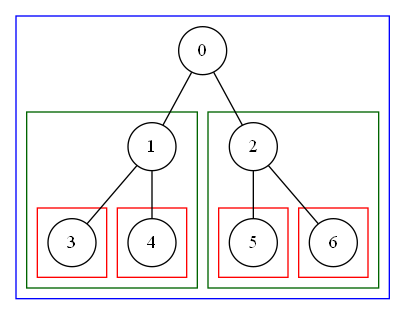
全体の最適解を一発で決めるのが難しいときは、小さなパーツに分けて考えてから徐々に大きくしていくのが定石です。ということで、部分木について思いを馳せます。

下図でいうと青→緑→赤のように、木の部分木、その部分木のそのまた部分木と、どんどん細かくしていくと、最終的に葉のところでは頂点1つだけの部分木になります。この最小単位の部分木における重み総和の最大値は必ず0です（辺を持たないのため）。これで最も小さなパーツの値が定ままりました。これを足掛かりにして子から親へとさかのぼっていきましょう。

2種類の状態

「子頂点の部分木」から「親頂点の部分木」への遷移の仕方を考えます。

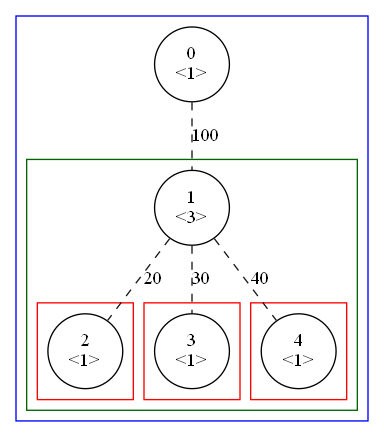
例として、以下のような木の重み総和の最大値を求めてみます。

さきほどの方針通り、子から親への方向へ「重み総和の最大値」を決めていきます。
赤色部分の重み総和の最大値はそれぞれ0です。
緑色エリア（頂点1以下の部分木）の重み総和の最大値を考えます、$d_i$の許すかぎり貪欲に辺をOFFからONに変えていくと、3本ある辺すべてをONにできて、最大値は20+30+40=90です。
次に、青色エリア（木全体）を見てみます。頂点1にはすでにON辺が3本つながっているので0と1をつなぐ辺を選ぶことができません。しかし、あきらかに重み100である辺をONにしたほうが重み総和の最大値は大きくなります。実際のこの木の最適解は30+40+100=170です。

このケースが示唆することは、「頂点$v$以下の部分木における、$d_v$本の辺をすべて使いきった時の重み総和の最大値」だけを保持していては「親頂点の部分木における重み総和の最大値」を求めるには不十分だということです。辺をONにできる権利を1本残しておいて、頂点$v$とその親を結ぶ辺をONにできるようにしておいたときのほうが良い場合もあります。

左：親への辺を残しておかない場合、右：親への辺をONにする権利を残しておき、かつ、その権利を使って親への辺をONにした場合

木DP

ここまでの考察から、各頂点以下の部分木において2つの状態を保持しながら、子から親へと遷移させていきます。具体的には、以下のような2つの状態を保持してDPをしていきます。

\begin{align}
dp[v][0] &= 頂点v以下の部分木について、vに接続する辺をd_v本以下ONにしたときの重み総和の最大値\\

dp[v][1] &= 頂点v以下の部分木について、vに接続する辺をd_v-1本以下ONにしたときの重み総和の最大値
\end{align}

$dp[v][0]$が親への辺を残しておかない状態、$dp[v][1]$が1本節約して親への辺をONにする余裕を残しておいた状態に対応します。この2つの状態の大小関係は常に$dp[v][0] \geq dp[v][1]$になります。

特殊な例として、$d_v=0$のとき、辺を1本残しておくということは不可能ですから $dp[v][1]=-\infty$ としておきます。

辺の選び方

最後に考えるのは、複数の辺が存在する場合に、どのように優先度を付けて辺をONにすればよいのかということです。以下のようなケースを考えます。

15
2 0 2 2 2 2 1 1 1 1 1 1 1 1 1
1 2 50
1 3 -100
1 4 50
1 5 50
1 6 50
1 7 50
3 8 60
3 9 70
4 10 70
4 11 60
5 12 30
5 13 40
6 14 10
6 15 20

頂点0を根として、この木は深さ0,深さ1,深さ2の階層に分けられます。深さ1の頂点1,2,3,4,5,6のdp[v]の計算まではすでに終わっているとして、頂点0とその子頂点$u_i=1,2,3,4,5,6$をつなぐ重み$w_i$の辺を選んでONにしていくプロセスを詳しく見てみます。

はじめ、辺6本はすべてOFFです。
辺(0,1)はONにできません。頂点1が$d_v=0$であるため。
辺(0,2)の重みは負なので、この辺をONにすると損します。
辺(0,3)をONにすると、かわりに辺(3,9)をOFFにしなければいけません。60を捨てて50を拾うため10だけ損します。
辺(0,4)をONにすると、かわりに辺(4,11)をOFFにしなければいけません。30を捨てて50を拾うため20得します。
辺(0,5)をONにすると、かわりに辺(4,11)をOFFにしなければいけません。10を捨てて50を拾うため40得します。
辺(0,6)をONにすると、単純に50得します。

これらの観察から、辺をOFFからONに変えたときは$dp[u_i][0]$を捨てて$dp[u_i][1]+w_i$を拾うことがわかります。
辺をONにしたときのお得度を

\Delta_i=-dp[u_i][0]+(dp[u_i][1]+w_i)

と定義するとよさそうです。このように定義すると、辺をONにすることができないときやONにすると損するときは$\Delta_i<0$になります。

$u_i$	1	2	3	4	5	6
$dp[u_i][0]$	0	130	130	70	30	0
$dp[u_i][1]$	$-\infty$	70	70	40	20	0
$w_i$	0	-100	50	50	50	50
$\Delta_i=-dp[u_i][0]+(dp[u_i][1]+w_i)$	$-\infty$	-160	-10	20	40	50

dp[v][0]を得るには、お得度$\Delta_i$を降順ソートして、その順番で、$d_v$本以下かつ$\Delta_i>0$であるかぎり辺をONにしていくのがよいです。今のケースだとお得度は[6,5,4,3,2,1]の順番になり、$d_0=2$であることから辺(0,6),(0,5)をONにするのが最適です。もし$d_0=4$であるときは、辺(0,6),(0,5),(0,4)をONにするのが最適です（辺(0,3)はお得度が負のためONにしません）。
同様に、dp[v][1]を得るには、お得度$\Delta_i$を降順ソートして、その順番で、 $d_v$-1 本以下 かつ$\Delta_i>0$であるかぎり辺をONにしていくのがよいです。

最終的にdp[0][0]が答えとなります。今ケースの答えは450です。

実装

アルゴリズムを実現するには、まず、葉から根へ向かう順番で頂点にアクセスする必要があります。そうしないと、ある頂点にアクセスしたときにその子頂点のdpの値が未定である事態が発生します。2つのやり方があります。

1. 幅優先探索を行って「行きがけ順」をメモし、その逆順に頂点へアクセスする（＝深さが大きい頂点から順に決めていく）。
2. 深さ優先探索を用いて木の末端から決めていく。

今回は1を使います。

実装ソースコードは下記です。わかりやすさ重視のため記述が冗長になっていることがあります。

from collections import deque
N = int(input())
d = list(map(int, input().split()))
graph = [[] for _ in range(N)]

for _ in range(N-1):
    a, b, w = map(int, input().split())
    a, b = a-1, b-1
    graph[a].append((b, w))
    graph[b].append((a, w))

#頂点0を根とする
start = 0

#訪問したかどうか
is_visited = [False]*N
is_visited[start] = True

#訪問した順
order_visited = []
order_visited.append(start)

#親頂点をメモしておく
parent_node = [-1]*N

#幅優先探索で行きがけ順を記録する
q = deque()
q.append(start)

while q:
    v = q.popleft()
    for u, _ in graph[v]:
        if not is_visited[u]:
            is_visited[u] = True
            order_visited.append(u)
            parent_node[u] = v
            q.append(u)

#木DP
dp = [[0, 0] for _ in range(N)]
INF = 10**18

for v in reversed(order_visited):
    
    #子頂点それぞれについてお得度Deltaを計算する
    chile_info = []

    for u, w in graph[v]:
        if u == parent_node[v]:
            continue

        chile_info.append([u, w, dp[u][1]+w-dp[u][0]])

    #お得度で降順ソート
    chile_info.sort(reverse=True, key=lambda x: x[2])

    #dp[v][0]を計算（親への辺を残しておかない場合）
    for i, (u, w, delta) in enumerate(chile_info):
        if i+1 <= d[v] and delta > 0:
            dp[v][0] += dp[u][1]+w
        else:
            dp[v][0] += dp[u][0]

    #dp[v][1]を計算（親への辺を残しておく場合）
    for i, (u, w, delta) in enumerate(chile_info):
        if i+1 < d[v] and delta > 0:
            dp[v][1] += dp[u][1]+w
        else:
            dp[v][1] += dp[u][0]

    if d[v] == 0:
        dp[v][1] = -INF

print(dp[0][0])

参考文献