Pythonで粘菌ネットワーク

概説

粘菌数理モデルが最短経路を求める様子をgif動画にしてみた

粘菌ネットワークとは

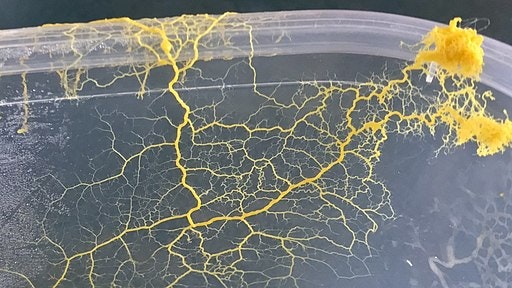
粘菌は餌が近くにある時、自身の体で栄養を運ぶ管のネットワークを構築します。そのネットワークはしばしば餌場間の輸送効率の良いネットワークを構築することが知られています。そんな粘菌のふるまいにヒントを得て中垣俊之らによってつくられたのが粘菌数理モデルです。中垣らはこのような粘菌に関する研究によって2008年と2010年に栄えあるイグノーベル賞を受賞しています。

Norty Edwards, CC BY-SA 3.0, via Wikimedia Commons

ゆる生態学ラジオ【イグノーベル賞2冠】粘菌迷路の研究者が来たぞ！【粘菌1】#93

粘菌と鉄道会社。より良い路線図を作れるのはどっち？【粘菌2】#94

　「粘菌が迷路を解く」というワードはそのインパクトもあってか広く知られていますが、背景にある数理モデルを解説した資料はあまり多くありません。そこで本記事では数理モデルの解説とポピュラーな言語であるPythonを用いた可視化を試みます。

粘菌数理モデル

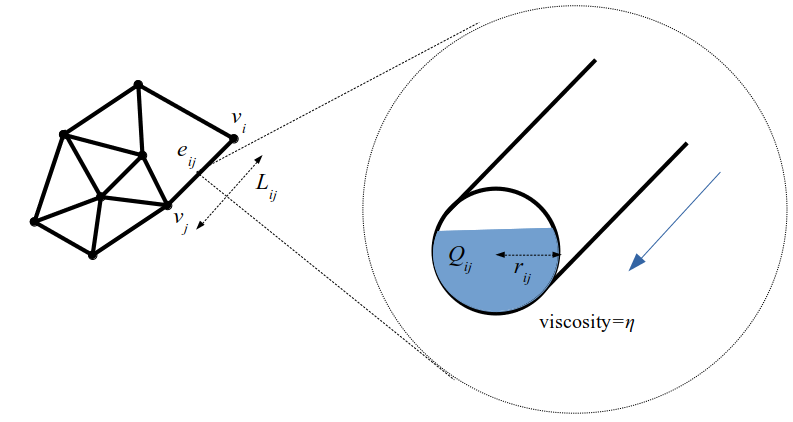
粘菌ネットワークでは、粘菌の体を$N$個の 頂点（ノード） とそれどうしをつなぐ 栄養管(エッジ) から構成されるグラフとみなします。ある頂点が 栄養の供給源（餌,Source） 上にあり、他のある頂点を 栄養を消費する場所(Sink) とします。餌場で供給された栄養は栄養管の中を流れて消費場所まで流れます。時間発展の中で、流量の少ない栄養管はその太さを維持していてもエネルギーの無駄なので細くしていき、逆に流量の多い栄養管はもっと太くしてより効率的に栄養が運べるように自らを調節します。その結果、粘菌ネットワークはより輸送効率の良い流れとなります。

まず、粘菌ネットワークの頂点とそれらをつなぐ栄養管を以下のようにグラフとして表記します。

記号	意味
$v_i$	$i$番目の頂点($i$=1,2,3,$\cdots$,$N$)
$e_{ij}$	$i$番目の頂点と$j$番目の頂点をつなぐ栄養管

$e_{ij}$の中を$v_i$から$v_j$方向に流れる 単位時間当たりの餌（栄養）の流量$Q_{ij}$ は粘性のある流体の流れ（ハーゲン・ポアズイユ流れ）を仮定すると以下のように書き表されます。

Q_{ij}=\frac{\pi r_{ij}^4}{8\eta L_{ij}} (p_i-p_j)\tag{1}

物理量の意味は以下の表を参照してください。

物理量	意味
$\pi$	円周率
$r_{ij}$	栄養管$e_{ij}$の半径（壁の厚さは考慮しない）
$\eta$	栄養管を流れる流体の粘性率
$p_i$	$i$番目のノードでの圧力
$p_j$	$j$番目のノードでの圧力
$L_{ij}$	$e_{ij}$の経路長

全ての頂点は栄養管の末端または栄養管どうしのつなぎ目でしかなく、頂点自体は体積ゼロであり、頂点に栄養流体は滞積しません。

ここで、

D_{ij}=\frac{\pi r_{ij}^4}{8\eta}\tag{2}

となる変数$D_{ij}$を定義すると式1は以下のように書き換えられます。

Q_{ij}=\frac{D_{ij}}{L_{ij}} (p_i-p_j)\tag{3}

$D$は 単位長さ当たりの流れやすさ(Conductivity) を意味します。栄養管の中を流れる栄養流体の粘性率$\eta$が栄養管によらず一定であると仮定すると、$D$の値は栄養管がどれくらい太いかということを示します。$D$が大きければその栄養管は太く、小さければ細いです。$D$は時間がたつにつれて変化します。その変化量は以下の式に基づいて導出されます。

\frac{dD_{ij}}{dt}=f(|Q_{ij}|)-D_{ij}\tag{4}

$f(|Q|)$は 流量強化関数 といい、栄養管を流れる栄養の流量に応じてどれくらい流れやすさが変化するかを意味し、$D_{ij}$は栄養管が細くなる効果（栄養管の維持コスト）を意味します。
$f(|Q|)$の中身を

f(|Q|)=\frac{|Q|^\gamma}{1+|Q|^\gamma}\tag{5}

とおきます。式4,5から栄養の流量が多くなるほどその栄養管は太くなりさらに流れやすさがアップし、流量が少なく使われていない栄養管は自ら細くなっていき栄養がより流れにくくなることがわかります。

栄養管の長さや流れやすさは流れの向きによらないものとします。式3より$Q$は$i$,$j$を入れ替えると符号は反転します。

\displaylines{
L_{ij}=L_{ji}　\\
D_{ij}=D_{ji}　\\
Q_{ij}=-Q_{ji}\tag{6}
}

頂点の中から餌場所となる頂点を選択します。この説明では$v_1$を餌ノード(Source)、$v_2$をもうひとつの餌ノード(Sink)とします。$v_1$では単位時間あたり$I_0$の栄養が供給されます。$v_2$では単位時間当たり$I_0$の栄養が消費されます（＝マイナスの栄養が供給されるともいえる）。この2つ以外からの栄養の出入りはありません。キルヒホッフの法則（各ノードにおいて流入の総和と流出の総和は等しいという法則、電磁気学でおなじみ）を考えると、

\sum_j Q_{ij} = \left\{
\begin{array}
 +I_0 & (i=1) \\
-I_0 & (i=2) \\
 0 & (i\neq1,2)
\end{array}
\right.

となります。この式は「ある1つの頂点を選んで、単位時間当たりに他の頂点から流入した分と他の頂点へ流出した分の合計をとったとき、その値は、その頂点が$v_1$なら$I_0$、$v_2$なら$-I_0$、それ以外の頂点なら0になっている」ということを言っています。

アルゴリズム

数理モデルのルールを一通り学んだところで、次は実際にどのようなステップを踏んで計算を進めていくかについて簡単なグラフを使いながら説明します。

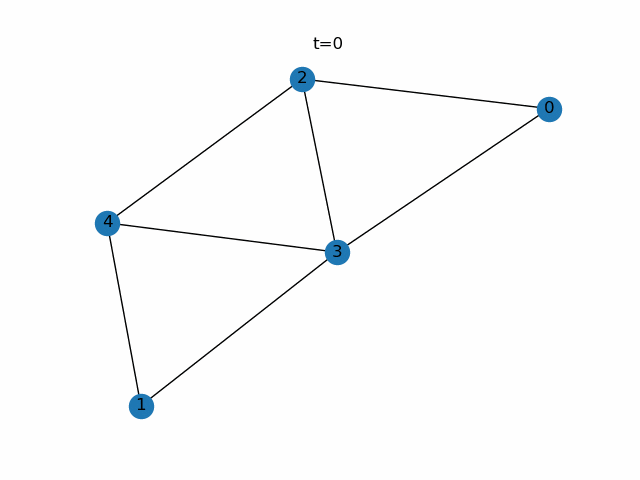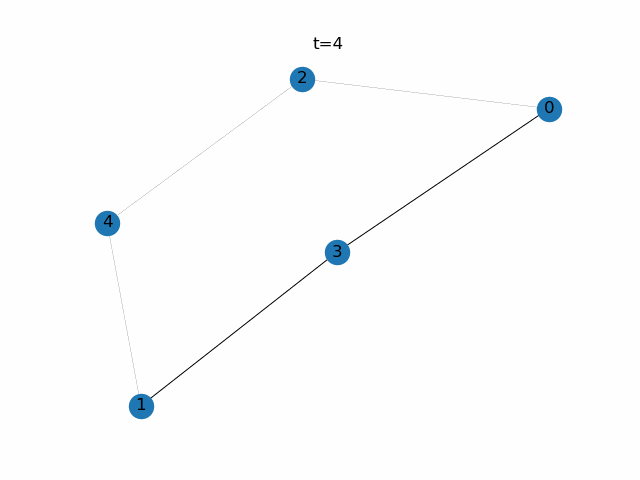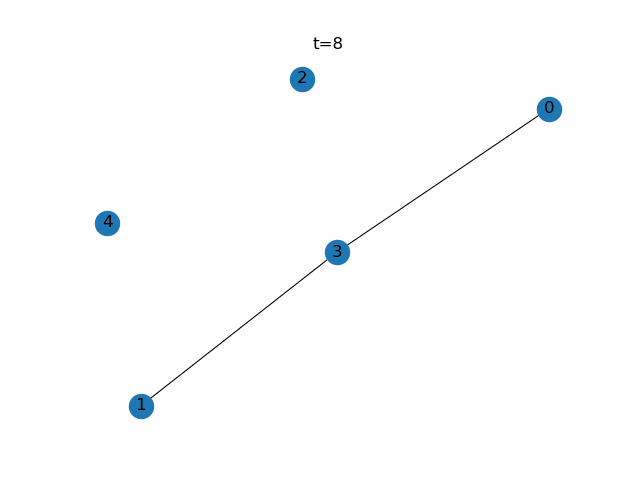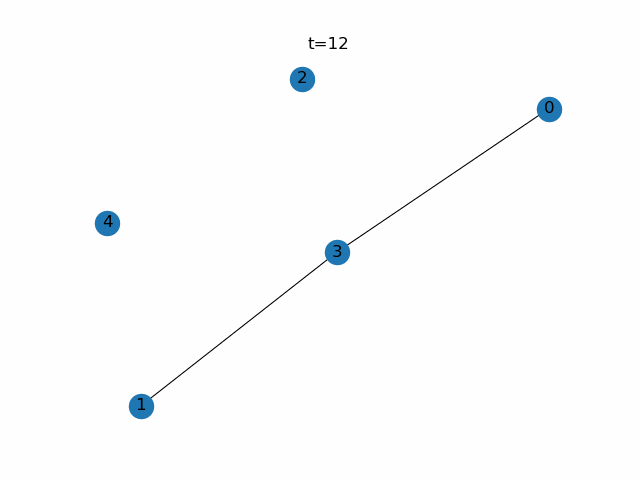
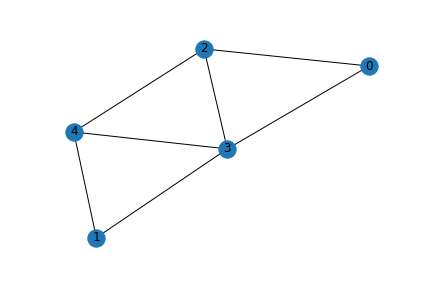
step0.使うグラフ

図のような5個のノードからなる無向グラフについて考えます。

import networkx as nx
import matplotlib.pyplot as plt
import numpy as np

G=nx.Graph()
G.add_nodes_from([0,1,2,3,4])
G.add_edges_from([(0,2),(0,3),(2,3),(2,4),(1,4),(1,3),(3,4)])
pos = nx.spring_layout(G)
nx.draw_networkx(G,pos)
plt.axis('off')
plt.show()

このグラフは隣接行列を用いて以下のように書けます。隣接行列は頂点どうしがつながっているかどうかを示します。つながっていれば1、つながっていなければ0です。隣接行列の一番上、左から3番目（0行2列目、Pythonではインデックスが0から始まることに注意してください）は「1」ですから頂点0と頂点2はつながっています。

\left(
\begin{matrix}
0&0&1&1&0 \\
0&0&0&1&1 \\
1&0&0&1&1 \\
1&1&1&0&1 \\
0&1&1&1&0
\end{matrix}
\right)\tag{8}

nbr_mtx=nx.to_numpy_matrix(G)

step.1 使う変数

各エッジの流れやすさ、長さ、各ノードの圧力、各エッジの流量をそれぞれ以下のように定義します。

\boldsymbol{D}=\left(
\begin{matrix}
0&0&D_{02}&D_{03}&0 \\
0&0&0&D_{13}&D_{14} \\
D_{20}&0&0&D_{23}&D_{24} \\
D_{30}&D_{31}&D_{32}&0&D_{34} \\
0&D_{41}&D_{42}&D_{43}&0
\end{matrix}
\right), \\
\quad\\
\boldsymbol{L}=\left(
\begin{matrix}
0&0&L_{02}&L_{03}&0 \\
0&0&0&L_{13}&L_{14} \\
L_{20}&0&0&L_{23}&L_{24} \\
L_{30}&L_{31}&L_{32}&0&L_{34} \\
0&L_{41}&L_{42}&L_{43}&0
\end{matrix}
\right), \\
\quad\\
\boldsymbol{p}=\left(
\begin{matrix}
p_0\\
p_1\\
p_2\\
p_3\\
p_4\\
\end{matrix}
\right), \\
\boldsymbol{Q}=\frac{\boldsymbol{D}}{\boldsymbol{L}}(\boldsymbol{p}^T-\boldsymbol{p})\tag{9}

step.2 一次連立方程式を立てて解き、圧力を求める

さて、ノード0が餌ノード($+I_0$)、ノード1をもうひとつの餌ノード($-I_0$)とおくと、式7より

\begin{align}
Q_{02}+Q_{03}&=I_0\\
Q_{13}+Q_{14}&=-I_0\\
Q_{20}+Q_{23}+Q_{24}&=0\\
Q_{30}+Q_{31}+Q_{32}+Q_{34}&=0\\
Q_{41}+Q_{42}+Q_{43}&=0
\end{align}\tag{10}

が成立します。式3からこの一次連立方程式は以下の行列形式に変換できます。

\left(
\begin{matrix}
\frac{D_{02}}{L_{02}}+\frac{D_{03}}{L_{03}}&
0&
-\frac{D_{02}}{L_{02}}&
-\frac{D_{03}}{L_{03}} &
0\\
0&
\frac{D_{13}}{L_{13}}+\frac{D_{14}}{L_{14}}&
0&
-\frac{D_{13}}{L_{13}}&
-\frac{D_{14}}{L_{14}} \\
-\frac{D_{20}}{L_{20}}&
0&
\frac{D_{20}}{L_{20}}+\frac{D_{23}}{L_{23}}+\frac{D_{24}}{L_{24}}&
-\frac{D_{23}}{L_{23}}&
-\frac{D_{24}}{L_{24}}\\
-\frac{D_{30}}{L_{30}}&
-\frac{D_{31}}{L_{31}}&
-\frac{D_{32}}{L_{32}}&
\frac{D_{30}}{L_{30}}+\frac{D_{31}}{L_{31}}+\frac{D_{32}}{L_{32}}+\frac{D_{34}}{L_{34}}&
-\frac{D_{34}}{L_{34}}\\
0&
-\frac{D_{41}}{L_{41}} &
-\frac{D_{42}}{L_{42}}&
-\frac{D_{43}}{L_{43}}&
\frac{D_{41}}{L_{41}}+\frac{D_{42}}{L_{42}}+\frac{D_{43}}{L_{43}}
\end{matrix}
\right)
\left(
\begin{matrix}
p_0\\p_1\\p_2\\p_3\\p_4
\end{matrix}
\right)
=
\left(
\begin{matrix}
I_0\\-I_0\\0\\0\\0
\end{matrix}
\right)\tag{11}

左辺の大きな行列（以後行列$\boldsymbol{A}$と呼びます）が逆行列を持つ場合連立方程式は解を持ち、方程式を解けば$\boldsymbol{p}$が求まります。行列$\boldsymbol{A}$の各成分をよく見ると以下のような法則が成り立っていることがわかります。この法則が分かれば、自分で行列$\boldsymbol{A}$を作ることができます。

\displaylines{
（対角成分）\sum_{j=neighbors}\frac{D_{ij}}{L_{ij}} \\
（隣接あり）-\frac{D_{ij}}{L_{ij}} \\
（隣接なし）0
}

step.3 圧力から次世代の流れやすさを求める

$\boldsymbol{p}$が求まれば$\boldsymbol{Q}$を求めることができ、式4,5から次世代の$\boldsymbol{D}$が計算できます。

\begin{align}
D(t+dt)&=D(t)+dD\\
&=D(t)+(f(|Q(t)|)-D(t))dt\tag{12}
\end{align}

step.4 step.2と3を繰り返す

次世代の$\boldsymbol{D}$がわかれば次世代の$\boldsymbol{p}$が求まります。次世代の$\boldsymbol{p}$がわかれば次々世代の$\boldsymbol{D}$がわかります。あとはその繰り返しです。

計算

• Anaconda+Jupyter notebookで実行
• Python3.6.8
• matplotlib 3.0.3
• numpy 1.16.3
• networkx 2.3

$D$の非ゼロ要素の初期値は全て1.0とします。今回各エッジの長さは常に1とします。

import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import PillowWriter, FuncAnimation

G=nx.Graph()
G.add_nodes_from([0,1,2,3,4])
G.add_edges_from([(0,2),(0,3),(2,3),(2,4),(1,4),(1,3),(3,4)])
pos = nx.spring_layout(G)

#変数宣言
nt=13
#今回はdt=1とする
nnodes=nx.number_of_nodes(G)
edge_list=list(G.edges)
nbr_mtx=nx.to_numpy_matrix(G)

conductivity=np.zeros((nt,nnodes,nnodes)) #D
length=np.zeros((nnodes,nnodes)) #L
pressure=np.zeros((nt,nnodes)) #p
flux=np.zeros(nnodes) #Q

#初期値と定数の設定
conductivity[0]=nbr_mtx #各エッジの流れやすさは最初1.0
length=nbr_mtx #今回は各エッジの長さは1.0とする
I0=2.0
flux[0]=I0
flux[1]=-I0
gamma=1.8

#ゼロ除算が発生しないように非ゼロ要素のみで割り算を行う
def divide_non_zero_element(D,L,num_nodes,list_edges):
    X=np.zeros((num_nodes,num_nodes))
    for i,j in list_edges:
        X[i,j]=D[i,j]/L[i,j]
        X[j,i]=D[j,i]/L[j,i]
    return X

#f(Q) for dD/dt 
def f(x):
    powered=x**gamma
    return powered/(powered+1)

#Dの時間変化量を求める
def dD(D,L,p,num_nodes,list_edges):
    X=divide_non_zero_element(D,L,num_nodes,list_edges)
    Q=np.multiply(X,np.expand_dims(p,axis=1)-p)
    ans=f(np.abs(Q))
    return ans

#一次連立方程式を解きpを求める
def deduce_p(D,L,B,num_nodes,list_edges):
    Y=divide_non_zero_element(D,L,num_nodes,list_edges)    
    A=np.diag(np.sum(Y,axis=1))-Y
    p=np.linalg.solve(A,B)
    return p

#pの初期値を求める
pressure[0]=deduce_p(conductivity[0],length,flux,nnodes,edge_list)

#繰り返し計算する
for t in range(0,nt-1):
    conductivity[t+1]=dD(conductivity[t],length,pressure[t],nnodes,edge_list)
    pressure[t+1]=deduce_p(conductivity[t+1],length,flux,nnodes,edge_list)

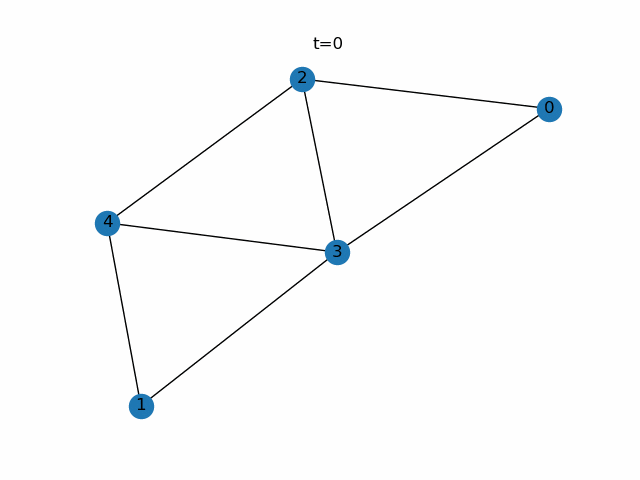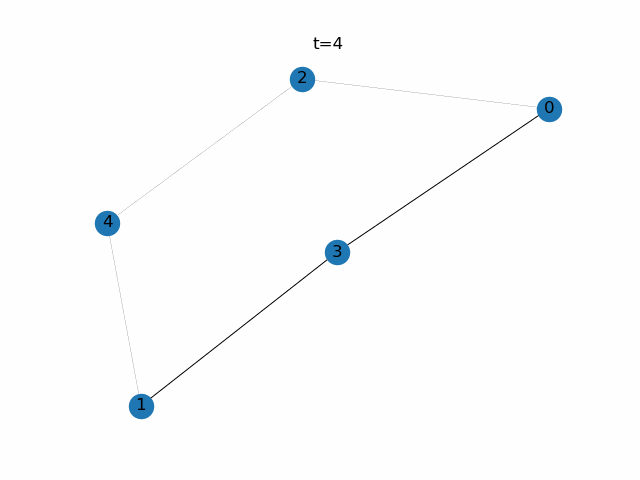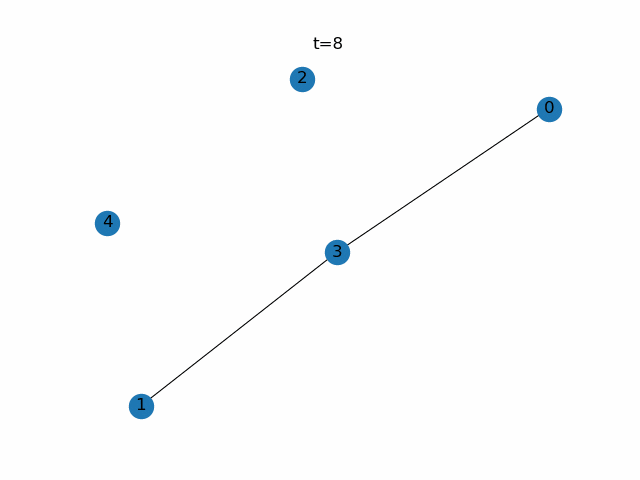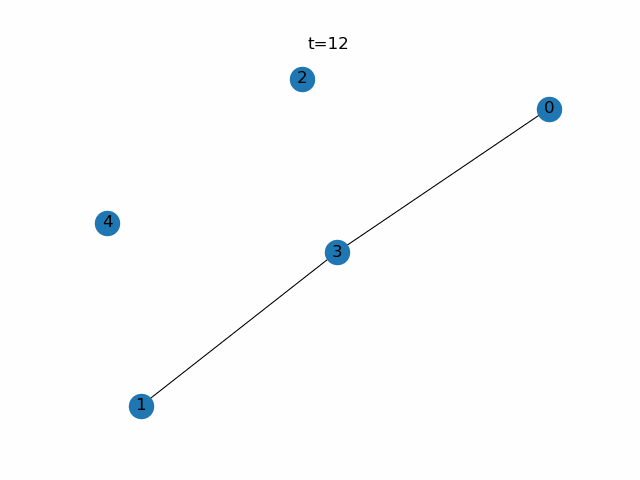
描画

%matplotlib nbagg
fig=plt.figure()

datatype=[('conductivity',float)]

def animate(i):
    A=np.matrix(conductivity[i],dtype=datatype)
    G=nx.from_numpy_matrix(A)
    weights=[G[u][v]['conductivity'] for u,v in G.edges()]
    
    plt.cla()
    nx.draw_networkx(G,pos,width=weights)
    plt.axis('off')
    plt.title('t=' + str(i))
    #plt.show()
    
anim = FuncAnimation(fig,animate,frames=nt,repeat=True)
#anim.save("nenkin01.gif", writer='pillow',fps=6)
plt.show()

もっと複雑なグラフで試す

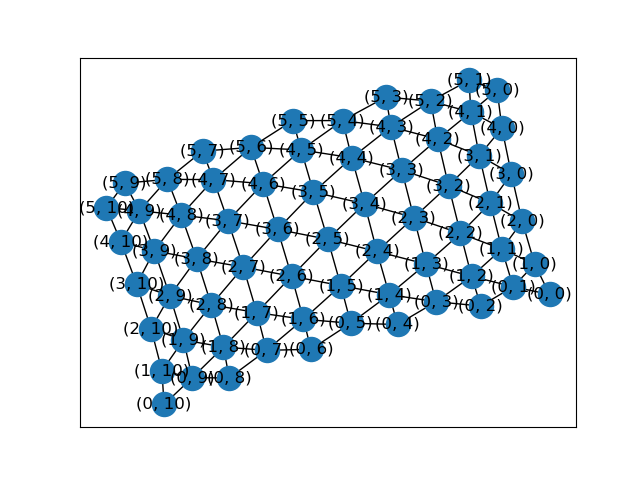
はじめに適当なグラフを作ります。

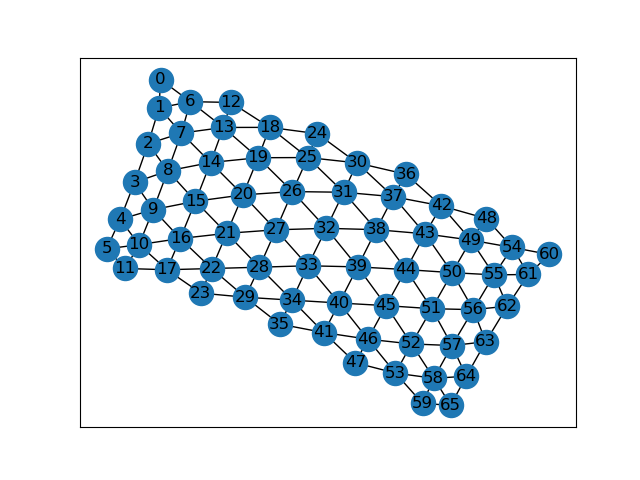
G0=nx.triangular_lattice_graph(10,10)
pos0=nx.spring_layout(G0)
nx.draw_networkx(G0,pos0)
plt.show()

生成したグラフは頂点のキー名が(0,0),(0,1),,,になっててこのままだと今回作ったプログラムでは使えないので、一度隣接行列に落とし、その隣接行列からグラフを再生成するというまわりくどいことをします。

nbr_mtx=nx.to_numpy_matrix(G0)
G=nx.from_numpy_matrix(nbr_mtx)
pos=nx.spring_layout(G,iterations=100)
nx.draw_networkx(G,pos)
plt.show()

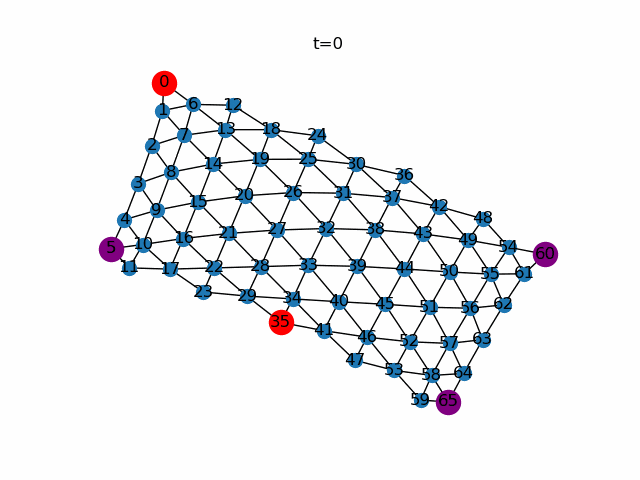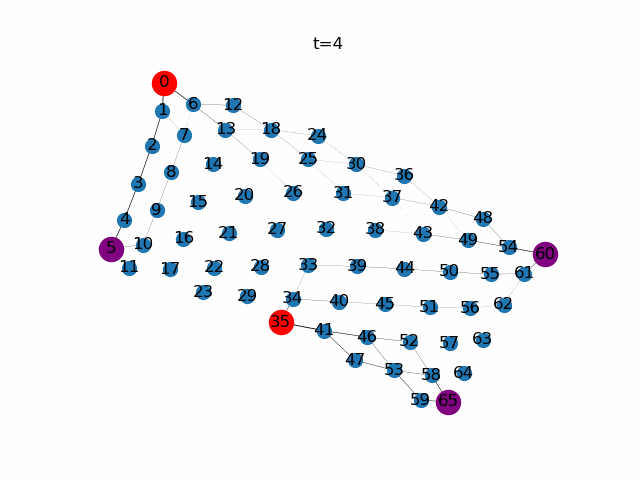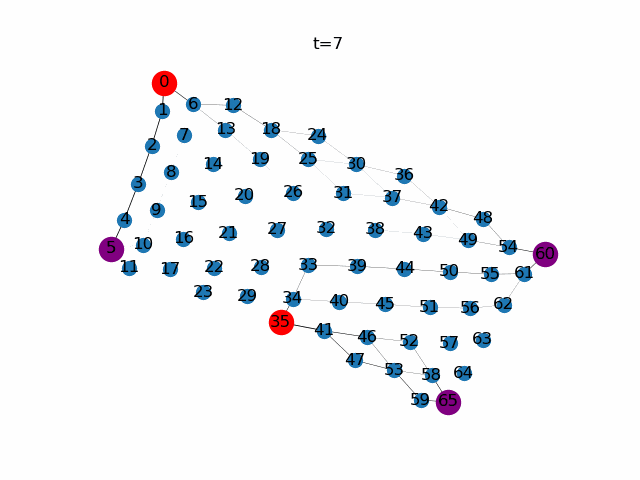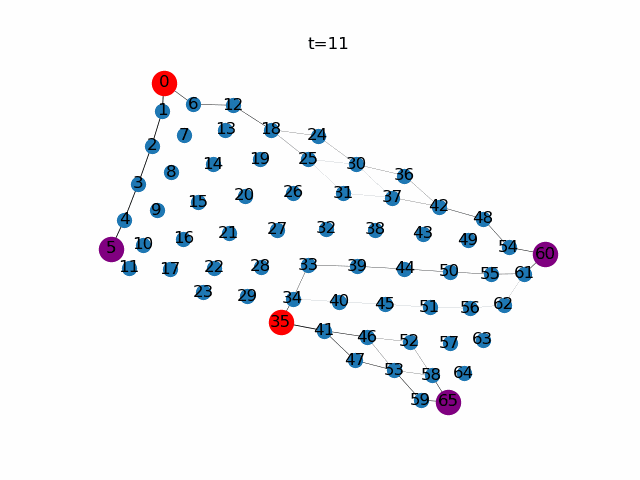
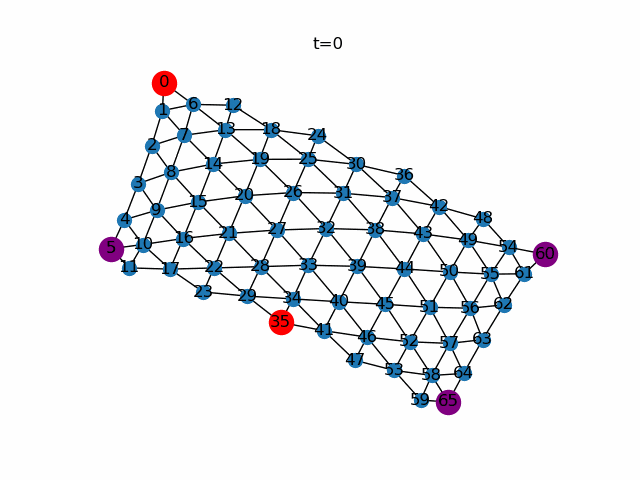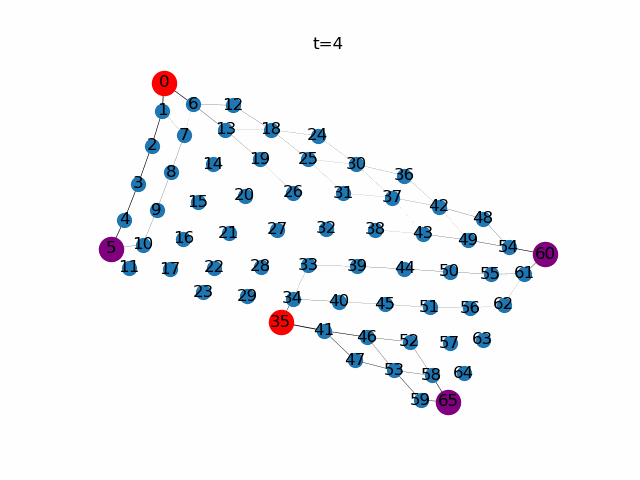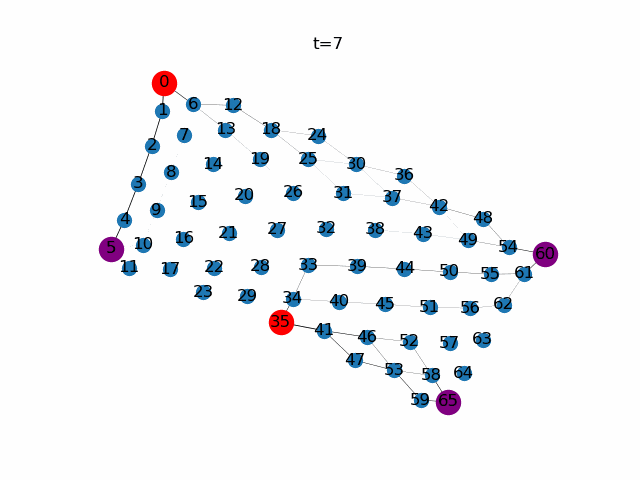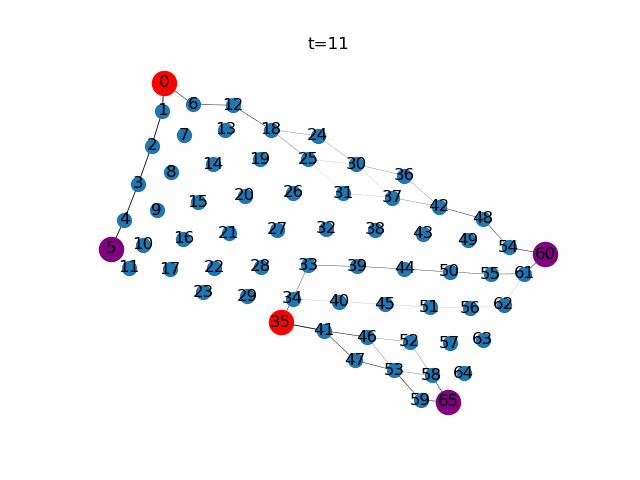
次に、餌ノードと任意に選択します。ここではノード0,35を餌ノード(Source),ノード5,60,65をもうひとつの餌ノード(Sink)としています。餌ノードが複数になっても粘菌ネットワーク全体で餌の量が保存されるように餌ノードの生産量を調整しています。

計算

import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import PillowWriter, FuncAnimation

#変数宣言
nt=12
#dt=1とする
nnodes=nx.number_of_nodes(G)
edge_list=list(G.edges)
nbr_mtx=nx.to_numpy_matrix(G)

conductivity=np.zeros((nt,nnodes,nnodes)) #D
length=np.zeros((nnodes,nnodes)) #L
pressure=np.zeros((nt,nnodes)) #p
flux=np.zeros(nnodes) #Q

#初期値と定数の設定
conductivity[0]=nbr_mtx #各エッジの流れやすさは最初1.0
length=nbr_mtx #今回は各エッジの長さは1.0とする
I0=2.0
source_list=[0,35]
sink_list=[5,60,65]
source_len=len(source_list)
sink_len=len(sink_list)

for i in source_list:
    flux[i]=I0

#餌ノードの量が全体で保存されるように調整する
for i in sink_list:
    flux[i]=-I0*(source_len/sink_len)

gamma=1.5

#ゼロ除算が発生しないように非ゼロ要素のみで割り算を行う
def divide_non_zero_element(D,L,num_nodes,list_edges):
    X=np.zeros((num_nodes,num_nodes))
    for i,j in list_edges:
        X[i,j]=D[i,j]/L[i,j]
        X[j,i]=D[j,i]/L[j,i]
    return X

#f(Q) for dD/dt 
def f(x):
    powered=x**gamma
    return powered/(powered+1)

#Dの時間変化量を求める
def dD(D,L,p,num_nodes,list_edges):
    X=divide_non_zero_element(D,L,num_nodes,list_edges)
    Q=np.multiply(X,np.expand_dims(p,axis=1)-p)
    ans=f(np.abs(Q))
    return ans

#一次連立方程式を解きpを求める
def deduce_p(D,L,B,num_nodes,list_edges):
    Y=divide_non_zero_element(D,L,num_nodes,list_edges)    
    A=np.diag(np.sum(Y,axis=1))-Y
    p=np.linalg.solve(A,B)
    return p

#pの初期値を求める
pressure[0]=deduce_p(conductivity[0],length,flux,nnodes,edge_list)

#繰り返し計算する
for t in range(0,nt-1):
    conductivity[t+1]=dD(conductivity[t],length,pressure[t],nnodes,edge_list)
    pressure[t+1]=deduce_p(conductivity[t+1],length,flux,nnodes,edge_list)

描画

%matplotlib nbagg
fig=plt.figure()

datatype=[('conductivity',float)]

def animate(i):
    A=np.matrix(conductivity[i],dtype=datatype)
    G=nx.from_numpy_matrix(A)
    weights=[G[u][v]['conductivity'] for u,v in G.edges()]
    
    plt.cla()
    nx.draw_networkx(G,pos,width=weights,node_size=100)
    nx.draw_networkx_nodes(G,pos,nodelist=source_list,node_color='red')
    nx.draw_networkx_nodes(G,pos,nodelist=sink_list,node_color='purple')
    plt.axis('off')
    plt.title('t=' + str(i))
    #plt.show()
    
anim = FuncAnimation(fig,animate,interval=500,frames=nt,repeat=True)
#anim.save("nenkin02.gif", writer='pillow',fps=2)
plt.show()

粘菌数理モデルによる経路探索。赤色の頂点は餌ノード(Source)、紫色の頂点はもう一つの餌ノード(Sink)、青色の頂点はそれ以外であることを示しています。$\gamma$の値が小さいと比較的輸送効率の悪い経路に対して寛容になります。

課題

計算回数を重ねるとLinAlgError: Singular matrixがでて止まります。おそらく経路にあまり関係のないエッジで成分がゼロに近づきすぎ、行列$\boldsymbol{A}$がランク落ちして逆行列を持たなくなってしまうことが原因と考えられます。もう使いそうにないエッジを切り捨てるとか改良が必要です。

計算量について

ボトルネックはstep.2の連立方程式を解くプロセスです。頂点が$n$個のとき、普通に連立方程式を解くと$O(n^3)$です。LU分解(scipy.linalg.lu_solve)を使って連立方程式を解くと$O(n^2)$です。

今後やりたいこと

標高差の因子をいれたモデルを考える（低い位置には流れやすく高い位置には流れにくい）。

gif動画がループしないことについて

出力されたgif動画を他のプログラムで再生するとループせず最後のフレームで止まるのではないでしょうか。それはあなたのせいではありません。matplotlibのpillowWriterのバグです。matplotlib v3.1では修正される予定です。
https://github.com/t-makaro/animatplot/issues/24
ループするgif動画を保存したい場合はimagemagickをインストールし`writer='imagemagick``を使用してください。

参考文献

• A. Tero, R. Kobayashi, and T. Nakagaki, "Physarum solver - a biologically inspired method of road-network navigation -", Physica A Statistical Mechanics and its Applications 363. 115(2006).

• A. Tero, S. Takagi, T. Saigusa, K. Ito, D. P. Bebber, M. D. Fricker, K. Yumiki, R. Kobayashi, and T. Nakagaki, "Rules for biologically inspired adaptive network design", Science 327, 439(2010).

• 加藤由人、大谷紀子、”粘菌ネットワークを用いた時間枠制約付き巡回セールスマン問題の解法”、情報処理学会第77回全国大会、4T-03(2015).

• [Python を使ってお手軽に数学 gif を作ってみよう]
  (https://qiita.com/wakabame/items/c3648501eb0f2b921ddf)