Go to Qiita Advent Calendar 2024 Top
LoginSignup
20
10

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@STInverSpinel

JuliaでKuramoto model

Last updated at Posted at 2018-12-30

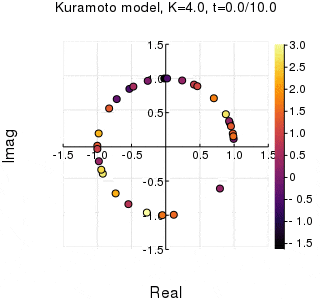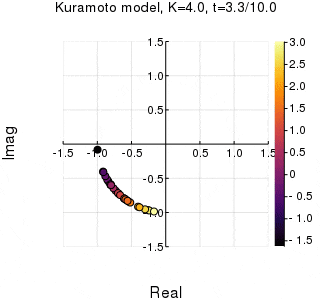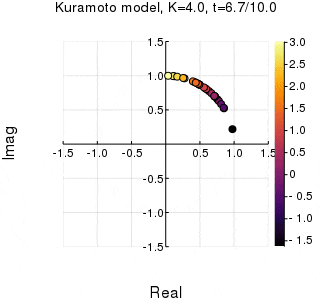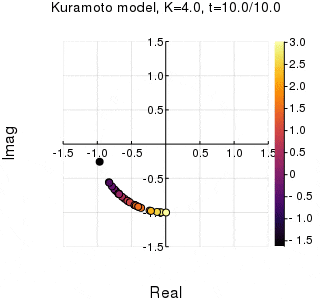
今回作るもの

Kuramoto_model2_K=4.gif

はじめに

世の中にはたくさんの同期(Synchronization)現象があります。例えば、大勢の人々が手拍子をうつとき、そのリズムは初めバラバラですが徐々にそろっていき、最後には一定のリズムになります。それは、拍手している人それぞれが周りの音を聞いて自分の拍子を調節しているからです。このような同期現象は、カエルの合唱、蛍の群れの発光、固定されていない板に乗せられたメトロノームの振り子などでも見られます。

この記事では、同期現象の代表的なモデルと知られている”蔵本モデル”について取り上げます。
具体的にやることというと、参考文献[1]をJuliaで実装することにチャレンジします。

蔵本モデル

蔵本モデルは京都大学の蔵本由紀教授により提案されました。このモデルは以下の微分方程式で表されます。

\frac{d \theta}{dt}=\omega_i+\frac{K}{N}\sum_{j=1}^{N}\sin(\theta_j-\theta_i)\\
(i=1,2,\cdots,N)

ここで、記号の意味を以下の表に表します。

記号 意味
$\theta$ 振動子の位相
$t$ 時間
$\omega_i$ $i$番目の振動子の自然振動数
$K$ 結合強度
$N$ 振動子の個数

$N$個の振動子があり、振動子はそれぞれがもつ自然振動数$\omega$にしたがって、位相$\theta$を単位時間ごとに変化させていきます。それだけではなく、自分以外の振動子$j$の位相と振動子自身$i$の位相との差$\theta_j-\theta_i$も位相の変化量に影響します。すなわち、$\theta_j$>$\theta_i$のとき、$\sin(\theta_j-\theta_i)$>$0$となり、$i$番目の位相変化量は増加します。反対に、$\theta_j$ < $\theta_i$のとき、$\sin(\theta_j-\theta_i)$<$0$となり、$i$番目の位相変化量は減少します。上記の微分方程式の右辺第2項は振動子どうしが群れをつくる（同期する）ようにはたらきます。その強度は$K$が大きいほど大きくなります。

計算

振動子の自然振動数$\omega$は正規分布（平均=1,分散=1）に応じてランダムに決定します。Juliaのrandn()は平均=0,分散=1の正規分布ですから1を足して平均をシフトさせておきます。位相$\theta$の初期値は0から2$\pi$の範囲で一様乱数から決定します。

計算はJupyter notebook上で行っています。はじめにモジュールと関数の定義を行います。

using LinearAlgebra
using Plots
gr(size=(320,300))

module KuramotoModel
struct Params
    N::Int64 #Size of Oscillator
    K::Float64 #binding strength
    dt::Float64 
    maxStep::Int64
    ω::Vector{Float64} #frequency
end

mutable struct Variables
    θ::Vector{Float64} #phase
end
end


function dθ(param,var)
    sum=zeros(param.N)
    for i in 1:param.N
        for j in 1:param.N
            sum[i]+=sin(var.θ[j]-var.θ[i])
        end
    end
    return (param.ω.+(param.K/param.N).*sum).*param.dt
end

function oneStep!(param,var)
    var.θ+=dθ(param,var)
    var.θ.%=2π
end

function draw(param,var,gen)
    t=round(gen*param.dt,digits=2)
    tmax=param.maxStep*param.dt
    K=param.K
    
    scatter(cos.(var.θ),sin.(var.θ),
        zcolor=param.ω,
        leg=false,
        cbar=true,
        xlabel="Real",
        xlims=(-1.5,1.5),
        ylabel="Imag",
        ylims=(-1.5,1.5),
        aspect_ratio=:equal,
        framestyle=:origin,
        title="KuramotoModel K=$K, t=$t/$tmax"
    )
end

別のセルで上記でつくったものを使い初期値を決めて計算します。

using Random
Random.seed!(2018)

using .KuramotoModel
function main(param,var)
    @time anim=@animate for m in 0:param.maxStep
        draw(param,var,m)
        oneStep!(param,var)
        end every 10
    
    @time gif(anim,"Kuramoto_model.gif",fps=10)
end

N=30
K=2.0
dt=0.01
maxStep=1000
ω=randn(N).+1.0 #mean=1,standard deviation=1
param1=KuramotoModel.Params(N,K,dt,maxStep,ω)

θ=rand(N).*2π
var1=KuramotoModel.Variables(θ)

main(param1,var1)

計算結果

maxStep=1000
4.200966 seconds (22.73 M allocations: 722.786 MiB, 3.64% gc time)
0.813532 seconds (488 allocations: 26.875 KiB)

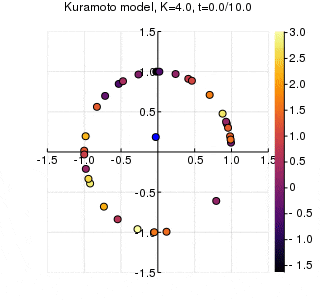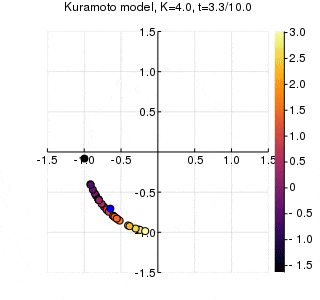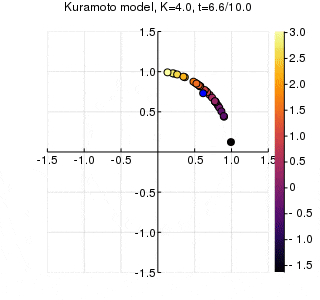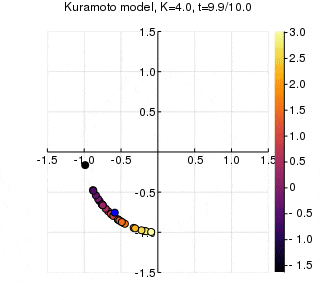
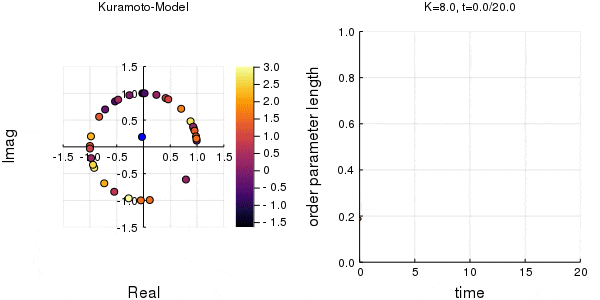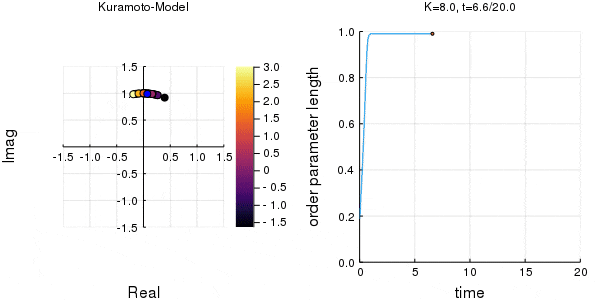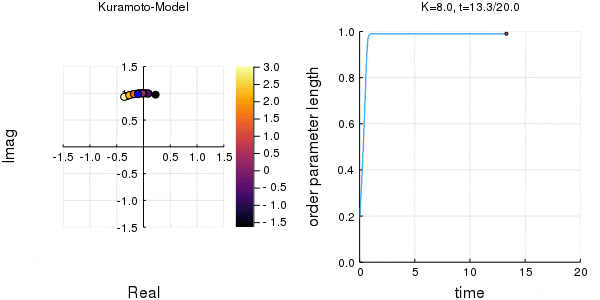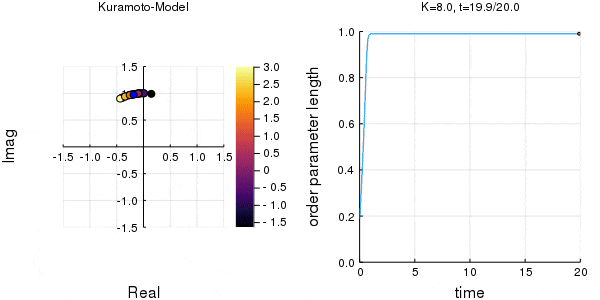
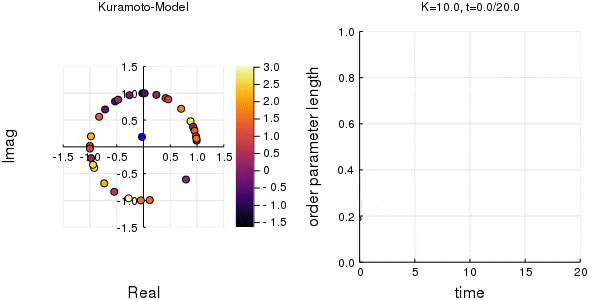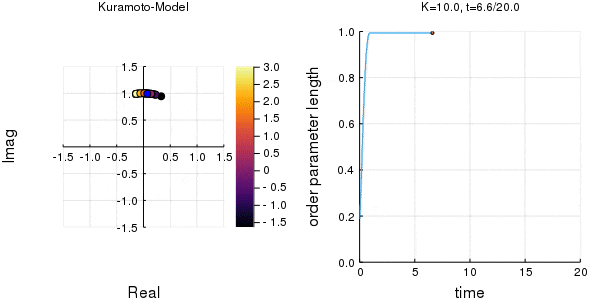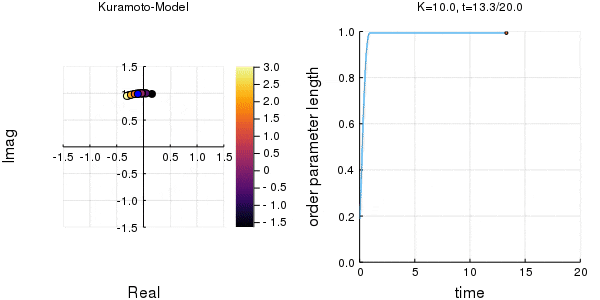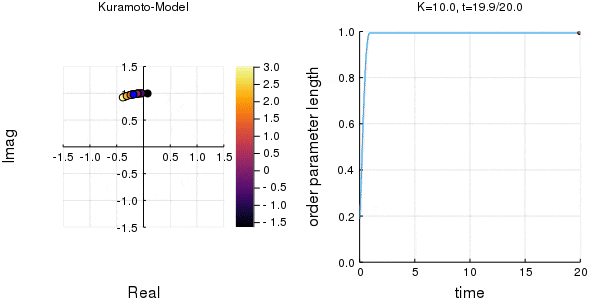
位相は単位円での位置、振動数はマーカーの色で表示しています。

Kuramoto_model1000_2.gif

秩序変数の導入

「どれくらい振動子が同期しているか」を定量的に議論するために秩序変数(order parameter)$\eta$を導入します。

\eta=\frac{\sum_{j=1}^{N}e^{i\theta_j}}{N}\\

これは複素数平面でいえば、振動子全ての重心です。秩序変数$\eta$の絶対値

r=|\eta|

の値を見れば振動子たちがどれくらい同期しているかが分かります。振動子が全然同期していなければ$r$は0に近く、同期しているほど$r$=1に近づきます。これを実装するためにコードに変更を加えます。

変更1. 変数に$\eta$, $r$, $t$を追加します。$\eta$の時間変化をグラフ化するため$\eta$, $t$は配列を使います。

mutable struct Variables
    θ::Vector{Float64} #phase
    η::Complex{Float64} #weight center
    r::Vector{Float64} #absolute value of η
    t::Vector{Float64} #time
end

変更2. 重心$\eta$を計算する関数をつくります。

function calcCenter(param,var)
    sum=0.0+0.0im
    for j in 1:param.N
        sum+=exp(1.0im*var.θ[j])
    end
    var.η=sum./param.N
end

変更3. 重心を青いマーカーでプロットします。

 plot!((real(var.η),imag(var.η)),
        seriestype=:scatter,
        mcolor=:blue)

変更4. 横軸に時間、縦軸に$r$をとった折れ線グラフをつくります。最新の値をマーカーでプロットします。

    q=plot(var.t,var.r,
        xlabel="time",
        xlims=(0.0,tmax),
        ylabel="order parameter",
        ylims=(0.0,1.0),
        title="K=$K, t=$t/$tmax"
    )
    
    scatter!((var.t[end],var.r[end]),
        ms=2,
        leg=false)

変更5. 計算した$\eta$の絶対値をrにpush!します。そのときの時刻もtに入れておきます。

@time anim=@animate for m in 0:param.maxStep-1
        calcCenter(param,var)
        push!(var.r,abs(var.η))
        push!(var.t,m*param.dt)
        draw(param,var,m)
        oneStep!(param,var)
        end every 10

最終的なコードを以下に示します。

モジュール作成セル
using LinearAlgebra
using Plots
gr(size=(600,300))

module KuramotoModel
struct Params
    N::Int64
    K::Float64
    dt::Float64
    maxStep::Int64
    ω::Vector{Float64}
end

mutable struct Variables
    θ::Vector{Float64}
    η::Complex{Float64}
    r::Vector{Float64}
    t::Vector{Float64}
end

end


function dθ(param,var)
    sum=zeros(param.N)
    for i in 1:param.N
        for j in 1:param.N
            sum[i]+=sin(var.θ[j]-var.θ[i])
        end
    end
    return (param.ω.+(param.K/param.N).*sum).*param.dt
end

function calcCenter(param,var)
    sum=0.0+0.0im
    for j in 1:param.N
        sum+=exp(1.0im*var.θ[j])
    end
    var.η=sum./param.N
end

function oneStep!(param,var)
    var.θ+=dθ(param,var)
    var.θ.%=2π
end

function draw(param,var,gen)
    t=round(gen*param.dt,digits=2)
    tmax=param.maxStep*param.dt
    K=param.K
    
    p=scatter(cos.(var.θ),sin.(var.θ),
        zcolor=param.ω,
        leg=false,
        cbar=true,
        xlabel="Real",
        xlims=(-1.5,1.5),
        ylabel="Imag",
        ylims=(-1.5,1.5),
        aspect_ratio=:equal,
        framestyle=:origin,
        title="Kuramoto-Model"
    )
    plot!((real(var.η),imag(var.η)),
        seriestype=:scatter,
        mcolor=:blue)
    
    q=plot(var.t,var.r,
        xlabel="time",
        xlims=(0.0,tmax),
        ylabel="order parameter length",
        ylims=(0.0,1.0),
        title="K=$K, t=$t/$tmax"
        #aspect_ratio=:equal
    )
    scatter!((var.t[end],var.r[end]),
        ms=2,
        leg=false)
    
    plot(p,q)
end
実行セル
using Random
Random.seed!(2018)

using .KuramotoModel
function main(param,var)
    @time anim=@animate for m in 0:param.maxStep-1
        calcCenter(param,var)
        push!(var.r,abs(var.η))
        push!(var.t,m*param.dt)
        draw(param,var,m)
        oneStep!(param,var)
        end every 10
    
    @time gif(anim,"Kuramoto_model.gif",fps=10)
end

N=30
K=4.00
dt=0.01
maxStep=2000
ω=randn(N).+1.0 #mean=1,standard deviation=1
param1=KuramotoModel.Params(N,K,dt,maxStep,ω)

θ=rand(N).*2π
cent=0.0+0.0im
r=[]
t=[]
var1=KuramotoModel.Variables(θ,cent,r,t)

main(param1,var1)

計算結果

実行時間（例）maxStep=2000
19.701497 seconds (110.43 M allocations: 3.607 GiB, 4.24% gc time)
1.123443 seconds (486 allocations: 26.875 KiB)

$K$を1.0, 2.0, 2.63, 4.0, 8.0, 10.0と変えて計算しました。Kが大きくなるほど同期に至るのが早くなり同期具合も強いことが分かります。
左のグラフの、真ん中でうろうろしている青い点が$\eta$です。
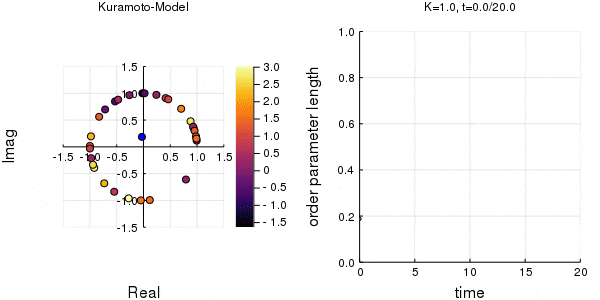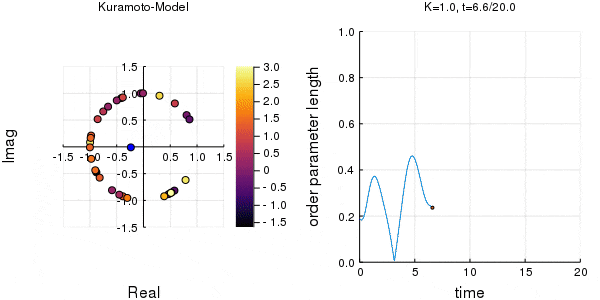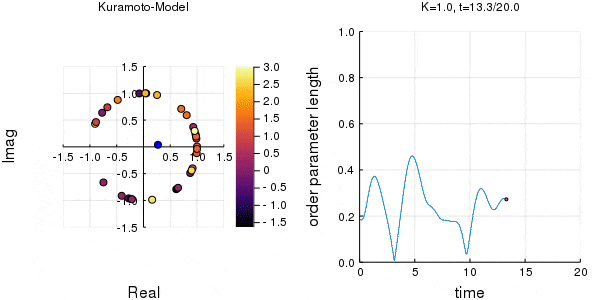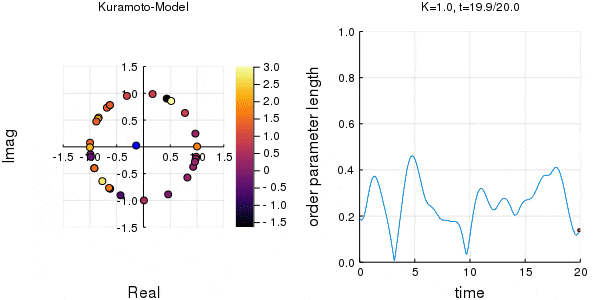
Kuramoto_model1_K=1.gif
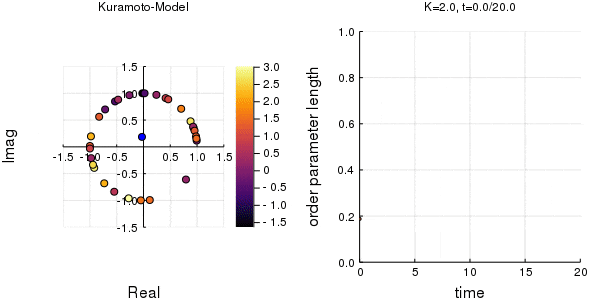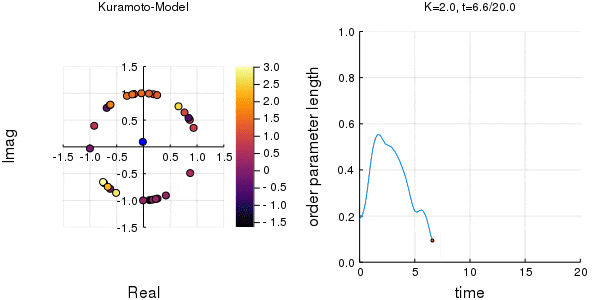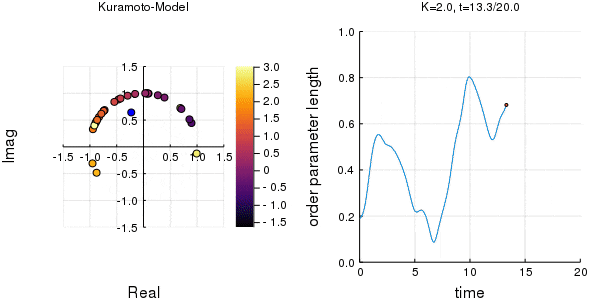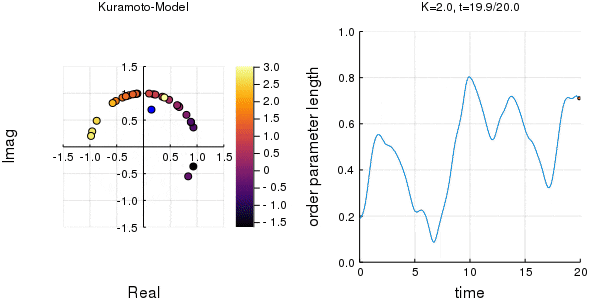
Kuramoto_model1_K=2.gif
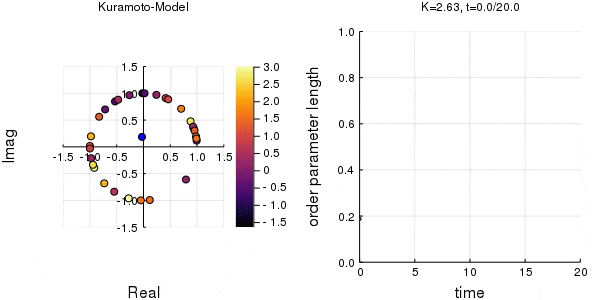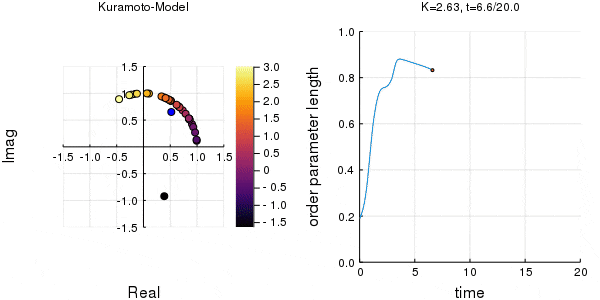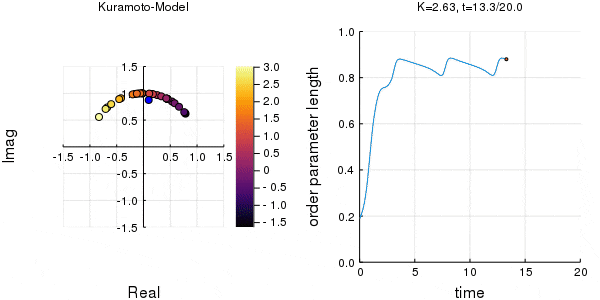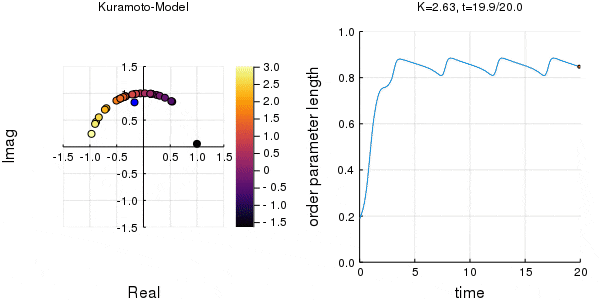
Kuramoto_model1_K=Kc.gif
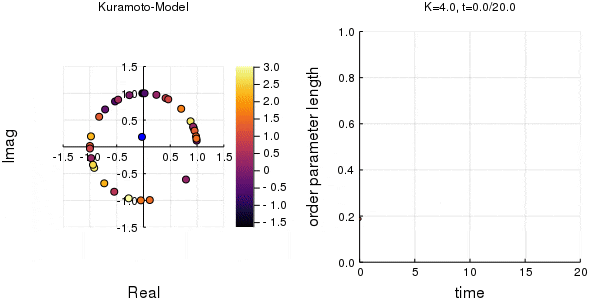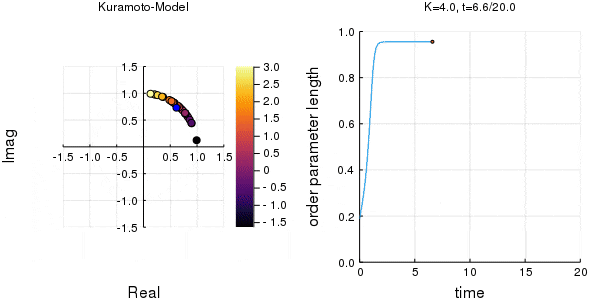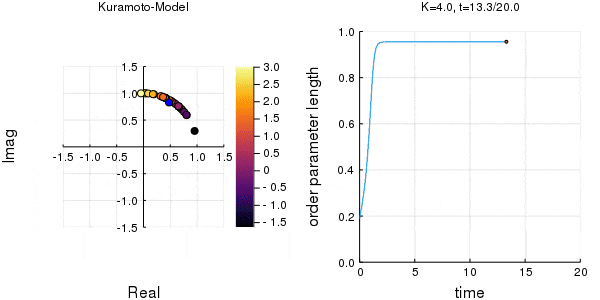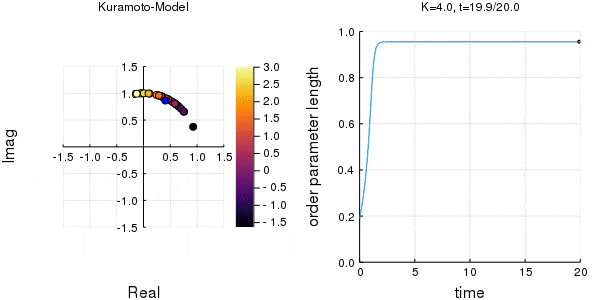
Kuramoto_model1_K=4.gif
Kuramoto_model1_K=8.gif
Kuramoto_model1_K=10.gif

蔵本転移点

秩序変数$r$は結合強度$K$の増加に従って単調増加するのではなく、ある閾値をもちます。その閾値を蔵本転移点と呼び、$K_c$で表します。
今回の系では、振動数分布は正規分布に従って分布しているため、$N\rightarrow \infty$とみなすと、閾値は

K_c=\frac{2}{\pi g(0)}

に近い値になると思われます。ここで$g(\omega)$は確率密度関数です。
今回は正規分布を使用しましたから、$g$に正規分布を代入してみましょう。

g(\omega)=\frac{1}{\sqrt{2\pi \sigma^2}} \exp(-\frac{(\omega-\mu)^2}{2})

であり、平均$\mu$=1, 分散$\sigma$=1, $\omega$=0のとき

\displaylines{
g(0)=\frac{1}{\sqrt{2\pi}} \exp(-\frac{1}{2}) \\
K_c=\frac{2}{\pi g(0)}\approx2.63
}

です。上の節でK=2.63のときの計算を行ったのはこのような背景があるためです。

参考文献

20
10
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
20
10

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?