シミュレーションにおける微分方程式の計算方法
本記事では、差分空間で作成されるシミュレーション(有限差分法)において微分方程式を算出するための知識やプログラムの書き方を紹介します。実際自分自身がシミュレーションを構築する際に気になった点や注意する点を備忘録的にまとめたので参考にしてみてください。また本記事では微分方程式の数学的な知識については省略してる部分も多いので注意してください。
※本記事ではpythonをベースにプログラムを記述します。
目次
有限差分法における関数表現
有限差分法とは簡単に言えば写真のようなものです。古い写真を拡大すると画像が荒いと感じることも多いのではないでしょうか。これは、写真は現実に見える情報を連続的に表現しているのではなく、画素という小さな情報の集合体でるからです。これを言い換えれば、写真は現実の連続的情報を離散的に近似したものだと考えることもできます。この離散化する(情報を連続的では無く飛び飛びで表す)といものを関数においてもあてはめると有限差分法を理解しやすいのではないでしょうか。そこで、実際の関数と離散化された差分表現による関数の図を示します。
実際の関数(連続関数)と差分関数の関係
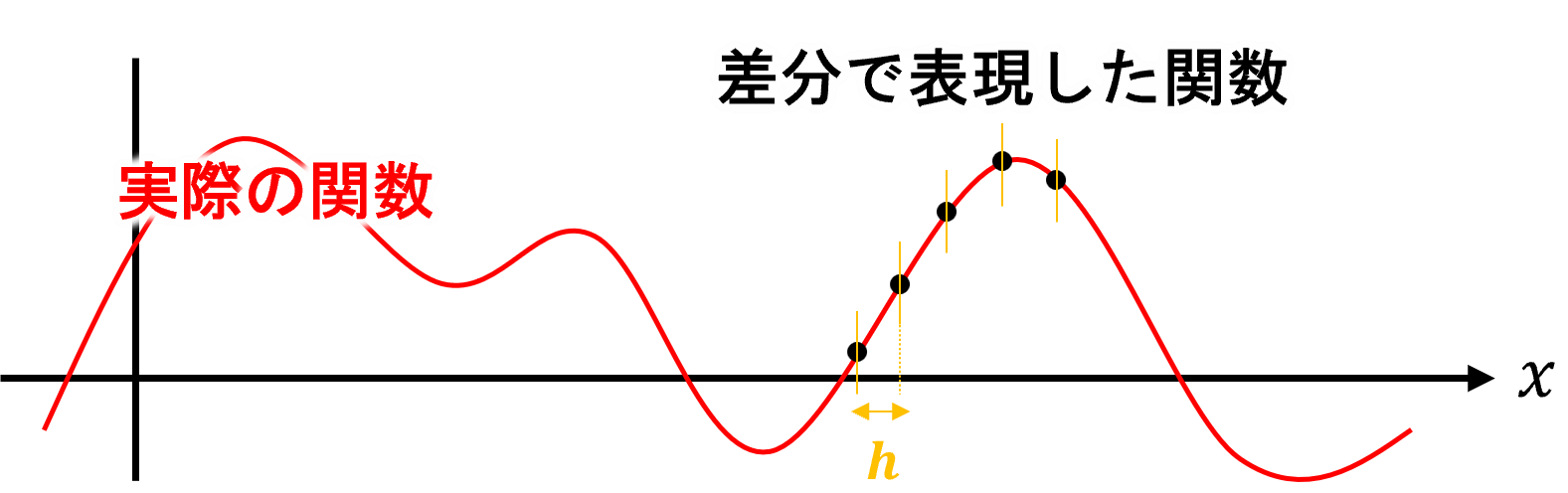
図からも分かるように、実際の関数は赤色で示されるような連続的な関数であるのに対して、差分表現では黒い点のように部分的な情報のみを保持しています。この差分間隔hを小さくしていくことで現実の状態を再現しようと試みることが基本的な有限差分法の考え方になります。このように、有限差分法における関数は現実の連続関数を一定の間隔(一定でない場合もあり)でプロットしたように表現されます。実際のシミュレーションではこのような不連続な関数を用いて微分方程式の解を算出する場面が多々あります。
差分空間における微分方程式
ここまでの通り、差分空間では不連続な関数が取得できますが、この不連続な関数を用いてどのように微分方程式を定義することが正しいのでしょうか。まずここで、一般的に用いられる1次・2次の微分方程式を次に示します。
1次の前進差分
f^{(1)}(x)=\frac{f(x+h)-f(x)}{h}
1次の後進差分
f^{(1)}(x)=\frac{f(x)-f(x-h)}{h}
1次の中心差分
f^{(1)}(x)=\frac{f(x+h)-f(x-h)}{2h}
2次の前進差分
f^{(2)}(x)=\frac{f(x+2h)-2f(x+h)+f(x)}{h^{2}}
2次の中心差分
f^{(2)}(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^{2}}
通常のシミュレーションでは上記の微分方程式が良く用いられています。ここで疑問に思うのが、この微分方程式はどのように求めることができるのかという点です。実際、シミュレーションによってはより精度の高い近似解を算出する為に採用する微分方程式をより複雑なものとする場合もあります。
One-side difference in 2nd difference
f^{(2)}(x)=\frac{2f(x)-5f(x+h)+4f(x+2h)-f(x+3h)}{h^{2}}
Slanted difference in 2nd difference
f^{(2)}(x)=\frac{11f(x-h)-20f(x)+6f(x+h)+4f(x+2h)-f(x+3h)}{12h^{2}}
場合によってはこのような複雑な微分方程式を用いることも、算出法を知っていれば全く難しいものではありません。そこでこのような微分方程式を算出する方法を、One-side difference in 2nd differenceを例にとって説明していきたいと思います。この算出法では、何次の微分方程式を求めたいのか、自分自身(x)に対してどの項((x+h), (x-h), ...)を使って微分方程式を算出したいのかの2つを決めるだけでどんな微分方程式も算出することが出来るようになります。
1. 自身を除いた必要な項数分のテイラー展開を行う
One-side difference in 2nd differenceの場合は x+h, x+2h, x+3h が必要になります。この際、テイラー展開は最低でもn次以上行ってください。
f(x+h)=f(x)+hf^{(1)}(x)+\frac{h^{2}}{2}f^{(2)}(x)+\frac{h^{3}}{6}f^{(3)}(x)+\frac{h^{4}}{24}f^{(4)}(x)+...
f(x+2h)=f(x)+2hf^{(1)}(x)+\frac{4h^{2}}{2}f^{(2)}(x)+\frac{8h^{3}}{6}f^{(3)}(x)+\frac{16h^{4}}{24}f^{(4)}(x)+...
f(x+3h)=f(x)+3hf^{(1)}(x)+\frac{9h^{2}}{2}f^{(2)}(x)+\frac{27h^{3}}{6}f^{(3)}(x)+\frac{81h^{4}}{24}f^{(4)}(x)+...
テイラー展開
f(x+h)=f(x)+hf^{(1)}(x)+\frac{h^{2}}{2!}f^{(2)}(x)+...+\frac{h^{n}}{n!}f^{(n)}(x)+...
2. n次の項に関して解く
今回は2次について解いてみる。
f^{(2)}(x)=\frac{2f(x)-5f(x+h)+4f(x+2h)-f(x+3h)}{h^{2}}+h^{3}\left\{\frac{1}{6}\cdot 0+\frac{h}{24}\cdot (-22)+...\right\}
3. 微小項(h→0)を無視することで答えを得ることが出来る
f^{(2)}(x)=\frac{2f(x)-5f(x+h)+4f(x+2h)-f(x+3h)}{h^{2}}
微分方程式を算出するアルゴリズム
有限差分法における微分方程式を算出する際に注意すべきは境界問題である。最初に説明したように有限の差分空間は画像のように端が存在する。この端では自分自身に対して端側に位置する部分をどのように定義するかを考える必要がある。つまり、端におけるx+hを定義する必要がある。基本的には定義の仕方は大きく二つあり、開境界と周期境界である。開境界では、端における隣を自分自身もしくは存在しないものとして取り扱う必要がある。この部分では微分方程式の定義を変更する必要があるのが開境界である。一方、周期境界では左端と右端が連続しているように周期的な空間を定義することができる。この空間では、空間内の現象が周期的に連続するという仮定が必要があるのが注意すべき点である。ここでは、開境界においては隣を自分自身と置き換える場合のアルゴリズムを周期境界におけるアルゴリズムと合わせて紹介する。
例えば下記のような1次の微分方程式を考える。
# xcell, ycellはそれぞれセル数を表す
# xsize, ysizeはそれぞれセルの長さを表す
for x in range(xcell):
for y in range(ycell):
xp, xm, yp, ym = next_xy(x,y,xcell, ycell)
fx = (f[xp,y]-f[xm,y])/(2.0*xsize)
fy = (f[x,yp]-f[x,ym])/(2.0*ysize)
ここでは、x,yに対する隣接セルをnext_xy()によって取得している。このとき、next_xy()は次のように定義することが出来る。
開境界
def next_xy(x: int,y: int,xcell: int, ycell: int):
if x == 0:
xp = x+1; xm = x
elif x == xcell-1:
xp = x; xm = x-1
else:
xp = x+1; xm = x-1
if y == 0:
yp = y+1; ym = ycell-1
elif x == ycell-1:
yp = y; ym = y-1
else:
yp = y+1; ym = y-1
return xp, xm, yp, ym
周期境界
def next_xy(x: int,y: int,xcell: int, ycell: int):
if x == 0:
xp = x+1; xm = xcell-1
elif x == xcell-1:
xp = 0; xm = x-1
else:
xp = x+1; xm = x-1
if y == 0:
yp = y+1; ym = ycell-1
elif x == ycell-1:
yp = 0; ym = y-1
else:
yp = y+1; ym = y-1
return xp, xm, yp, ym
また、実際にシミュレーションを利用する際には微分方程式は何度も呼び出されることも多いので、次のようにあらかじめ xp, xm, yp, ym の解を算出ることで速度を向上させることも可能です。
import numpy as np
xp = np.zeros((xcell, y_cell), dtype="int32")
xm = np.zeros((xcell, y_cell), dtype="int32")
yp = np.zeros((xcell, y_cell), dtype="int32")
ym = np.zeros((xcell, y_cell), dtype="int32")
for x in range(xcell):
for y in range(ycell):
xp[x,y], xm[x,y], yp[x,y], ym[x,y] = next_xy(x,y,xcell, ycell)
このようにして定義した隣接セルを用いて2次の微分方程式を表現すると次のようになります。
# xcell, ycellはそれぞれセル数を表す
# xsize, ysizeはそれぞれセルの長さを表す
for x in range(xcell):
for y in range(ycell):
fxx = (f[xp[x,y],y] + f[xm[x,y],y] - 2.0*f[x,y])/(xsize*xsize)
fyy = (f[x,yp[x,y]] + f[x,ym[x,y]] - 2.0*f[x,y])/(ysize*ysize)
fxy = (f[xp[x,y],yp[x,y]] + f[xm[x,y],ym[x,y]] - f[xp[x,y],ym[x,y]] - f[xm[x,y],yp[x,y]] )/(4.0*xsize*ysize)
このようにアルゴリズムを書くことでさまざまなシミュレーションで微分方程式を定義することが可能となります。上記の例では隣接セルのみ取り扱いましたが、必要に応じて+2, +3といった遠いセルを用いて微分方程式を求めることでより精度の高い結果を得ることが可能な場合もあるので参考にしてみてください。
おわりに
この記事で取り扱った知識は実際にシミュレーションを作成する、もしくは既存のシミュレーションを使うときに分かっているようでわかっていない場合もあるかと思います。この記事がそういった方の少しでも役に立つことがあればうれしく思います。
最後までご覧いただきありがとうございます。