Homcloudを利用した画像解析の注意点
本記事では Persistent Homology(PH) に基づく解析ソフト HomCloud を画像解析に利用する際の注意点を解説しています。画像解析に本ソフトを利用する際には通常の点群で取り扱うPH解析と比較して制約条件が発生してしまうので、以下の記事を参考にしながら利用してみてください。
また本記事では2値化画像(白黒)かつ0次元のPHを用いた解析を前提として説明しているので注意してください。
※Persistent Homologyに関する説明はここでは省略するので、興味がある方は以下のサイトを参照してみてください。
※随時更新しています。(最新:2022/12/14)
目次
画像とPDの対応関係
Persistent Diagram(PD)は画像内のトポロジー情報をbirth-deathペアとして記録するモノですが、画像で扱う際にはどのような画像的特徴が保存されるのかを理解することが必要です。以下の画像はHomcloudを画像解析として用いた際の形状情報とPDとの対応関係を示したものです。
画像とPDの対応関係[1]
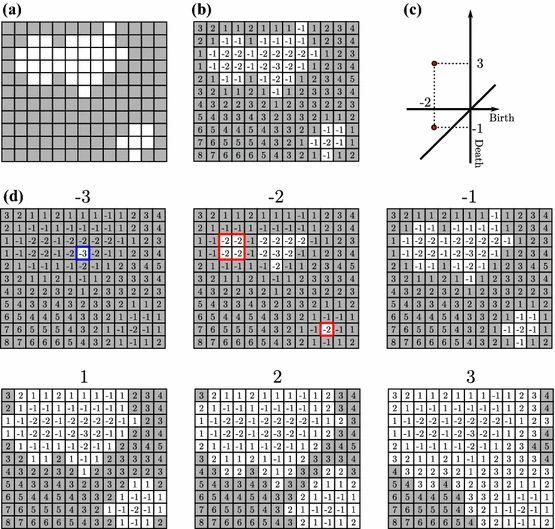
上記の図から白い構造の連結性がPD上の左下の領域に、構造間の位相関係がPD上の左上の領域にプロットされていることが分かります。つまり、連結した構造は構造を縮小する(deathが負)ことで、離れた構造は構造を拡大する(deathが正)ことで表現しています。(白黒境界を基準としたフィルトレーションを縮小に対して負、拡大に対して正として考えると理解しやすいです。)これらPDと画像の関係性を表現すると次のようになります。deathが正の領域では離れた構造が、deathが負の領域では連結した構造が保存されていることがよくわかります。また、birthの大きさは構造の大きさを示しており、これらを組み合わせた情報から構造の定量的特徴を取得することが出来ます。
構造的特徴とPDの対応関係[1]
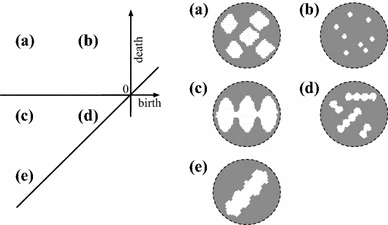
しかし、これらの模式的な関係性のみでは実際の構造的特徴とPDの対応関係を詳細に理解することは難しいです。そこで、様々な構造を画像として構築し、実際にHomCloudを用いて算出されたPDとの対応関係を見ていきたいと思います。
画像内に1つの構造情報のみを含む場合
HomCloudの利用時に注意する必要があるのは、『reduced persistence diagram』というものです。[1] の論文に"Note that the first connected component born at −3 is removed in the reduced persistence diagram." のような記載がありますが、これは構造の中で基準となる最も大きな構造はPD図から除かれるというものです。つまり、2値化画像解析においては、実際に算出されるPD上に含まれる情報は実際の"構造数-1"であるということです。
では、実際に大きな構造を一つのみを持つ画像を生成して試してみたいと思います。一つの構造と認識されるための最も簡単な考え方は境界から等距離の位置に中心が存在する構造です。そこで、半径の異なる円を用意し、実際のPDとの対応関係を以下に示します。
1つの構造情報(円)のみを持つ画像とPDとの対応関係(aは画像をbは画像に対応したPDをそれぞれ示している)
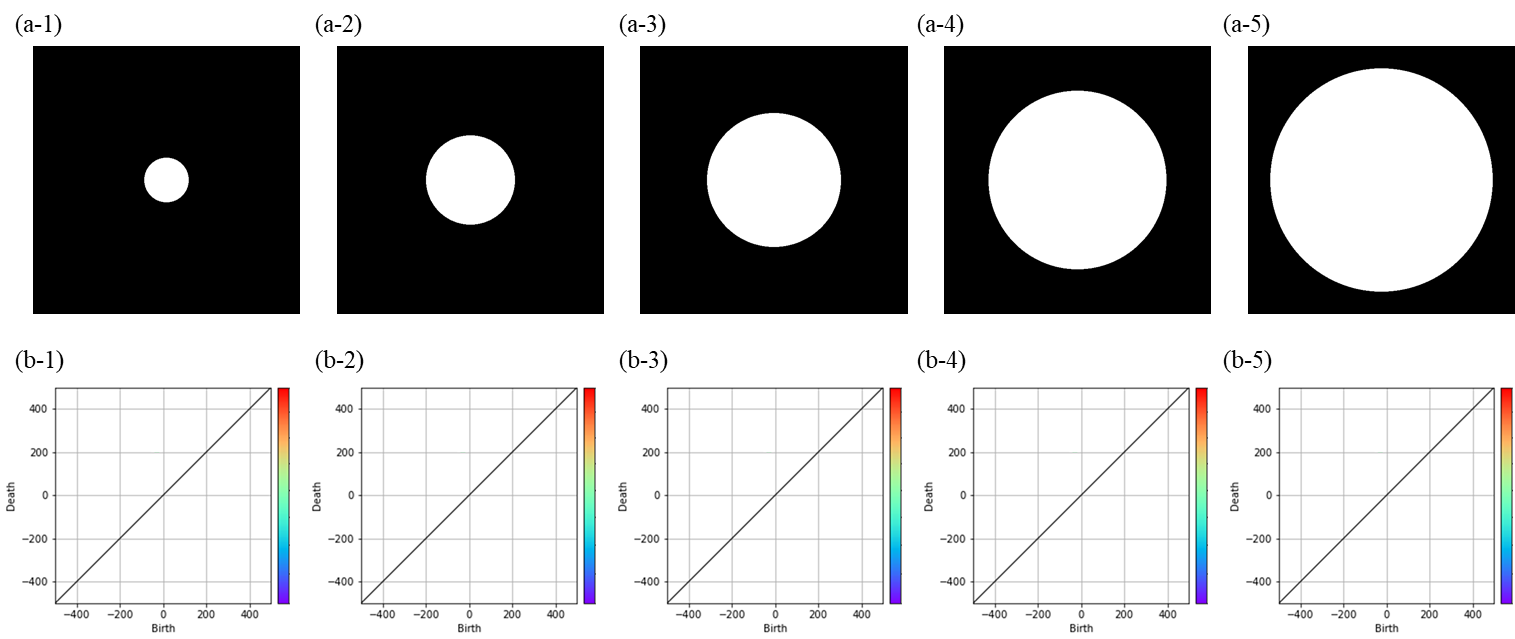
画像からも分かるように、全ての画像に対してPD上にプロットが表示されていないことが分かります。実際には、PD上にプロットが存在しない場合はエラーとなることもあるので、その場合は適切な例外処理などが必要となります。
また、上記のような構造の他にも、次のような構造も一つの構造情報として認識されるため注意が必要です。
1つの構造情報のみを持つ画像とPDとの対応関係2(aは画像をbは画像に対応したPDをそれぞれ示している)
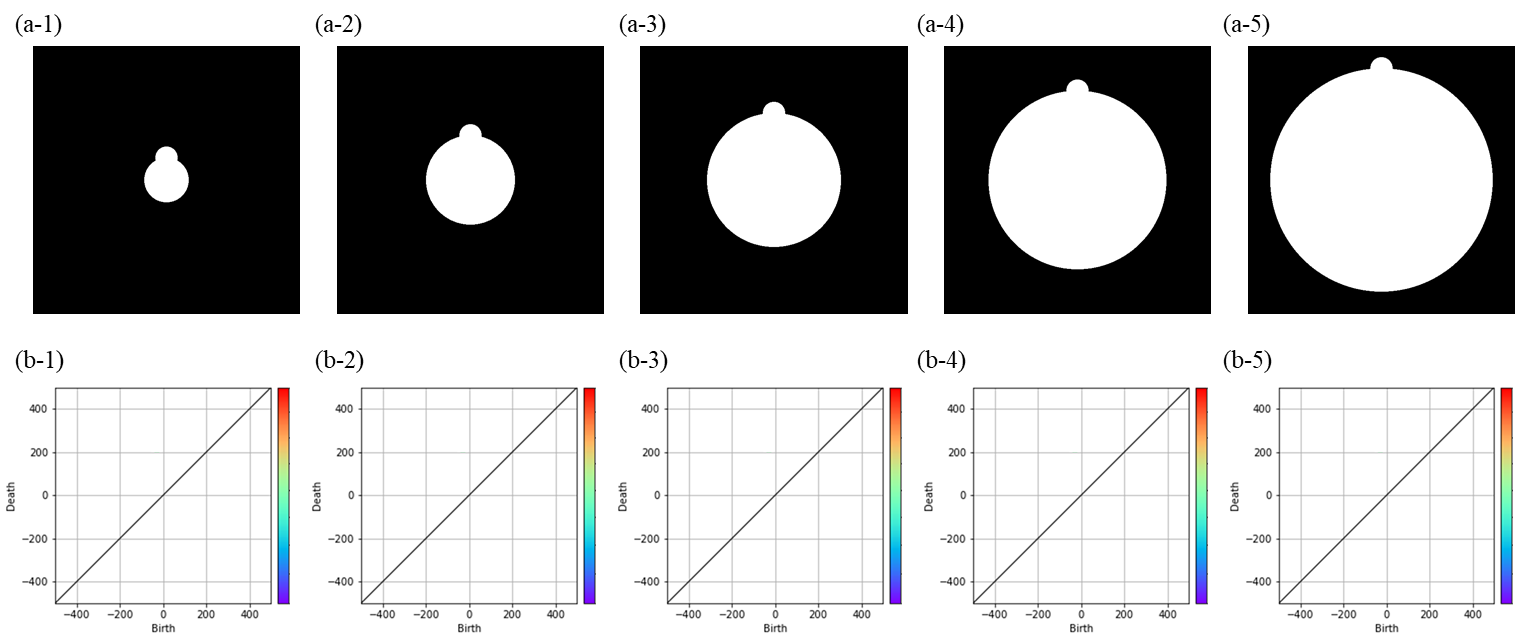
この構造では、一見円構造に対して突起が連結しているように思いますが、境界からフィルトレーションを考えると、小さな突起は連結した成分ではなく大きな円の一部として認識されてしまうためPD上にプロットが存在しないこととなります。このように、『reduced persistence diagram』が導入されていることで、基準となる構造の情報が取得できていないこと、また基準となる構造には一見連結したように見える構造が含まれる場合もあることに注意してください。(実際には上記のような構造は形成されにくいと思いますが、常に構造との対応関係を意識して解析することが重要です。)
画像内に2つの構造情報を含む場合
次に、2つの構造を持つ場合について考えていきたいと思います。2つの構造を持つ場合では、『reduced persistence diagram』の考え方に従い、1つの構造情報のみを取得することが出来ます。この構造情報は連結している場合にはdeathが負のデータとして、離れた構造の場合にはdeathが正の情報として記録されます。ここでは離れた構造の例を用いて解説したいと思います。ここでは説明のために以下の2つの構造パターンを用います。
2つの構造情報を持つ画像とPDとの対応関係(aは画像をbは画像に対応したPDをそれぞれ示している)
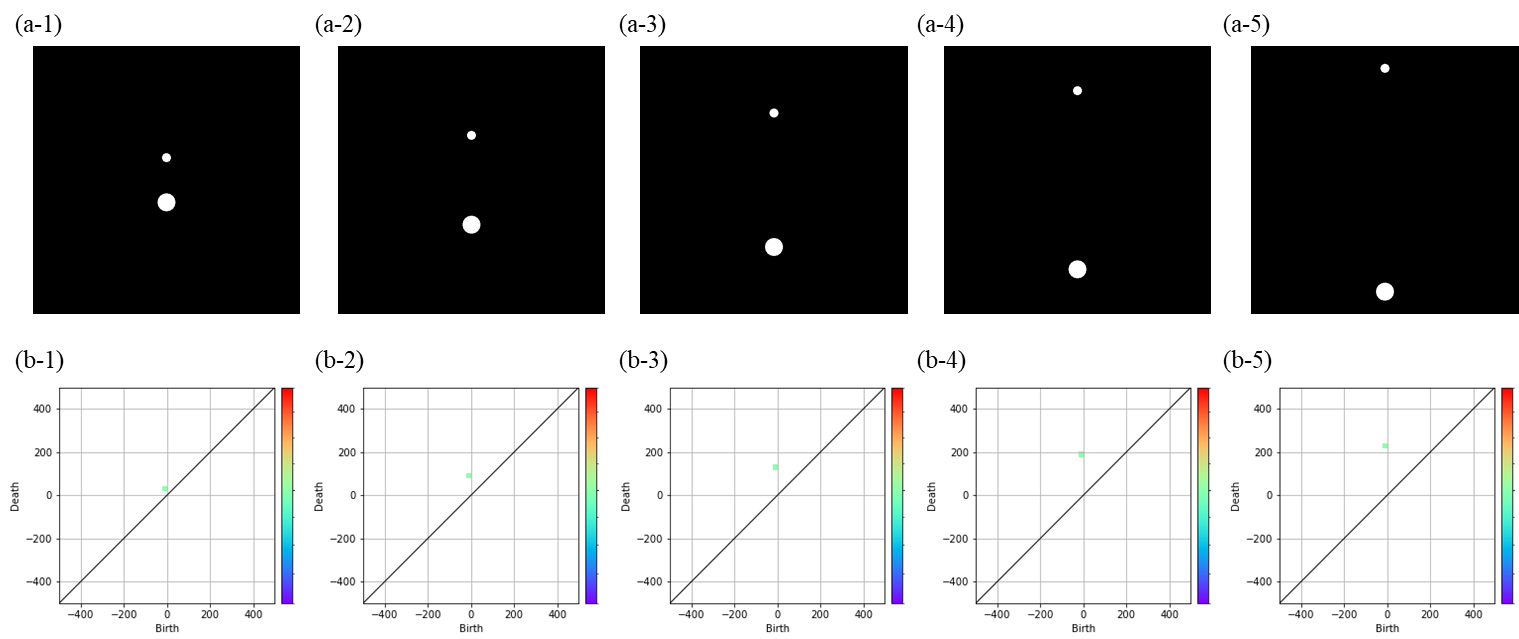
2つの構造情報を持つ画像とPDとの対応関係2(aは画像をbは画像に対応したPDをそれぞれ示している)
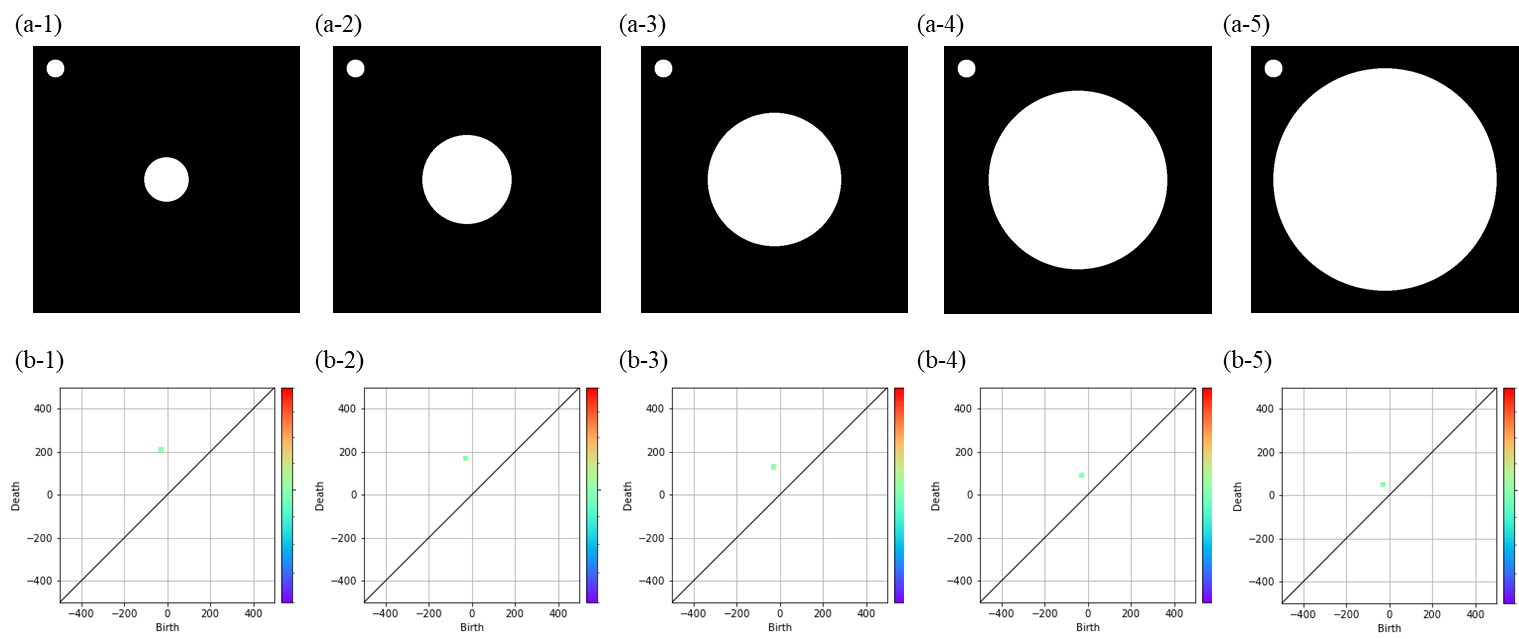
まず1つ目の対応関係では、2つの構造の大きさは変化させずに構造間の距離を変化させています。まず『reduced persistence diagram』によって下側の大きい構造情報は捨てられ、上側の構造のみがプロットされるためPD上には1点のみ存在していることが分かります。構造間の距離が離れることでPD上の点はbirthが一定、deathが大きくなる様子が観察できます。これはbirthは構造の大きさを示しており、deathは構造間の位相関係を示すことからこのような結果となると言えます。deathが示す位相関係は境界間の距離という認識が一番近く、中心距離を示していないことには注意が必要です。
2つ目の対応関係では、2つの構造間の中心距離は一定に、基準となる構造の大きさを変化させています。PDを見ると、基準構造が大きくなることでdeathの値が小さくなっていることが分かります。これは、構造の拡大に伴って2つの構造間の境界距離が短くなっている様子を示しており、このことからも、deathが示す位相関係は境界間の距離という認識が一番近く、中心距離を示していないことが分かると思います。
このように離れた構造間では構造の大きさと位相関係を主に抽出していることが分かります。ここでは連結成分を持たない構造(円)のみを用いて議論を行っていますが、実際の構造の多くは連結成分を同時に含むため、位相関係と連結成分の2つを総合的に考慮することが求められます。
画像内に多数の構造情報を含む場合-連結成分なし-
次に、連結成分を持たない多数の構造(円)を含む場合について考えます。これは相互作用によって分散した粒子のようなものを考えるとわかりやすいかもしれません。ここでは条件として各構造の大きさは一定の大きさの範囲でランダムに決定され、各粒子間は連結しないような位相関係を持つ画像を生成しています。
多数の構造情報を持つ画像とPDとの対応関係(aは画像をbは画像に対応したPDをそれぞれ示している)
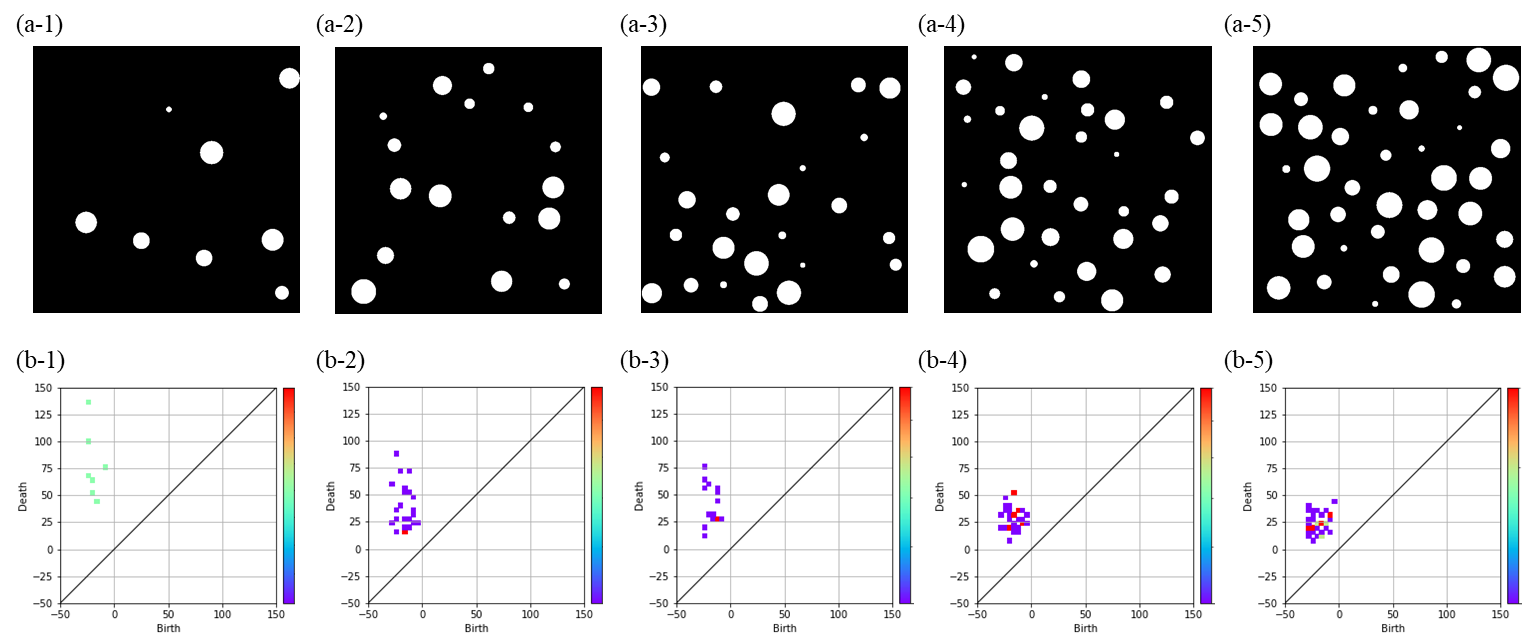
上図より以下のことを読み取ることが出来る。
- 構造の増加に伴いPD上のプロットの総数が増加している。(構造数-1のプロットが存在)
- birthは一定の範囲内に集中している
-> 構造の大きさは一定範囲内で生成されている - deathは正の領域のみに存在
-> 全ての構造は連結成分を持っておらず独立している - deathの分布範囲は構造数の増加に伴い小さくなっている
-> 構造数の増加に伴い、ある構造に対して最も短い境界間の距離が変化している
-> 構造の局所的な密度が変化
このように、多数の独立した構造では構造数や構造の局所的な密度といった情報を保存していることが分かる。
画像内の構造を回転させた場合
画像におけるPH解析で注意が必要な点として、構造の回転による情報の頑強性がある。数学的な理論に基づけば、PH解析は回転に対して頑強性が高い(回転しても情報が変わらない)が、画像においては回転によるノイズが発生してしまう。これは現実空間の距離が連続的な距離空間で定義されるのに対して、画像上では離散的な距離空間で定義されることによるものである。
離散化された距離空間の例
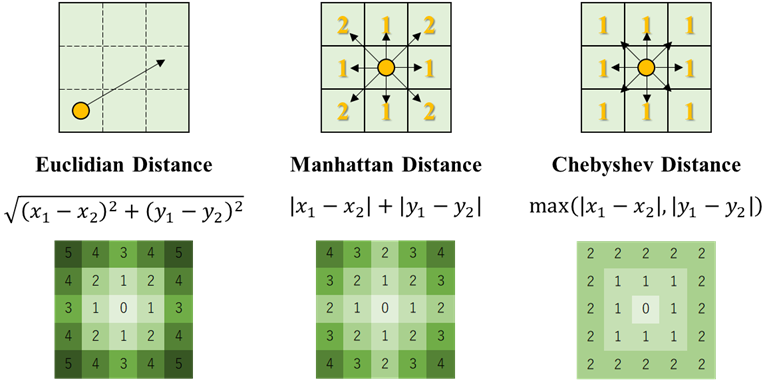
HomCloudでは距離空間を選択可能であるが、初期状態ではManhattan距離が選択されるため、これを前提として話を進めます。Manhattan距離によって定義された距離空間では、回転による影響が生じることが分かると思います。具体的に言えば、回転によって距離が1だったものが、2に変化します。これによって、現実空間では同じ構造(回転によって距離が変化しない)であったものが、画像内では構造に変化が生じてしまいます。この現象を理解する為にストライプ状の構造を回転させたものを次に示します。
ストライプ状構造を持つ画像とPDとの対応関係(aは水平方向にbは45°傾けた方向のストライプ状構造を示している。各情報は1は画像、2は画像から予想されるPD、3は算出されるPD、4は構造の境界に対する距離をそれぞれ示している。ここで、PDは簡単のため模式的な情報を記している。)

(a)の水平方向のストライプ状構造では、中央の太い構造を基準として、上下の構造がPD上にプロットされます。今回は上下ともに距離が等しく太さが同じデータであるので、PD上のプロットは1点に集中することが予想されます。実際にHomCloudの計算でも1点に集中したプロットが取得可能です。しかし、(b)の45°回転させた構造では、PH解析の回転による頑強性を考えれば同様なPDが取得可能であると予想されますが、実際には(b-3)にあるように対角性付近に大量のノイズを含む結果が算出されます。これは(b-4)にあるように、離散化された距離空間によってストライプ状構造の中心付近に多数の生成点(-5)が発生し、これがすぐに消滅することによってこの生成点の数だけ大量のノイズを対角線付近に生成してしまいます。ここで重要なのは、PH解析では本来、回転に対する頑強性を保有するという利点が画像では完全には保証できないという点です。これを解決する為にPDに対して重みづけ関数を用いた処理を行うことが有用となります。(詳細な議論に関しては[2][3]にあります。)HomCloudでは2つの重みづけ関数が用いられ、その一つである対角線からの距離に対する次式で定義される重みづけ関数を利用することでノイズを減少させることが可能です。
\omega \left ( b,d \right )=\textbf{arctan}\left ( C\left ( d-b \right )^{P} \right )
HomCloudを実際に利用する際には、ハイパーパラメータ (C,P) を設定することで対角線からの距離 (d-b) に関する重みづけを行うことが可能となっています。
ここで理解して頂きたいのは、ここまで連結成分を含まない構造として利用した円では回転に対して離散化の影響をほとんど受けませんが、例えば楕円形であったり正多角形のような通常連結成分を含まない(中心-境界間の距離が一定)構造であっても、回転に影響によってノイズを発生してしまうということです。画像におけるPH解析ではこういった事象が発生してしまうことも理解して解析を行うことが重要だと思います。
おわりに
本記事では実際に2値化画像に対するPH解析を行う際に注意してほしい点や、解析の補助とのある情報を記しました。上記のように実際に解析を行う際には様々な制約であったり、直感的な理解とは異なる部分もあったかと思います。個人的には今回のようにシンプルな画像を実際に生成してみて構造とPDの関係を直接観察することが解析において役立つと思いますのでご自身で画像生成をしてみて試してみてください。
今記載している以外にも画像解析に関して随時アップロードしていきたいと思いますので、参考にしてみてください。
参考文献
- [1] I. Obayashi et al, Persistence diagrams with linear machine learning models, J Appl. and Comput. Topology,421–449, 2018
- [2] H. Adams, Persistence Images: A Stable Vector Representation of Persistent Homology, J. Mach. Learn. Res. 18(8), 1–35, 2017
- [3] G. Kusano et al, Kernel method for persistence diagrams via kernel embedding and weight factor ,J. Mach. Learn. Res. 18(189), 1−41, 2018