概要
kivyのgraphicsクラスのメソッドで使い方が直感的に分からなかったものがあったので、思いだすようでかいておきたいと思います。説明するのは、color,ellipse,rectangle,meshです。
実行環境
次に実行環境を示します。
| Soft and Hard | バージョン |
|---|---|
| Ubuntu | 16.04 |
| Python | 2.7 |
| kivy | 1.10.0 |
また、Graphicsの公式ドキュメントはこちらです。
各メソッド
Color
後に描画される頂点の色の状態を設定するです。これは0と1の間の色を表しますが、続くキャンバス内の任意の頂点命令のテクスチャに
乗数として適用されます。テクスチャが設定されていない場合は頂点命令はColor命令の正確な色を取ります。例えば、Rectangleが均一な色(0.5, 0.5, 0.5, 1.0)
のテクスチャを持ち、先行Colorがrgba =rgba=(1, 0.5, 2, 1) の場合、実際の表示色は(0.5, 0.25, 1.0, 1.0) です。なぜならColor命令はすべての
rgbaコンポーネントに乗数として適用されるからです。 この場合は0〜1の範囲外の色成分は青色成分が目に2倍の強さになると結果を与えます。
引数を次に示します。
Parameters:
a:Added in 1.0.0
レッドコンポーネントは0~1です。
b:Added in 1.0.0
ブルーコンポーネントは0~1です。
g:Added in 1.0.0
グリーンコンポーネントは0~1です。
h:Added in 1.0.0
色相コンポーネントは0~1です。
hsv:Added in 1.0.0
HSVカラーは範囲が0~1の値が3つのリストと、1つのアルファを持ちます。
r:Added in 1.0.0
赤コンポーネントは0~1です
rgb:Added in 1.0.0
RGBカラーは範囲が0~1の値が3つのリストです。
rgba:Added in 1.0.0
RGBAカラーは範囲が0~1の値が4つのリストです。
s:Added in 1.0.0
彩度コンポーネントは0~1です。
v:Added in 1.0.0
値コンポーネントは0~1です。
ellipse
2次元の楕円を出力する命令です。引数を次に示します。
Parameters:
segments: int, デフォルト値は180
楕円を描くために必要なセグメントの数を定義します。 多くのセグメントがある場合は図はスムーズになります。
angle_start: int, デフォルトは 0です
円の部分の開始角度を度で指定します。
angle_end: int, デフォルトは 360です
円の部分の終了角度を度で指定します。
angle_end¶Added in 1.0.0
楕円の終了角度(単位:度)。デフォルトは360です。
angle_start¶Added in 1.0.0
楕円の開始角度(単位:度)。デフォルトは0です。
segments¶Added in 1.0.0
楕円のセグメント(分割)数を設定/取得するためのプロパティです。
rectangle
2次元の四角形を出力する命令です。引数を次に示します。
Parameters:
pos: list
四角形の位置を指定します。フォーマットは(x, y)です。
size: list
四角形の大きさを指定します。フォーマットは(width, height)です。
mesh
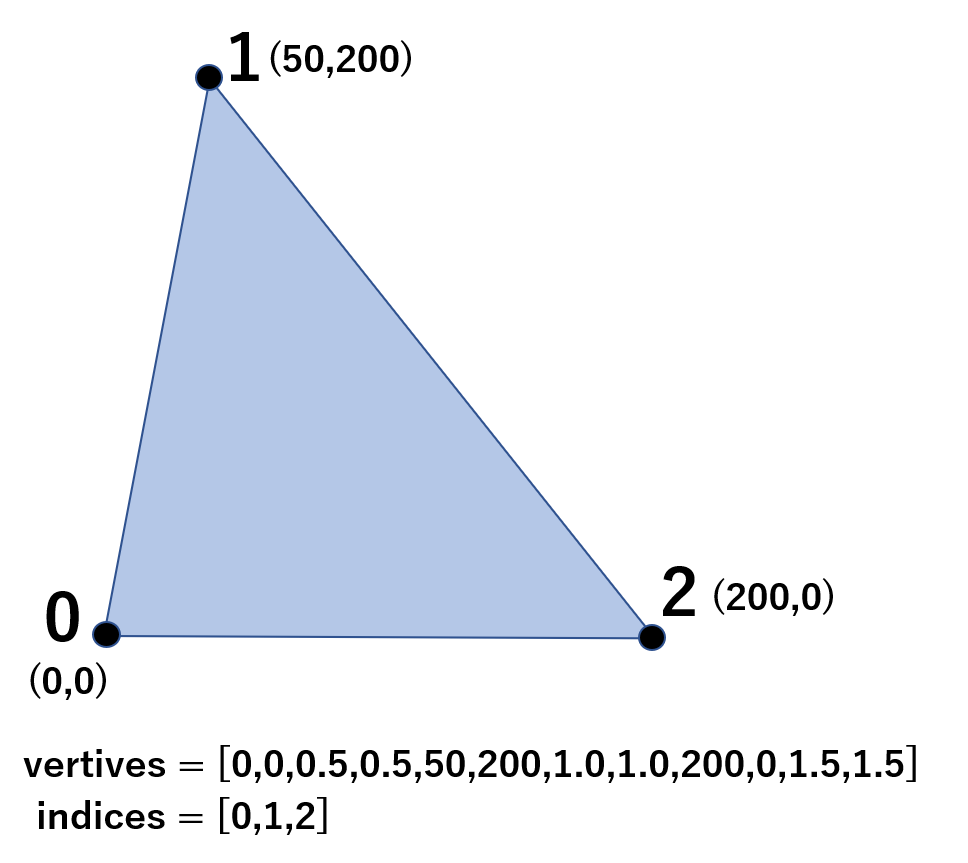
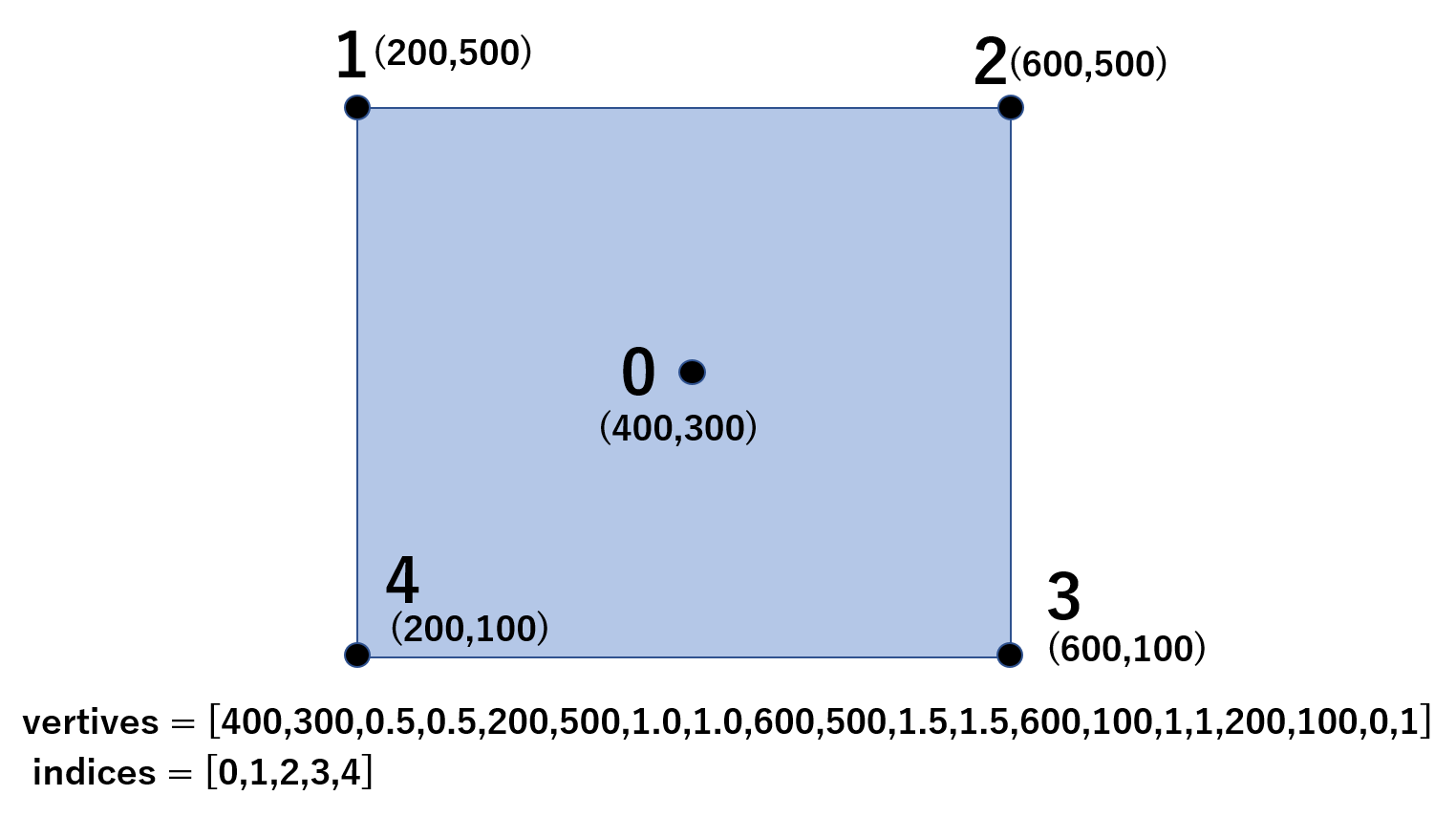
2次元のメッシュを出力する命令です。引数を次に示します。メッシュのindicesとverticesの関係は次のイメージで説明します。
Parameters:
indices: iterable
インデックスのリストのフォーマット (i1, i2, i3...)です。
vertices: list
メッシュの構築に使用されたx, y, u, v 座標のリスト。メッシュ命令では頂点のフォーマットを今すぐ変更できません。
つまり、x、y + 1つのテクスチャ座標だけです。
mode: str
インデックスの描画に使用されるVBOモードです。 ‘points’, ‘line_strip’, ‘line_loop’, ‘lines’, ‘triangles’,
‘triangle_strip’、’triangle_fan’ のいずれかになります。
fmt: list
verticeの形式は、デフォルトでは各頂点は2D座標(x,y)と2Dテクスチャ座標(U,V)によって記述されています。リストの各要素はtupleまたはリストの形式であるべきです。
また、三角形を描きたい場合は3つの頂点を追加します。次のようにしてインデックスリストを作成できます。
indices = [0, 1, 2]
三角形のイメージは次の通りです。
まとめ
3Dや2Dに関してあまり詳しくない為、meshのようなものにうーんとなってしまいました。うーんとなってしまっている人の助けになっていたら嬉しいです。