博報堂テクノロジーズの坂井です。
今回はマーケティングサイエンス系の業務でよく登場する「負の二項分布」に関するTipsを紹介します。
「負の二項分布」を扱うときに直面する壁
「負の二項分布(Negative Binomial Distribution; NBD)」は、マーケティングの実務でよく登場する確率分布です。生活者の商品の購買頻度や広告接触頻度を、パラメトリックな確率分布で表現する必要がある場合に有望な選択肢となります。
この負の二項分布を扱うときに実務者が直面する壁が、「文献や統計ライブラリによって、パラメータの取り方が違う」「そのパラメータの意味がわかりにくい」ことです。
- Wikipedia:https://ja.wikipedia.org/wiki/負の二項分布
- Excel: https://support.microsoft.com/ja-jp/office/negbinom-dist-関数-c8239f89-c2d0-45bd-b6af-172e570f8599
- Scipy: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.nbinom.html
- 高精度計算サイト: https://keisan.casio.jp/exec/user/1637663821
負の二項分布を扱いたいときにおそらくよく参照されるであろう文献・ライブラリを並べましたが、それぞれパラメータの定義や取り方が微妙に違います。またそのパラメータも、「それって購買頻度や広告接触頻度でいうとどういう意味なんだっけ?」と考え込んでしまうような、解釈の難しいパラメータを扱う必要があります。
負の二項分布を扱うマーケターはこれらパラメータを、手計算で慎重に変換しながら恐る恐る扱っているのが現状だと思います。
パラメータ変換早見表
本稿ではおすすめのパラメータの取り方として、森岡毅・今西聖貴著の「確率思考の戦略論」で用いられている $M$, $K$を用いたパラメータの取り方(以降、MK表記と呼ぶことにします)を取り上げます。
MK表記は、$M$ が負の二項分布の期待値、$K$が分布のバラツキ(厳密にはその逆の同質性)を表し、パラメータの解釈が明瞭なためおすすめです(補足1参照のこと)。
各文献・ライブラリのパラメータを、MK表記から変換する早見表がこちらです:
| パラメータをMK表記から変換 | 分布の期待値 | 分布の分散 | |
|---|---|---|---|
| MK表記 | $M=M$ $K=K$ |
$M$ | $M+M^2/K$ |
| Wikipedia: 負の二項分布 | $r=K$ $p=\frac{M}{M+K}$ |
$\frac{pr}{1-p}$ | $\frac{pr}{(1-p)^2}$ |
| scipy.stats.nbinom | $n=K$ $p=\frac{K}{M+K}$ |
$\frac{n(1-p)}{p}$ | $\frac{r(1-p)}{p^2}$ |
| Excel NEGBINOM.DIST 関数 | $成功数=K$ $成功率=\frac{K}{M+K}$ |
$\frac{成功数(1-成功率)}{成功率}$ | $\frac{成功数(1-成功率)}{成功率^2}$ |
早見表を見ると
- Wikipediaとscipyとでパラメータ $p$ の意味が逆になっている。
- scipyとExcelは表記が違うだけで実は同じパラメータの取り方をしている。
- パラメータと期待値や分散の関係は、MK表記が一番理解しやすそう
ということが言えると思います。
基本はMK表記で負の二項分布の理解を統一しつつ、この早見表を活用することで各文献やライブラリを上手に扱うことができます。
Scipyの場合
Scipyのnbinomモジュールを使う場合、次のような変換関数を挟むことで、MK表記で負の二項分布を扱うことができます:
from scipy.stats import nbinom
# MK表記のパラメータを受け取って scipy の nbinom を使えるようにする変換関数
def nbinom_MK(M, K):
n, p = K, K/(M+K)
rv = nbinom(n, p)
return rv
M, K = 5, 2.5
rv = nbinom_MK(M, K)
mean, var = rv.stats(moments='mv')
# (5.000000000000001, 15.000000000000004)
# 分布を描画
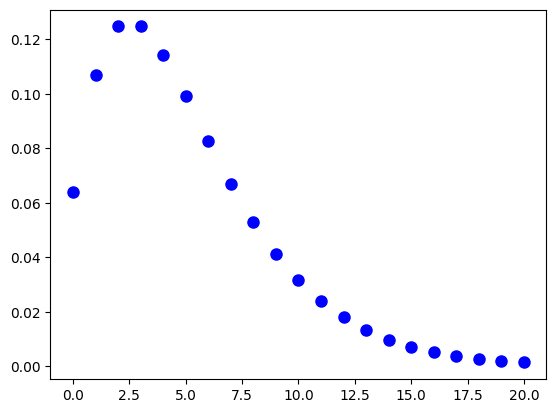
x = np.arange(0, 21)
plt.plot(x, rv.pmf(x), 'bo', ms=8, label='nbinom pmf')
plt.show()
補足1: M, Kの解釈
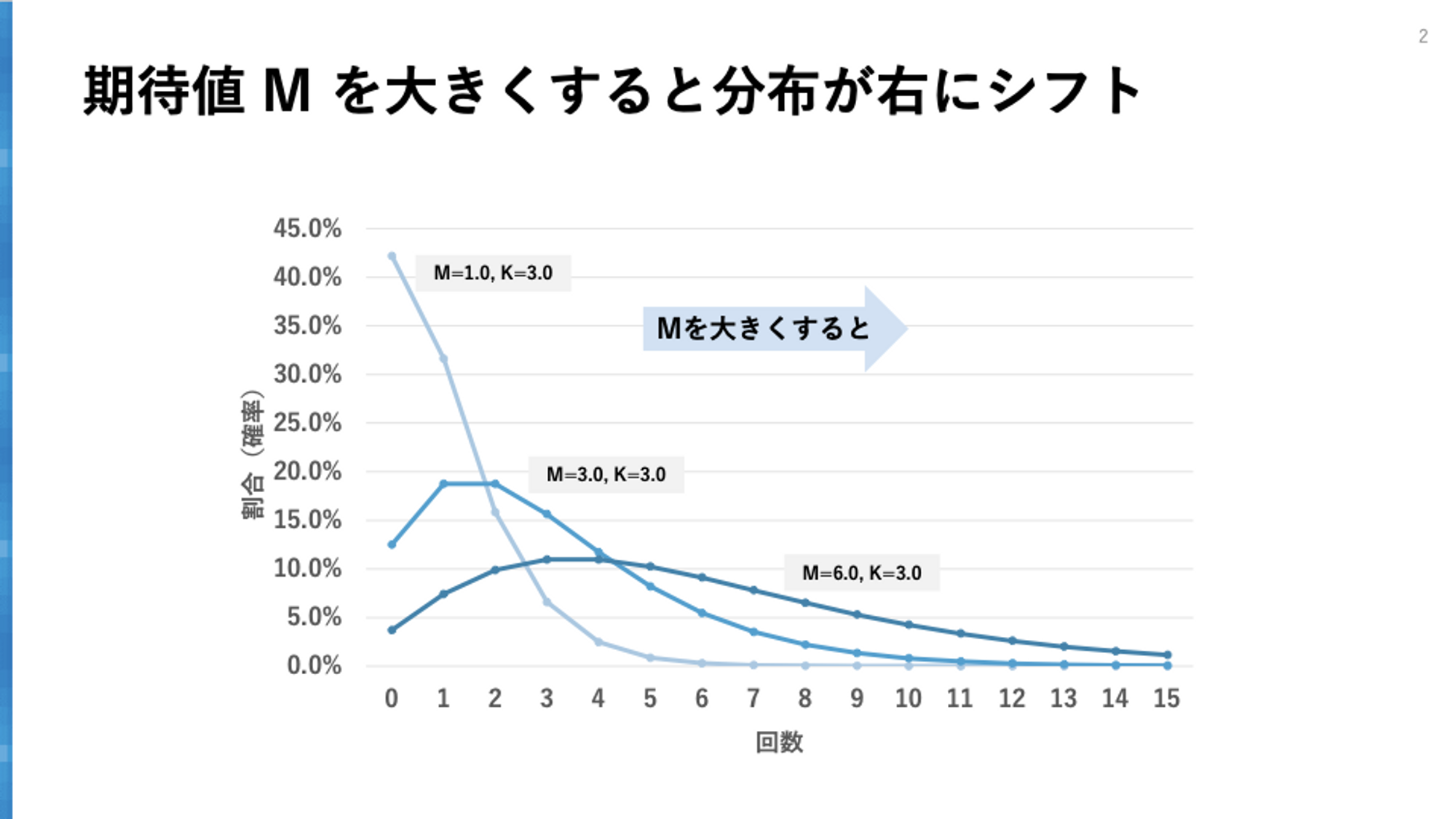
期待値パラメータ $M$ は、文字通り負の二項分布の期待値 $M$ で、分布の期待値・平均の場所を表します。$M$が大きいほど分布の中心は右にずれていきます。例えば購買頻度分布だとすると、$M$が大きいほど、集団としてたくさんの購買が行われることを意味しています。
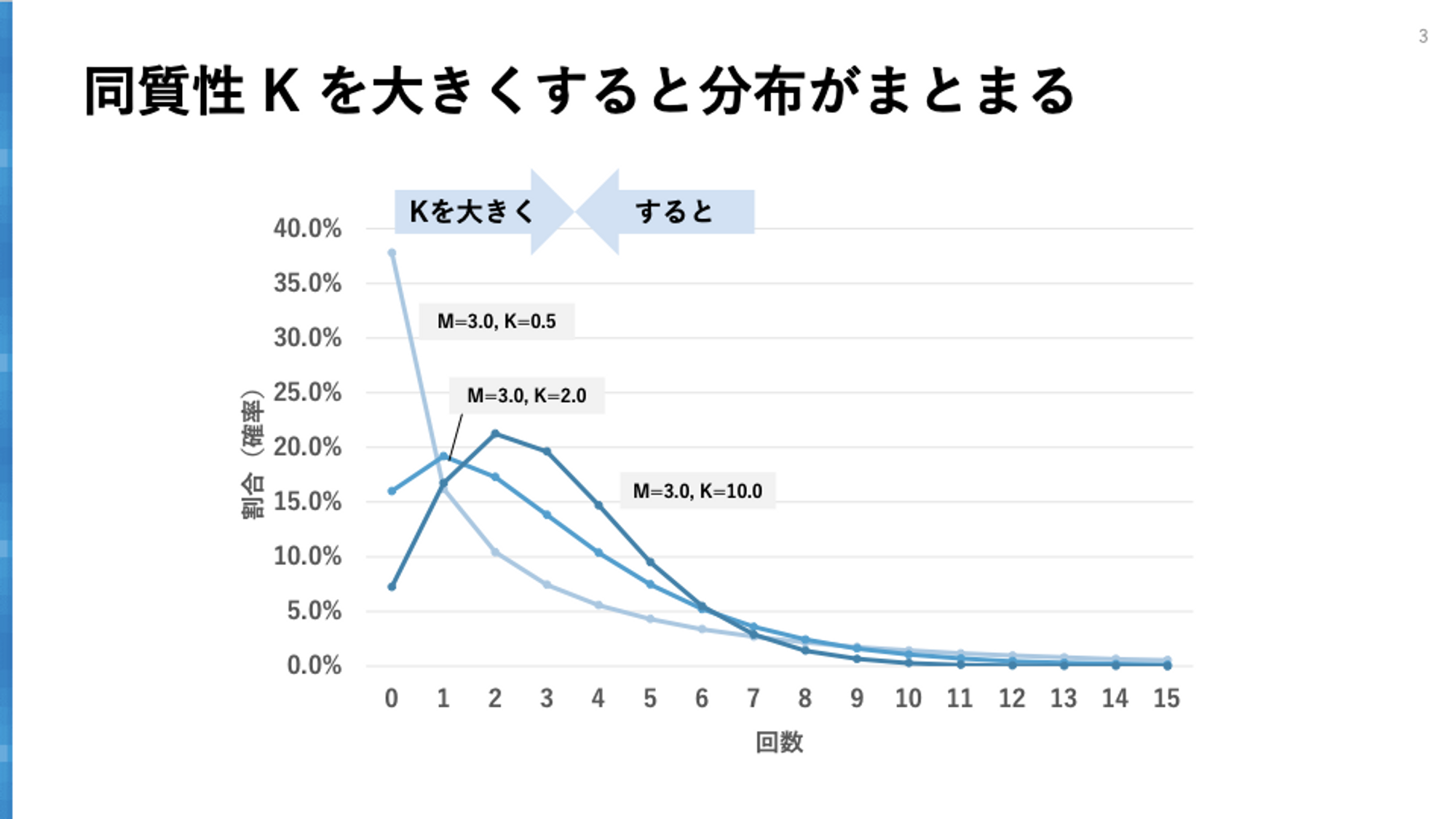
同質性パラメータ $K$ は、「分布のまとまり」を表します。$K$が大きいほど分散が小さく、分布はまとまっていきます。逆に$K$が小さいほど分布の広がりは大きくなります。購買頻度分布だとすると、$K$は集団の中の買いやすさの同質性を表し、$K$が大きいほどみんな同じような買い方をするため分布はまとまったものになっていきます。$K$が小さいと、集団の中の同質性は低く、よく買う人もいれば全然買わない人もいて分布が広がっていきます。
補足2: ExcelのNEGBINOM.DIST関数の注意点
ExcelのNEGBINOM.DIST関数は、成功数パラメータ($=K$)は整数以外の値を指定すると小数点以下が切り捨てられてしまう制約があります。しかし実務上は負の二項分布にデータを当てはめたい場合など、$K$は連続値の方が都合が良いケースが多いため、NEGBINOM.DIST関数が適していないときがあります
その場合はやや煩雑ですが、負の二項分布の確率関数をExcelのセルに関数で手打ちして無理やり再現する、ということを私はよくやります。

2022年にリリースされたLAMBDA関数をうまく使えばもう少しエレガントに書けるのかもしれません。