機械学習モデルの誤差を “四階層” に分解

博報堂テクノロジーズの坂井です。
業務で機械学習に取り組む際に「誤差」についてどう考えているかを共有します。

機械学習モデルの誤差を減らしたい

機械学習では完璧なモデルを学習するのは難しく、何らか誤差が残ってしまうのが普通です。

• 誤差は主に何が原因なのか
• どうしたら減らせる可能性があるのか

を実務家向けに系統的に整理してみました。

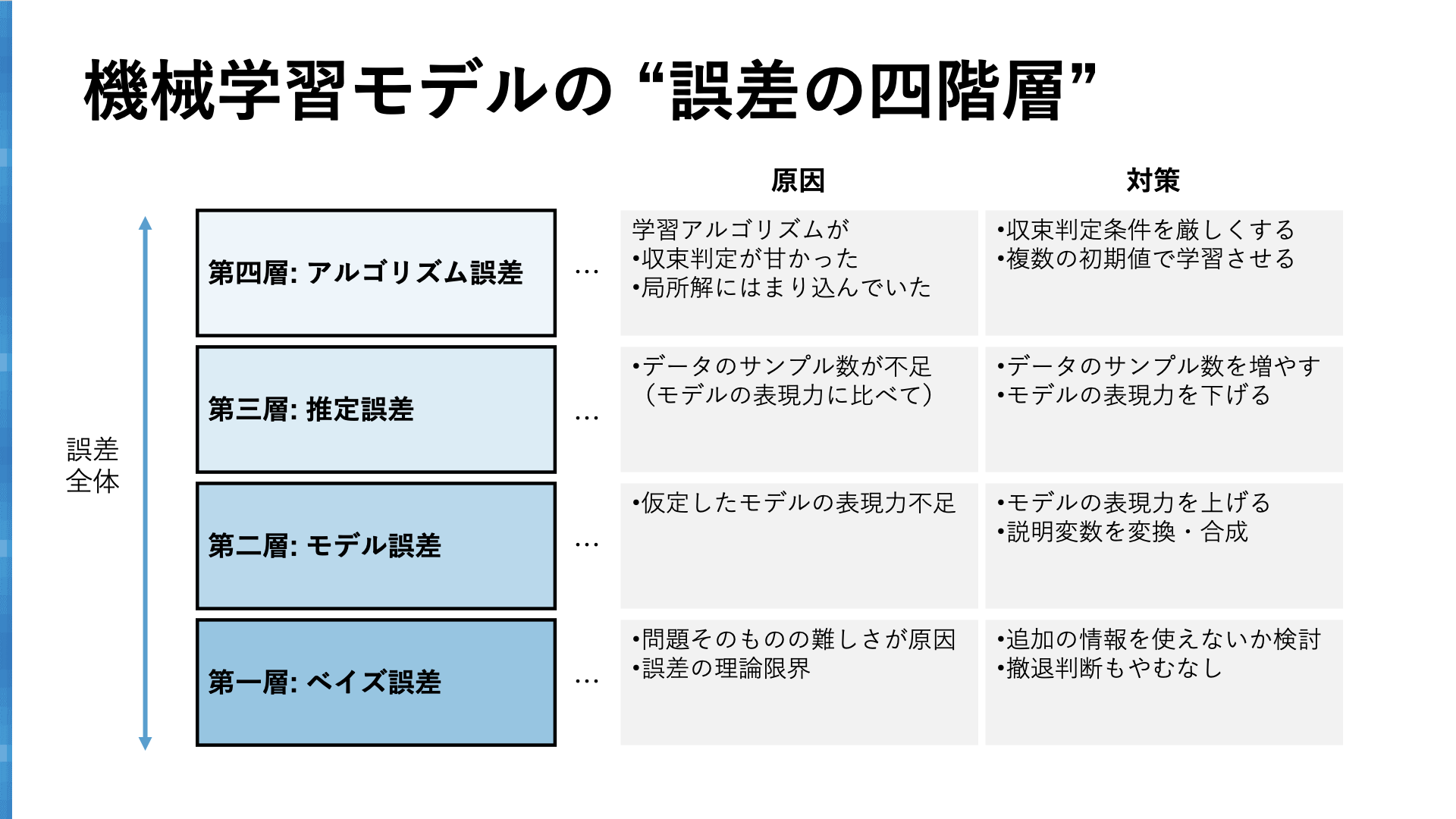
誤差を “四階層” に分解

機械学習モデルの誤差は、次の四階層に分解できます:

1. ベイズ誤差 - “誤差の理論限界”
2. モデル誤差 - “仮定したモデルの表現力が原因の誤差”
3. 推定誤差 - “データ量が原因の誤差”
4. アルゴリズム誤差 - “学習アルゴリズムが原因の誤差”

4つの層はそれぞれ、誤差を減らすための方策が違います。「このモデルにはどの誤差が一番多く乗っているんだろう」ということを推測しながら、筋の良い手立てを試していくことが有効です。

1~3階層のベイズ誤差・モデル誤差・推定誤差は一般的な概念です。詳細は金森敬文 "統計的学習理論"を参照ください。ただしモデル誤差は「近似誤差」と呼称されています。

4階層目のアルゴリズム誤差はあまり一般的ではありませんが、実務ではよく登場するため私が命名しました。もしかしたらもっと一般的な呼び方があるかもしません。

以下、各層をそれぞれ解説していきます。

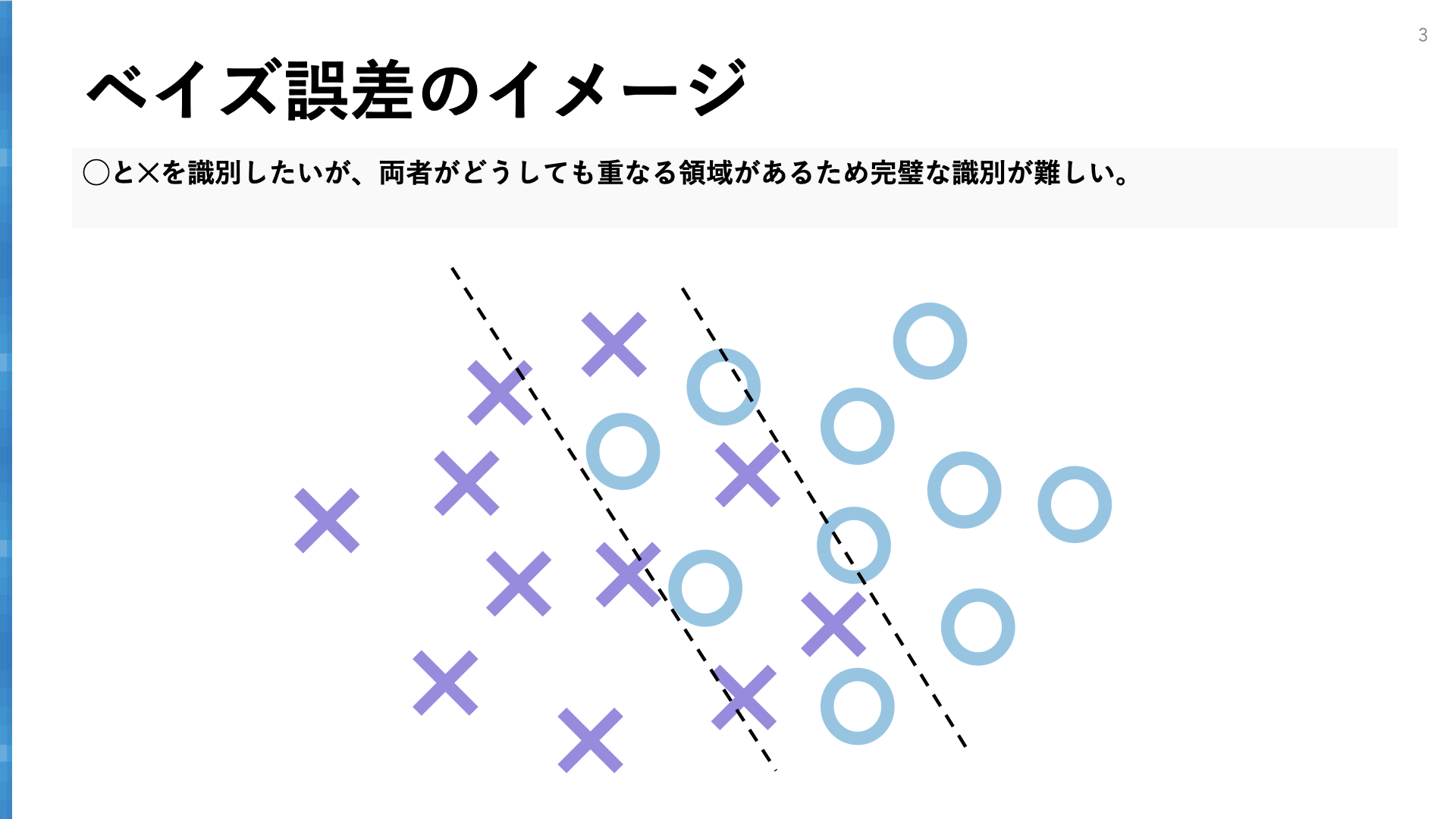
第一層: ベイズ誤差

第一層目の「ベイズ誤差」は、追加の情報がなければどうしたって減らすことができない誤差、つまり誤差の理論限界です。

シンプルな例として、「サイコロAとサイコロBを2つ投げて、Aの目からBの目を予測する」タスクを考えてみましょう。2つのサイコロの目は互いに独立ですから、どんなに優れたモデル・アルゴリズムを持ってきても、Bの目の予測は5/6は外れてしまいます。この誤差5/6=83%がベイズ誤差です。

ベイズ誤差を減らすためには、予測に使える情報を追加することを検討します。極端な話、もしサイコロBが静止する0.01秒前のサイコロBの姿勢や回転速度の情報を利用することができれば、サイコロBの目を予測できる可能性は大きく高まります。逆に追加情報も利用できない場合、絶対に減らせない誤差に立ち向かってしまっている可能性があります。その場合は早めに見切りをつけて撤退するのもひとつです。昨今の生成AIの隆盛によって機械学習への期待が非常に高まっていますが、そのタスクに固有のどうしても減らせない誤差があるのだということを認識しておくことはとても大切です。

目の前の機械学習タスクのベイズ誤差を正確に見積もることは残念ながら難しいのですが、上限を見積もるシンプルな方法があり、「人間が自らそのタスクをやってみること」です。もし人間が頑張ればある程度小さな誤差を達成できるのであれば、ベイズ誤差は人間の誤差より必ず小さくなります。画像識別や言語処理系のタスクは人間であれば簡単にこなせるタスクが多いでベイズ誤差も小さくなりますし、株価予測タスクなどは人間でもなかなか難しいタスクでベイズ誤差は大きいことが予想されます。

第二層: モデル誤差

第二層の「モデル誤差」は、仮定したモデルの自由度・表現力が不足していることが原因の誤差です。

たとえば線形識別モデルは、説明変数空間の中にまっすぐな境界線（面）を引くことで目的変数の正例と負例を予測するモデルです。もし図のように目的変数の正例と負例の境界が曲線を描いていたら、どんなにうまく学習しても、線形識別モデルでは誤差が残ってしまいます。このどうしても残ってしまう誤差がモデル誤差です。

モデル誤差を減らすには、

1. 仮定するモデルの自由度・表現力を上げること
2. 説明変数をうまく変換・合成すること

の2つが有効です。モデルの自由度を二次、三次と上げていけばモデルが真の境界面を表現できるようになっていきます。ただし後述の推定誤差は大きくなってしまうというトレードオフ関係に注意が必要です。

また説明変数の持ち方を変えてみたり、複数の説明変数と合成することによって、簡単なモデルのままでも誤差を小さくできる可能性もあります。たとえばその好例がマーケティングの分野での「年齢」変数です。特定の年齢に固有の行動・特性があるので、年齢変数はそのまま使うのではなく、10代・20代・30代などとフラグ化して扱う方がよいとされています。

第三層: 推定誤差

第三層の「推定誤差」は、データのサンプル数が不足していることが原因の誤差です。

また線形識別モデルを考えます。通常真の境界面が分かっていることはなく、データからうかがい知ることしかできません。誤差の観点でいうと、真の誤差を知ることはできず、モデルを手元にあるデータにあてはめた誤差しかわかりません。もしデータのサンプル数が少ないと、「手元のデータには充分当てはまっているのに、真の誤差は大きいままだった」という現象が起きます。これを「過学習」といいますが、この過学習で乗ってしまう誤差が推定誤差です。

推定誤差を減らすには、

1. データのサンプル数を増やしてみること
2. 仮定するモデルの自由度・表現力を下げること

の2つが有効です。通常、データのサンプル数を無限に増やすことができれば、推定誤差は限りなく0に近づけることができます。

また仮定するモデルの自由度を下げてシンプルなモデルにすることも有効です。しかしこれはモデル誤差を増やす可能性があるため、いい塩梅のモデルを選ぶ必要があります。このいい塩梅のモデルを選ぶことを「モデル選択」といい、有名な赤池情報量規準（AIC）やクロスバリデーションなどのモデル選択手法の活躍しどころになります。

第四層: アルゴリズム誤差

第四層の「アルゴリズム誤差」は、学習アルゴリズムがデータ上最適なモデルにうまくたどり着けなかったことが原因の誤差です。

機械学習モデルでは、データにもっともあてはまるモデルを探すために反復的な最適化アルゴリズムを利用します。もしアルゴリズムの反復の中で

• 収束判定が甘く、本当はまだまだ解を改善できるのにアルゴリズムが途中で終了してしまった
• データへの誤差関数が凸凹していて、局所解にはまり込んでしまった

などの事態が起きると、ベストの解を得ることができないため、その分追加で乗ってしまうのがこのアルゴリズム誤差です。

個人的には他の誤差に比べて一番もったいない・悔しいと感じてしまうので、一番最初になんとかしたい誤差です。アルゴリズム誤差を減らすには、

• 収束判定を厳しくしてみる（ただし学習時間が長くなってしまう）
• 複数の初期値から学習をさせて最も良い解を選ぶ

などの対策が有効です。

誤差の四階層の個別計測は難しい

誤差の四階層がわかったところで、できればそれを数値化できればよいのですが、私の知る限り四階層をそれぞれ直接計測することはできません。ホールドアウトデータがあれば誤差全体を推測することはできますが、四階層に個別に分解することはできません。試行錯誤を通して誤差を減らすことができて初めて、「そうかこの誤差が乗っていたのか」ということがおぼろげながらわかる程度です。

この誤差の四階層はもっぱら、モデルの精度改善のための引き出しとして、またチームで機械学習タスクに取り組む際の共通言語として役立ててもらえればと思います。

参考文献

• 金森敬文 "統計的学習理論"
  • 機械学習の誤差論について体系的に記されています。ベイズ誤差・モデル誤差（近似誤差）・推定誤差について記述があります。
• 鈴木大慈 "統計的学習理論チュートリアル: 基礎から応用まで"
  • 推定誤差についての理論的な解析のスライドです。
• Wikipedia “Bayse error rate”
  • ベイズ誤差についての解説です。