はじめに
この記事では基本的なアルゴリズムの一つである、ソートアルゴリズムを例にとってアニメーションを使って、アルゴリズムの計算量をみることを目的としています!
アルゴリズムを勉強していく中で、計算量という言葉を目にすることが多いと思います。
しかしながら、計算量について実際に、アルゴリズムごとでどの程度違うのか、ということは直感的に分かりにくいと思います。
そこで!
直感的に分かりやすいように、ソートアルゴリズムをこのようにアニメーションを使って可視化させてみたので、勉強の参考であったり、通勤中の暇つぶしなどに活用してみてください!
最初に計算量について解説するので、アニメーションだけ見てみたいという方は
実際に比較してみる
全体比較
をご覧ください!
弊社Nucoでは、他にも様々なお役立ち記事を公開しています。よかったら、Organizationのページも覗いてみてください。
また、Nucoでは一緒に働く仲間も募集しています!興味をお持ちいただける方は、こちらまで。
ソートアルゴリズムについて
ソートアルゴリズムとは、名前の通り「ソート(並び替え)」を行うアルゴリズムです。
例えば、[3, 7, 1, 4, 2, 5, 6]のような配列が入力データとして与えられた時に、ソートアルゴリズムを
実行することで、[1, 2, 3, 4, 5, 6, 7]のように整列されたデータを返してくれます。
計算量について
アルゴリズムの計算量は
・時間計算量
・空間計算量
に分類されます。
時間計算量は、処理にかかる時間を意味します。空間計算量とは、その処理が必要とする記憶容量を意味します。一般に計算量と言われたら時間計算量を指す場合が多く、この記事でも計算量は時間計算量のことを指します。
計算量(最良・平均・最悪)
(時間)計算量は
・最良計算量
・最悪計算量
・平均計算量
に分類することができます。
最良計算量は、処理時間の最小値を指します。しかし、最良計算量は限られた状況でしか起こり得ないため、アルゴリズムの性能を評価する際は、平均計算量と最悪計算量に注目します。
平均計算量は、そのアルゴリズムにおける平均的な処理時間を指し、最悪計算量は、そのアルゴリズムの最大となる処理時間を指します。
最悪計算量について
ソートアルゴリズムにおいて、多くのアルゴリズムでは、配列の初期状態やサイズにより計算量が左右されます。使用するアルゴリズムが不得意とする配列パターンであったり、単純にデータのサイズを大きくすることで、簡単に処理時間は膨大なものとなってしまいます。
また、シェルソートやクイックソートのように、アルゴリズム内での処理の仕方(間隔の取り方やピポットの設定)を適切に設定しないと、最悪計算量となってしまいます。
そのため、アルゴリズムを学ぶ上で、計算量に対する認識は重要なものになってきます。
ここまでつらつらと解説してみましたけど、見てみないとよくわからないと思うので、実際にどの程度変わってくるのかアニメーションを使ってみていきましょう!
実際に比較してみる
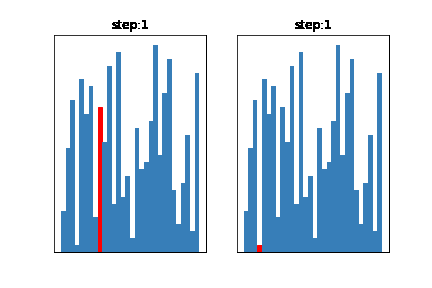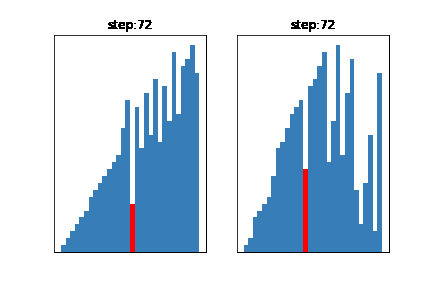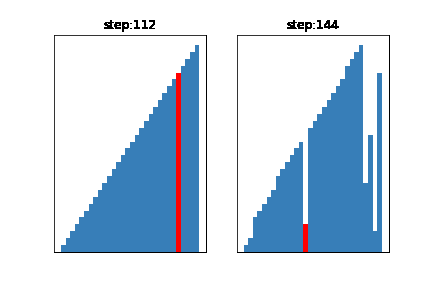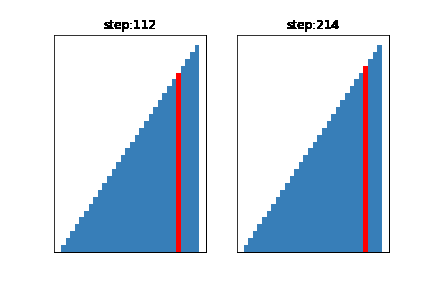
多くのアルゴリズムでは、苦手とする配列のパターンであったり、得意とする配列パターンが存在します。その配列の初期状態により、計算量が大きく左右されることがあります。基本的なソートアルゴリズムである、バブルソートは初期配列状態に大きく影響を受けるアルゴリズムです。そこで、バブルソートを例にとって初期の配列状態が計算量に与える影響をみてみましょう!
配列の初期状態で左右される場合
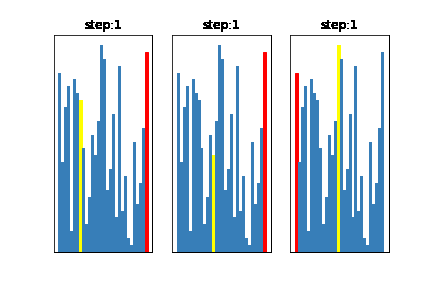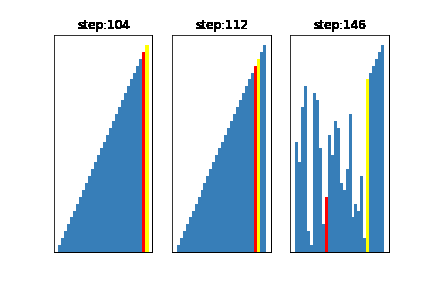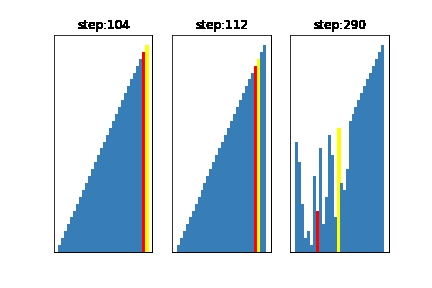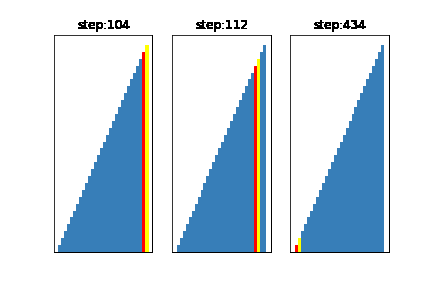
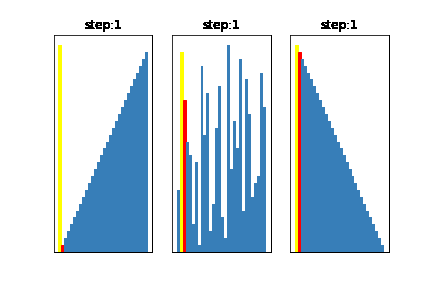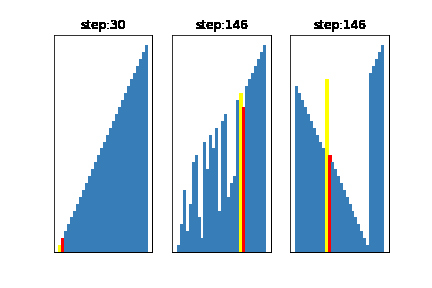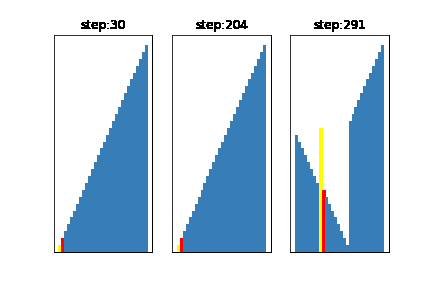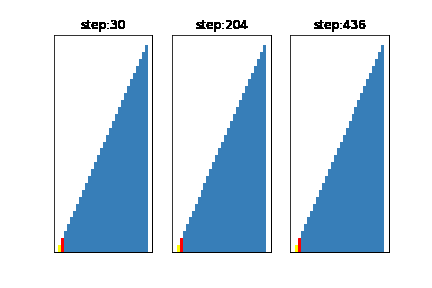
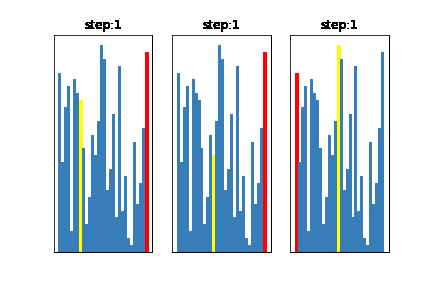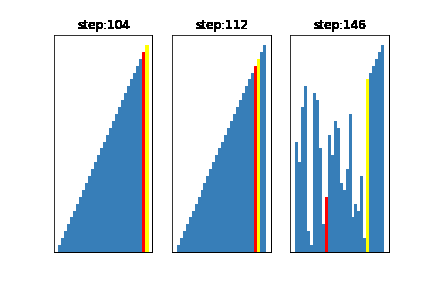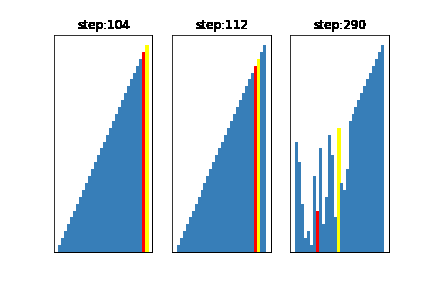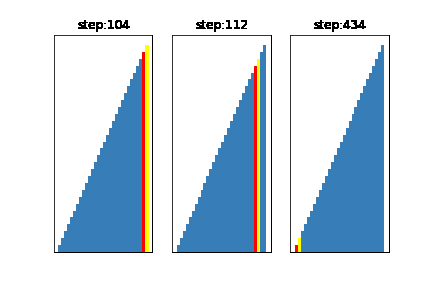
用意した初期配列状態は以下のようになります(データ数30)
左:ほとんどソート済み(最大値が一番左)のデータ
真ん中:ランダムに配置されたデータ
右:大きいものを左から並べたデータ
全然違いますね
左が最も速く処理が完了し、次に真ん中、最後が右という順番で処理が完了しており、同一のアルゴリズムでも初期配列状態により、処理速度に変化がでていることがわかります。
解説
バブルソートはソートアルゴリズムの中でも単純なアルゴリズムで、処理の内容としては
①隣合うデータの比較
②隣のデータが小さければ交換
これを繰り返すことにより並び替えを完了させます。
理解しやすいアルゴリズムですが、隣のデータいちいち確認し、交換を行うため、基本的に遅いアルゴリズムと言えます。また、一つ一つを確認するため、アニメーションの一番右のように、データが並び替えたい状態とは逆順に置かれていると、小さいデータ数でも処理に時間がかかってしまいます。
アルゴリズム内の処理の仕方により左右される場合
配列の初期状態や配列サイズによる影響の他にも、アルゴリズム内の処理の仕方が適切なものでないと、計算量が大きくなってしまう場合もあります。
どういうことかシェルソートとクイックソートを例にみてみましょう
シェルソート(間隔の取り方)
シェルソートは
①一定間隔でデータを取得し並び替え
②間隔を狭めてデータ取得し並び替え
これらを繰り返し行い、間隔が1になるまで繰り返し処理を行うことで、並び替えを完了させます。
シェルソートでは、この間隔の設定が重要で、不適切な間隔を設定すると計算量が増えてしまいます。
次の例では間隔を(データ数30)
左:$H_{n+1} = 3H_{n} + 1$の数列から得られる数における、要素数/9を超えない値の、大きいものから順に選ばれた間隔(一般的に良い結果が得られるとされる)
右:間隔を1にしたもの(挿入ソートと同じ状態)
で設定してみました
左と右でおおよそ2倍ほど差があることがわかると思います。
クイックソート(ピポットの取り方)
クイックソートは
①基準値(ピポット)を設定
②基準値よりも小さいグループと大きいグループに分割
これらを繰り返すことで並び替えを行います。
シェルソートは間隔でしたが、クイックソートはこの基準値の選び方が肝になってきます
今回は基準値の選び方を
左:グループの中からランダムに3つデータを取得し、その中央値を基準とする方法(一般的)
真ん中:グループからランダムにデータを1つ取得し、それを基準とする方法
右:基準値が常にそのグループの中の、最大値になるように選ぶ方法
となるように設定しました。
このように、基準値を不適切に選んでしまうと右のアニメーションのように、せっかく早いクイックソートを選んでるのに計算に時間がかかってしまうことがわかります
Pythonの組み込みソート(ティムソート)
ここまで読んだ方には、そもそもソートの計算量なんか気にしたことないし、ソートで時間かかったことないぞ、と考える方もいるかもしれません(自分がそうです)
それもそのはずで、Pythonに標準で搭載されているソート関数がとても優秀なソートアルゴリズムを採用しているため、みなさんはsort()を使えばその優秀なアルゴリズムを使って、並び替えを実行でき、ソートアルゴリズムについて、あまり考える必要がありません。
そんな優秀なアルゴリズムがティムソート(Tim Sort)です
ティムソートとは
詳しい解説は他の方に任せるのですが、簡単に説明するとティムソートは挿入ソートとマージソートのハイブリッド型のソートアルゴリズムです。ハイブリッド型にすることで、高速な処理を実現しています。
(Pythonの他にもSwift, Rustなどにも標準搭載されているらしい)
![]() https://ja.wikipedia.org/wiki/ティムソート
https://ja.wikipedia.org/wiki/ティムソート
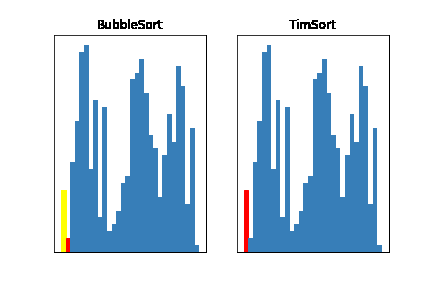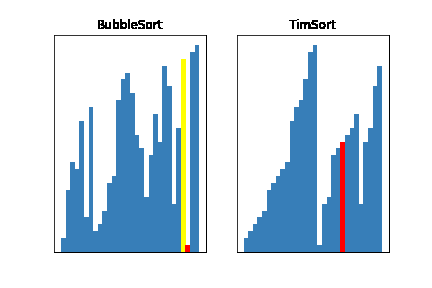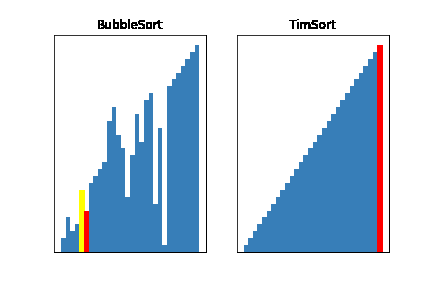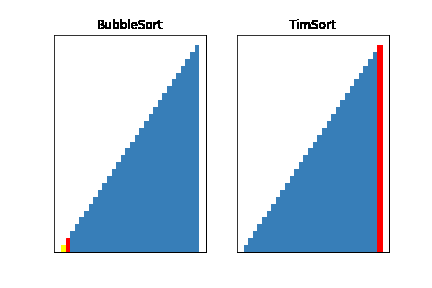
それではさっそく、ティムソートが実際にどれだけ速いのかみてみましょう!
今回はバブルソートと比較してみました
どうでしょう、だいぶ速いのがわかると思います!
全体比較
アニメーション比較
最後に全体比較ということで既に紹介した、バブルソート、シェルソート、クイックソート、ティムソート以外にも
・挿入ソート(InsertSort)
・選択ソート(SelectSort)
・マージソート(MergeSort)
・ヒープソート(HeapSort)
を加えた8種類で比較してみました!
おおまかな分類として、上段の左から3つのバブル、挿入、選択ソートは遅いアルゴリズムに分類されます
実際にこの3つは他5つのソートと比較して遅いですね。
残りの5つの中でみてみるとマージソートが遅く、シェルソート、クイックソート、ティムソート(Python標準)が速いことがわかります。
補足
一般的に、バブルソートよりも選択ソートの方が、処理時間でいうと速いアルゴリズムとなるのですが、このアニメーションだとバブルソートと選択ソートは同じ時間かかってるようにみえてしまいます。
では、何がバブルソートと選択ソートで違うのかというと、交換回数がバブルソートと選択ソートでは異なり、計算量に影響を与えます。
選択ソートでは、最小値(最大値)をデータ列から探して、直接先頭にいれるため、バブルソートよりも交換回数が少なくなります。
そのため、処理時間がバブルソートより選択ソートの方が速い結果となります。
計算量比較
最後に、今回使用したアルゴリズムの計算量を表にまとめておきます
計算量を記述するときは、オーダー記法と呼ばれる記法を用い、$O(n^2)$のように表されます(nはデータの個数)。これは、厳密な計算量を算出する式ではなく、あくまで大雑把にこれぐらいの計算量になるだろう、という目安を示す指標となります。
| 最悪計算量 | 平均計算量 | |
|---|---|---|
| バブルソート | $O(n^2)$ | $O(n^2)$ |
| 挿入ソート | $O(n^2)$ | $O(n^2)$ |
| 選択ソート | $O(n^2)$ | $O(n^2)$ |
| シェルソート | $O(n^2)$ * | $O(n^{1.5})$ * |
| マージソート | $O(n\log n)$ | $O(n\log n)$ |
| ヒープソート | $O(n\log n)$ | $O(n\log n)$ |
| クイックソート | $O(n^2)$ | $O(n\log n)$ |
| ティムソート(Python標準) | $O(n\log n)$ | $O(n\log n)$ |
*シェルソートの計算量は間隔に依存する(詳しくはWikipediaにあります)
![]() https://ja.wikipedia.org/wiki/シェルソート
https://ja.wikipedia.org/wiki/シェルソート
まとめ
いかがでしたでしょうか、今回はソートアルゴリズムを使って、アルゴリズムの計算量についてまとめてみました。
全体比較の結果からわかるように、ティムソートが速く、最悪計算量も$O(n\log n)$であるため、基本的に私たちはソート関数を用いればアルゴリズムを意識せずとも、速くソートを実行できることがわかります(ティムソートが標準的に搭載されている言語の場合)。
ソートアルゴリズムは現在においても、よりよいアルゴリズムを求めて研究は行われており、将来的にティムソートよりもさらに優秀なアルゴリズムが登場するかもしれません。
ソートは基本的な概念であるにも関わらず、いまだに研究が進められているのは興味深く、奥が深い世界なのだなと考えさせられますね
弊社Nucoでは、他にも様々なお役立ち記事を公開しています。よかったら、Organizationのページも覗いてみてください。
また、Nucoでは一緒に働く仲間も募集しています!興味をお持ちいただける方は、こちらまで。