-1. はじめに

この資料は現状、参考資料1の二番煎じとなっているので詳しく知りたい方は1をご覧になることをおすすめいたします。余裕ができたらわかりやすさの追求を行っていきます。

0. Camera Calibrationとは

Camera Calibrationとはカメラの内部パラメータの推定をすることを指します。この内部パラメータを用いることでカメラの画像平面上の点と実世界の点とを結びつけや位置・サイズ測定、歪みの除去などが可能となります。

この記事ではカメラキャリブレーションの理解を目標に書いていきます。

1. ピンホールカメラモデル

[2]より抜粋

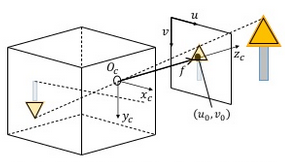
ある点Oを中心に環境を撮影する手法。ピンホールカメラモデルでは上下反対に撮影が行われるがそれでは扱いにくいため、仮想の画像面を配置し、それに写すように変換している(透視投影モデルへ変換)。
f: Oと画像面との距離
u, v:

2. 透視投影モデル

透視投影モデルに変換することで以下の式が得られる。ただし、Zは得られないため、X, Yを得ることはできない。

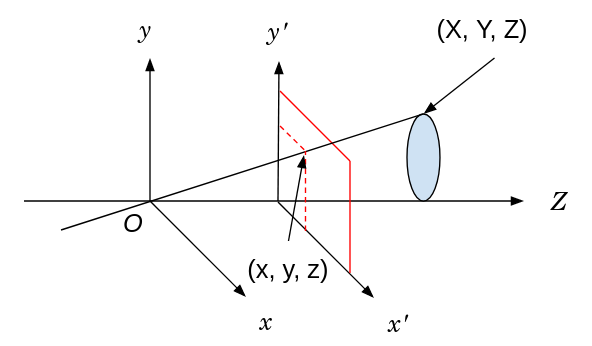
X = z \frac{X}{Z} \\
Y = z \frac{Y}{Z} \\
(z = f)

3. 同次座標の導入

同次座標系(homogeneous coordinates)は，射影幾何(projective geometry)に用いる、元の次元を１次元増やして座標系である．同次座標系の利点として，元のベクトルの回転(rotation)・並進(translation)・拡大縮小(scaling)・透視投影(perspecive projection)による変換を，各変換を表す行列の合成変換として一括に実施できる点が挙げられる．(3より抜粋)

(Ximage, Yimage): 画像座標系
(ox, oy): 画像中心
(Xcamera, Ycamera): カメラ座標系
(X, Y, Z): ワールド座標系
f: 焦点距離
(kx, ky): 画素の有効サイズ(≒画像の端)

ワールド座標系と理想なカメラの関係

\begin{pmatrix}
X_{camera} \\
Y_{camera} \\
1
\end{pmatrix} = 
\begin{pmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{pmatrix}
\begin{pmatrix}
X \\
Y \\
Z \\
1
\end{pmatrix}
\\

カメラ座標系と画像座標系の関係

\begin{pmatrix}
X_{image} \\
Y_{image} \\
1
\end{pmatrix} = 
\begin{pmatrix}
k_x & 0 & o_x \\
0 & k_y & o_y \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_{camera} \\
Y_{camera} \\
1
\end{pmatrix}
\\ -------------------------------- \\
X_{image} = k_xX_{camera} + o_x \\
Y_{image} = k_yX_{camera} + o_y \\
とも表現できる

この[[k_x 0 o_x] [0 k_y o_y] [0 0 1]]をA行列という

画像座標系からカメラ座標系へのベクトル

ベクトルと表現したのは一枚の画像から距離の推定は不可能なため

(X_{image} - o_x, Y_{image} - o_y, f)

ワールド座標系と画像座標系の関係

\begin{pmatrix}
X_{image} \\
Y_{image} \\
1
\end{pmatrix} = 
\begin{pmatrix}
k_x & 0 & o_x \\
0 & k_y & o_y \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 1 & 0 \\
\end{pmatrix}
\begin{pmatrix}
X \\
Y \\
Z \\
1
\end{pmatrix}
\\ = 
\begin{pmatrix}
fk_x & 0 & o_x & 0 \\
0 & fk_y & o_y & 0 \\
0 & 0 & 1 & 0 \\
\end{pmatrix}
\begin{pmatrix}
X \\
Y \\
Z \\
1
\end{pmatrix}

この[[fk_x 0 ~ 1 0]]をK行列という

4. カメラのパラメータ

内部パラメータ

内部パラメータとはカメラのレンズや曲面鏡などによって生じる特性を表したものです。

K行列 = 
\begin{pmatrix}
fk_x & 0 & o_x & 0 \\
0 & fk_y & o_y & 0 \\
0 & 0 & 1 & 0 \\
\end{pmatrix}

K行列はカメラの内部パラメータを指します。内部パラメータはカメラの姿勢には影響されません。

外部パラメータ

外部パラメータとはワールド座標系でのカメラの位置と姿勢を表したものです。外部パラメータを用いることでカメラの座標をワールド座標系へ変換することが可能です。
外部パラメータはワールド座標系の位置Tと姿勢Rによって決定されます。

\begin{pmatrix}
X_{camera} \\
Y_{camera} \\
Z_{camera} \\
\end{pmatrix}
=
\begin{pmatrix}
r_{11} & r_{12} & r_{13} & t_1 \\
r_{21} & r_{22} & r_{23} & t_2 \\
r_{31} & r_{32} & r_{33} & t_3 \\
\end{pmatrix}

\begin{pmatrix}
X_{world} \\
Y_{world} \\
Z_{world} \\
1 \\
\end{pmatrix}
\\
もしくは
\\
\begin{pmatrix}
X_{camera} \\
Y_{camera} \\
Z_{camera} \\
\end{pmatrix}
=
\begin{pmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33} \\
\end{pmatrix}

\begin{pmatrix}
X_{world} \\
Y_{world} \\
Z_{world} \\
\end{pmatrix}
+
\begin{pmatrix}
t_1 \\
t_2 \\
t_3 \\
\end{pmatrix}

上式の[[r_11 r_12 ~ r_33 t3]] が外部パラメータとなります。また、下式の [[r_11 r_12 ~ r32 r33]]を回転行列R,
[t_1 t_2 t_3] を並進ベクトルtと言います。上の式と下の式の違いは同次座標系を導入したかしないかの違いとなっています。

カメラ座標系からワールド座標系への変換は以下式より行なえます。

\begin{pmatrix}
X_{world} \\
Y_{world} \\
Z_{world} \\
\end{pmatrix}
=
R^T
(
\begin{pmatrix}
X_{camera} \\
Y_{camera} \\
Z_{camera} \\
\end{pmatrix}
- t
)

参考資料

視覚の幾何学
http://web.wakayama-u.ac.jp/~wuhy/CV09.pdf
SLAMの概要と画像を用いた3Dモデリングの基礎
https://www.slideshare.net/KenSakurada/slam3d
同次座標系 | CVMLエキスパートガイド
https://cvml-expertguide.net/2019/09/16/homogeneous-coordinates/
NO MORE! 車輪の再発明
https://mem-archive.com/2018/02/17/post-74/
https://mem-archive.com/2018/10/28/post-962/

カメラパラメータ・座標変換