-1. はじめに
この資料は現状、参考資料1の二番煎じとなっているので詳しく知りたい方は1をご覧になることをおすすめいたします。余裕ができたらわかりやすさの追求を行っていきます。
0. 2枚の画像からの深度推定
ステレオカメラでは、2枚の画像の差から深度推定を行うことができます。今回はそのやり方を詳細に述べます。
1. 深度推定概要
光軸を平行に
光軸(レンズ、球面鏡の中心を結んだもの)が並行でない場合、平行になるように変換する必要があります。ステレオカメラでは左のカメラに光軸を合わせるのが一般的らしいです。
多分ですが、以下式でなくとも座標系を共通にできれば良いので、計算一回増えますが、両方を世界座標系にしてもできるかも?
変換前座標系: (X, Y, Z)
変換後座標系: (X', Y', Z')
X' = T, Y' = X' * Z, Z' = X' * Y'
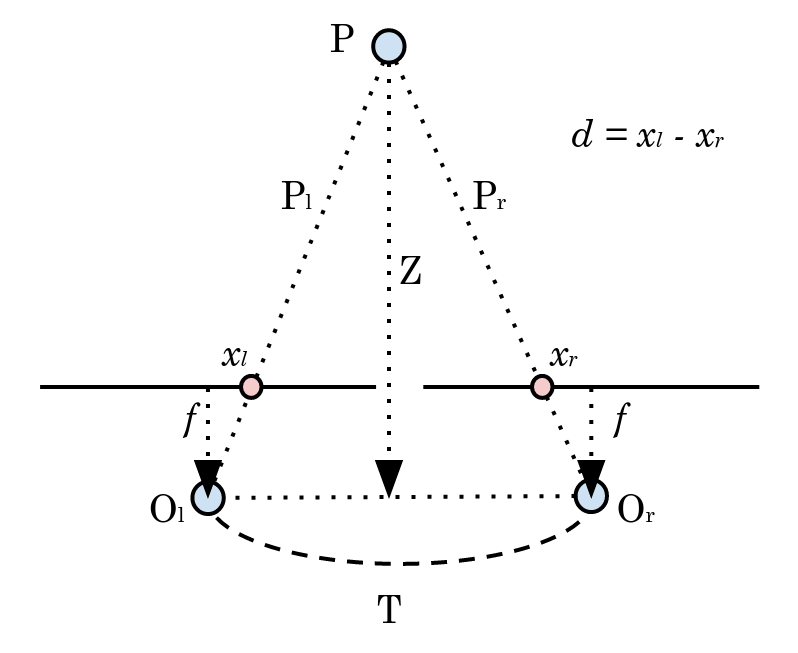
深度推定公式
Z = f\frac{T}{d} \\
\\
x_l, x_r: 点の画像上での座標 \\
f: 焦点距離 \\
T: 1枚目と2枚目の世界座標での距離( O_r - O_l = T ) \\
2.対応点の探索のためのエピポーラ幾何
2枚の画像から対応点を見つけるためには対応点を探索する必要があります。その際、画像上を愚直に探索してはとても時間がかかってしまいます。そこでエピポーラ幾何なるものをを利用します。
エピポーラ幾何とは、2つのカメラで同じ三次元空間を撮影した際に生じる幾何のことです。
ここから、エピポーラ幾何の理解のために必要な単語を紹介します。
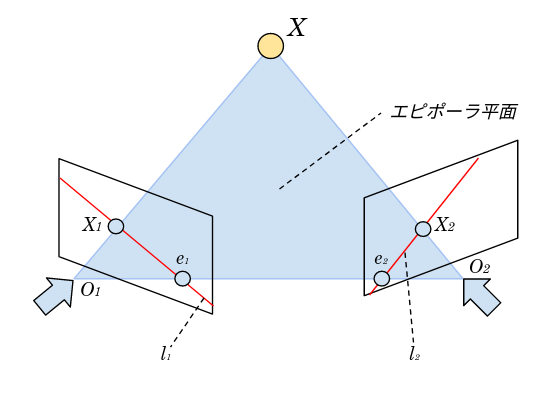
エピポーラ平面
カメラ $ O_1 $, カメラ $ O_2 $ 点 $ X $ の3点を通る平面
エピポーラ線
エピポーラ平面と画像平面が交わる直線で、上記画像の赤線($l_1$, $l_2$)です。
エピポール
2枚の画像の全ての対応点のエピポーラ線は必ず1点で交わります。それがエピポール($e_1$$e_2$)となります。これはもう一方の画像のカメラ中心を自身の画像に投影したものとなります。
基礎行列(Fundamental Matrix)
3*3行列で、カメラの内部・外部情報を含んでいます。この行列があると以下のことができます。
- 別の画像上の点を別の画像上のエピポーラ線にマッピングできる
- カメラ運動の推定
基本行列(Essential Matrix)
3*3行列で、カメラ外部情報を含んでいます。
カメラ内部行列Kと基礎行列Fを用いて、$ E=K_2FK_1 $ と変換できます。
2.1. 基礎行列Fの導出
$ x_1 $ と $ x_2 $ が対応点である場合、全ての対応点 $ x_1 $, $ x_2 $で以下の関係が成り立ちます。
x^T_2Fx_1 = 0 \\
F: 基礎行列 \\
x_1, x_2: 画像座標系での対応点の座標を同次座標系で表したベクトル
この式は、2つの画像の対応点に拘束関係があることを示します。これをエピポーラ拘束式といいます。これは画像1の点が画像2上のどこに写っているかを決定(=拘束)できます。
この図に例えると 左画像の$X_1$と基礎行列Fから右画像の $ l_2 $が求められるといった感じです。
F値の導出には次のようなアルゴリズムがあります。
- 8点アルゴリズム
- 代数的なコスト最小化
- 観測点と推定点との距離の誤差の最小化(Good Standard Algorithm)
これらはどれも最小二乗法などの繰り返し計算を用いています。
まとめ
- 深度推定は2枚の画像の対応点と焦点距離(内部パラメータ)、そして姿勢の移動量があれば求めることができる
- 対応点の探索のためにエピポーラ幾何を導入すると対応点が存在する線であるエピポーラ線が求められ、計算が早くできる
参考資料
- 視覚の幾何学 http://web.wakayama-u.ac.jp/~wuhy/CV10.pdf
- 【コンピュータビジョン】ネコと学ぶエピポーラ幾何
https://qiita.com/ykoga/items/14300e8cdf5aa7bd8d31