はじめに
記事は前半と後半に分かれています.
前半のこの記事では,暗号理論の基本的な話をざっっっくりと説明します.
それから最強の暗号の一角である格子暗号の背景をこれまたざっっくり話します.
後半の記事では,格子暗号のアルゴリズムを少し詳しく見ていきます.
ここでは幾何的な意味も考えながら直観的なイメージを持ってもらうことがゴールです.
簡単のために多少曖昧なところがあったり微妙に語弊があるところもありますが目を瞑ってください.
暗号とは
世の中には人に知られたくない情報というものは山ほどあります.
その情報を第三者が見ても読めないようにする技術を暗号(cryptography)といいます.
知られたくない情報を平文(plaintext)といい,平文に暗号を施したものを暗号文(ciphertext)といいます.
また,平文を暗号文にすることを暗号化(encryption)といい,暗号文を元の平文に戻すことを復号(decryption)といいます.
暗号化と復号をするときにはそれぞれ鍵(key)というものが必要です.
普通のドアなどでは,鍵と言えば1つの鍵で開けたり閉めたりしますが,暗号化の鍵と復号の鍵は同じとは限りません.
暗号化の鍵(暗号化鍵)と復号の鍵(復号鍵)が同じである暗号を共通鍵暗号といい,違うときは公開鍵暗号といいます.
記事の後編では公開鍵暗号を扱うので公開鍵暗号はおさえておいてください.
共通鍵暗号はぶっちゃけ飛ばしてもいいですが,公開鍵暗号の理解の助けにはなると思います.
共通鍵暗号
簡単な例で共通鍵暗号を説明します.
ここでは最も簡単な共通鍵暗号であるCaesar暗号(シーザー暗号)を紹介します.
Caesar暗号
シチュエーションとして,AliceがBobに"I love you"と告白したいとします.
しかし恥ずかしがり屋のAliceは誰にもBobへの告白を知られたくないです.
そこで告白の文の各アルファベットをアルファベット順に9文字分ずらすことにしました.
ただし,'z'まできたら次は'a'に循環させます.
(この9文字分というのが鍵で,ずらす文字数はなんでもOKです)
すると次のようになります.
I love you $\to$ R uxen hxd
(簡単のため,空白は暗号化していません)
ここでは,"I love you"が平文,"R uxen hxd"が暗号文です.
"love"をずらす様子だけ図$1$に示しておきます.
'v'をずらすときは'z'$\to$'a'と循環しています.
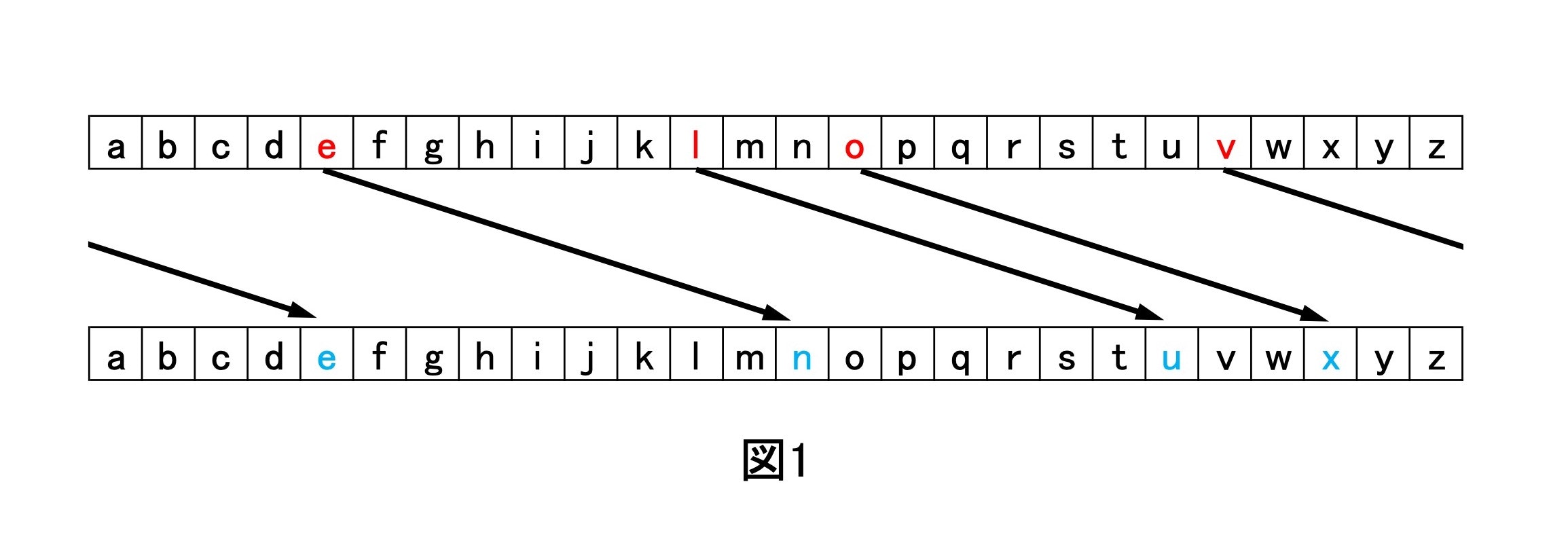
これで他人が見てもBobへの告白とわからなくなりましたね.
しかしBobでさえもこれを見たら意味のわからない文字列です.
そこでBobは送られてきた暗号文をアルファベット逆順に9文字分ずらします.
R uxen hxd $\to$ I love you
これでBobはAliceからの告白を受け取ることができました.
ここで,暗号鍵はAliceが平文をずらすときに使った「9文字分」というものです.
復号鍵はBobが暗号文を戻すときに使った「9文字分」です.
暗号化鍵と復号鍵が一致しているので共通鍵暗号という名前がついています.
共通鍵暗号の弱点
しかし,共通鍵暗号には弱点があります.
それは,Bobはどうやって「9文字分」という鍵を手に入れるかです.
一番初めに思いつくのは,Aliceが事前にBobに「9文字分」という鍵を送っておくことです.
しかし安全にAliceがBobに鍵を渡すやり方が存在するなら,そもそもそのやり方で平文を送ればええやんって話ですよね.
このように送信者が受信者とどうやって鍵を共有するかという問題を鍵配送問題とかいったりします.
この鍵配送問題を解決するのが公開鍵暗号です.
公開鍵暗号
次に公開鍵暗号です.
こちらは簡単な例が思いつかないので一般的にやっちゃいます.
公開鍵暗号
AliceはBobに平文$m$を送りたいとします.
送信者がAliceで,受信者がBobということを常に意識してください.
複雑な話が続くのでこれを意識していないとわけがわからなくなります.
まずは,Bobは秘密鍵(secret key) $s$と公開鍵(public key) $p$を作ります.
(共通鍵暗号とは違い,受信者が鍵を作ります)
その名の通り,秘密鍵はBobが自分の手元に秘密においておく鍵,公開鍵はWEB上などで公開する(誰に知られてもOK)ものです.
制約として,公開鍵で暗号化した暗号文を秘密鍵で復号できなければならないというものがあります.
状況としては下図$1$.

次にAliceは平文$m$をBobの公開鍵$p$で暗号化したもの(暗号文$c$)をBobに送ります(下図$2$)
ここで,暗号文$c$を誰でも盗聴できるという仮定をして暗号文を公開情報としてみました.
(よくわからなかったら気にしなくても大丈夫です)
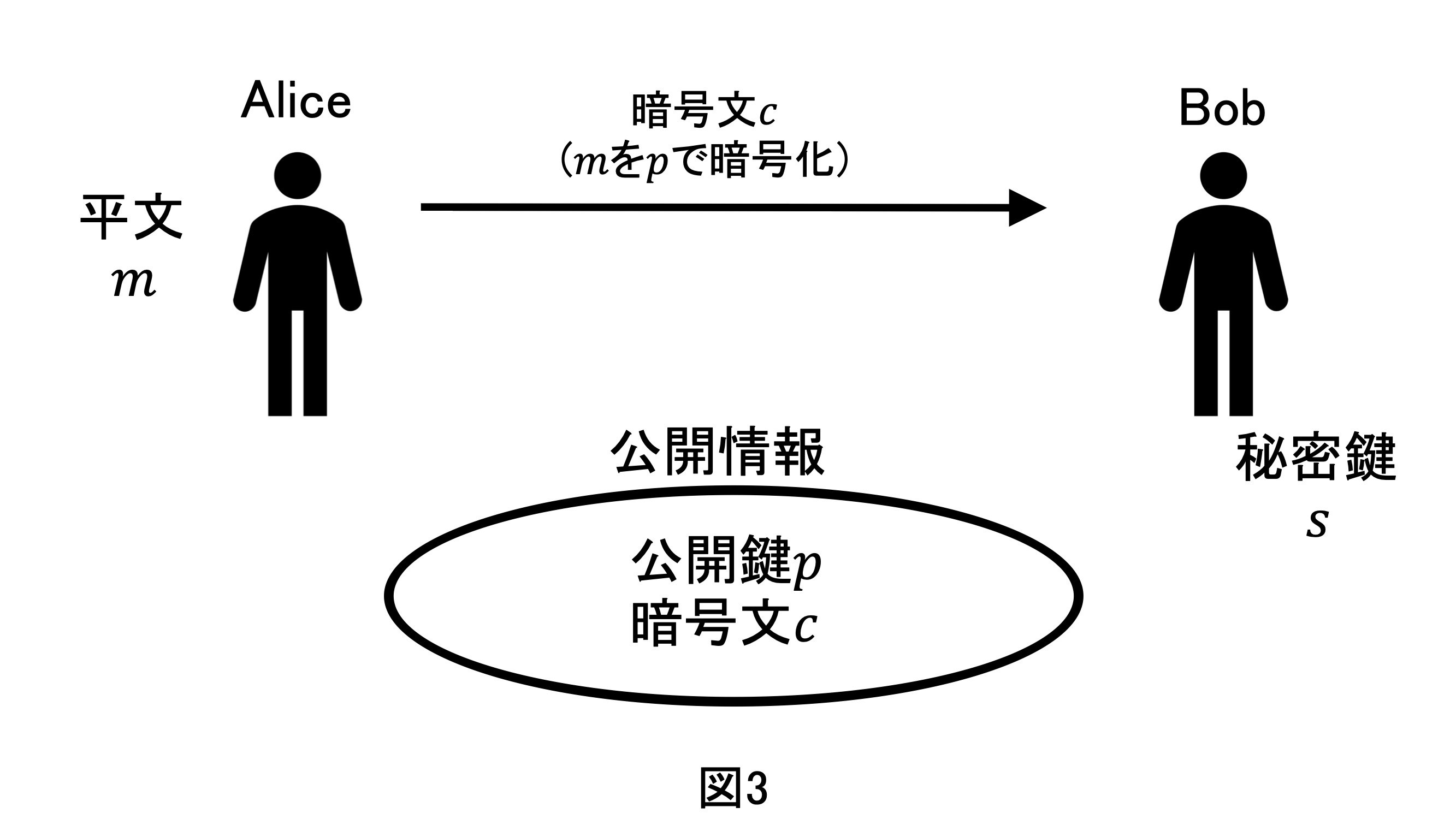
最後に,Bobは暗号文$c$を自分の秘密鍵で復号して元の平文$m$を得ます.
細かい話
色々不思議な点があるかと思います.
・メリットは?
$\to$ 共通鍵暗号のときの,鍵をどうやって共有するかという問題(鍵配送問題)が解決しています.
・誰でも暗号化できてええんか?
$\to$ 大丈夫です.誰が暗号化しようと復号できるのはBobだけです.
・公開鍵暗号だけ使えばいいのでは
$\to$ 実はそれは違います.公開鍵暗号は共通鍵暗号よりも遥かに処理に時間がかかるという特徴があります.実際はハイブリッド暗号という両者をいいかんじに混ぜた技術が使われます.
自分が初め不思議だったのはこのあたりです.
それぞれ一長一短あるということですね.
以上が共通鍵暗号と公開鍵暗号の概要になります.
それではいよいよメインテーマである耐量子暗号の話に移ります.
耐量子暗号
暗号の安全性
まずは耐量子暗号が必要である理由から話します.
上のCaesar暗号を思い出してください.
"R uxen hxd"に対する鍵は$0$~$25$の$26$個しかありません.
なぜなら,アルファベットが$26$文字周期であるためです.
例えばアルファベットを$3$文字分ずらす操作と$29$文字分ずらす操作は実質同じです.
つまり暗号文を$26$通りの方法でアルファベット逆順にずらせばその中に平文はあり,しかも意味の通る文章はかなり限られてきそうです.
このようにありうる場合を全て試すことを全探索といいます.
上の例でのAliceの告白の暗号文を全探索して復号してみましょう.
key= 0, text= "R uxen hxd"
key= 1, text= "Q twdm gwc"
key= 2, text= "P svcl fvb"
key= 3, text= "O rubk eua"
key= 4, text= "N qtaj dtz"
key= 5, text= "M pszi csy"
key= 6, text= "L oryh brx"
key= 7, text= "K nqxg aqw"
key= 8, text= "J mpwf zpv"
key= 9, text= "I love you"
key= 10, text= "H knud xnt"
key= 11, text= "G jmtc wms"
key= 12, text= "F ilsb vlr"
key= 13, text= "E hkra ukq"
key= 14, text= "D gjqz tjp"
key= 15, text= "C fipy sio"
key= 16, text= "B ehox rhn"
key= 17, text= "A dgnw qgm"
key= 18, text= "Z cfmv pfl"
key= 19, text= "Y belu oek"
key= 20, text= "X adkt ndj"
key= 21, text= "W zcjs mci"
key= 22, text= "V ybir lbh"
key= 23, text= "U xahq kag"
key= 24, text= "T wzgp jzf"
key= 25, text= "S vyfo iye"
全通りの復号結果を見てみると,key$=9$のときしか文章が成り立っていないです(英語なら)
つまり,Caesar暗号は暗号としては強くないと言えそうです.
ちなみに,全探索で平文を得ようとすることを総当たり攻撃や,ブルートフォースアタック(Brute-force attack)といいます.
ほとんどの暗号は全探索により解読が可能ですが,場合によってはとてつもない時間がかかったりします.
例えば$0$~$9$の$10$通りの数字で構成された$20$桁のパスワードを当てることを考えると,全探索をしようと思ったら$10^{20}$のパターンを試さないといけません.
先ほどの$26$通りとは天と地ほどの差がありますね.
耐量子暗号
このように解読にかかる時間によって暗号の安全性は保たれています.
しかし世の中には量子コンピュータというものが開発されつつあります.
量子コンピュータを用いれば,現在普通のコンピュータではとてつもなく時間がかかる処理も効率的に処理できることがあります.
この量子コンピュータを使っても解読にとてつもなく時間がかかることが証明できればその暗号はかなり強いと言えそうですね.
量子コンピュータでも効率的に解けない暗号のことを耐量子暗号といいます.
その中でも今回は格子暗号を紹介します.
本格的な内容は次の記事で....