格子暗号
格子暗号とは,格子点探索問題と呼ばれる数学的問題を高速に解くのが難しいという仮定を根拠に安全性を保証する暗号方式です.
格子暗号の実現には主に$4$つの方式があり,以下です.
・AD方式
・GGH方式
・NTRU方式
・LWE方式
ちなみに筆者はNTRU方式を頑張って勉強しています(聞いてない)
この記事の暗号化のセクションでは,格子暗号の直感的イメージに近いGGH方式に沿って解説をしようと思います.
それではまず前提知識からです.
これらは知っている必要はなくて,そんなもんだと思って見てください.
証明も今回はしません(というかできない)
諸性質
まずは格子についてです.
ここでは簡単のため,$2$次元の場合のみを考えます.
一般的には$n$次元であることに注意してください.
格子とは格子点の集合です.
格子点とは,ある$2$つのベクトルの整数係数の線形結合として表される点をさします.
つまり格子とは,あるベクトル${\boldsymbol x_1}, {\boldsymbol x_2}$によって
$ \{ a_1 {\boldsymbol x_1} + a_2 {\boldsymbol x_2} \ | \ a_1, a_2 ∈ \mathbb{Z}\} $
と表されます.
ここで重要な性質を$1$つ挙げます.
性質$1$
ある格子を構成する基底は複数ある
この性質$1$のイメージは下の図$1$です.
図のうち,左のような基底$A$を直交型基底,右のような基底$B$を非直交型基底とよびます.
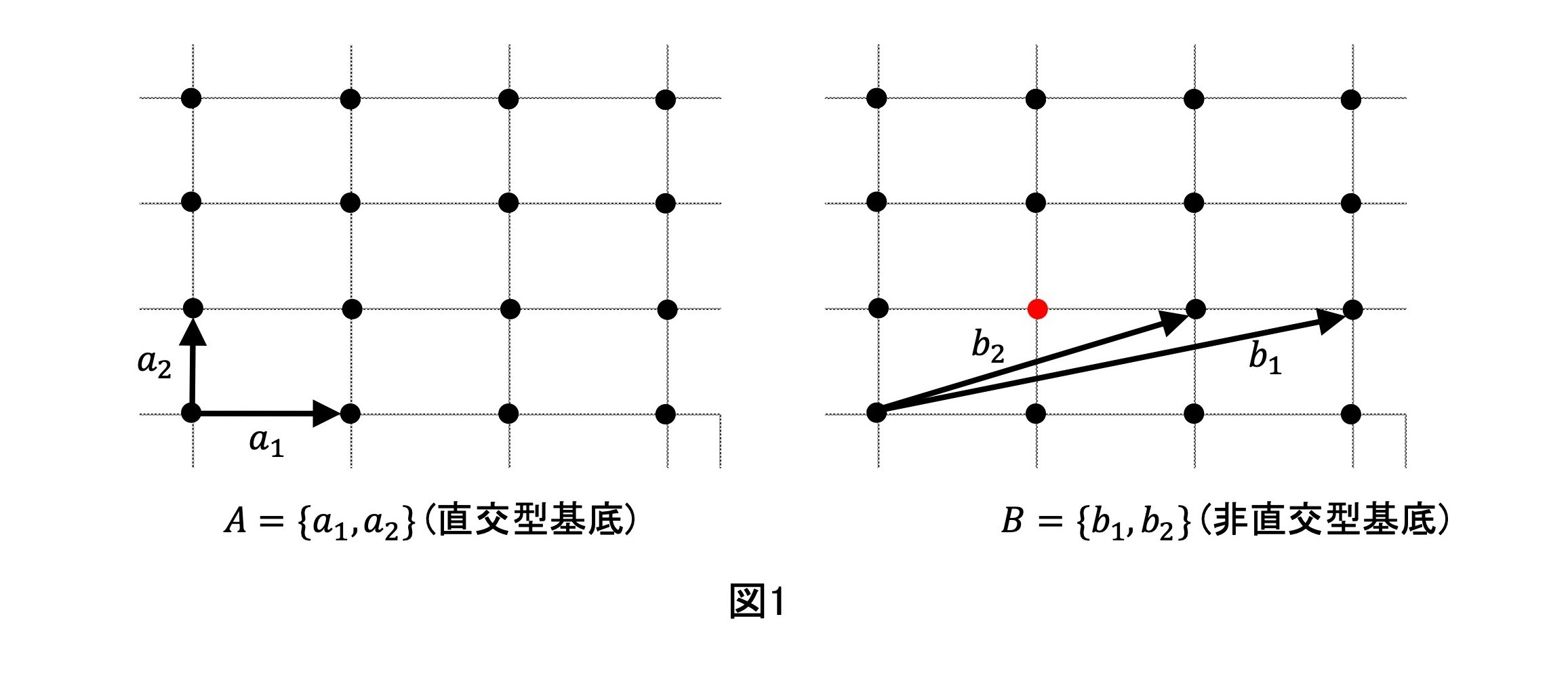
直感的にはわかりにくいですが,基底$B$で図$1$の任意の格子点を表現できます.
なぜなら,(この場合は)簡単な計算により
$-{\boldsymbol b_1} + {\boldsymbol b_2} = {\boldsymbol a_1}$
$3{\boldsymbol b_1} -2 {\boldsymbol b_2} = {\boldsymbol a_2}$
と基底$A$を基底$B$で表せるためです.
(ただし,一般的には基底$B$から基底$A$を計算するのは難しいです)
また,直交型と非直交型の基底の性質として以下のようなものがあります.
性質$2$ (直交型基底)
直交型基底からは任意の格子点を計算しやすい
性質$3$ (非直交型基底)
非直交型基底からは任意の格子点を計算しにくい
直交型基底では,上の図$1$のように単純に基底を組み合わせれば任意の格子点を計算できる様子が直感的にわかると思います.
一方で,非直交型基底では基底を複雑に組み合わせなければ任意の格子点を表現することは難しいです.
例えば上の図$1$において,赤色の格子点は
$-{\boldsymbol b_1}+2{\boldsymbol b_2}$
と表されます.
この程度であれば少し考えれば楽に計算できますが,少なくとも直交型よりは面倒であることがわかりますね.
これらの基底${\boldsymbol b_1}$と${\boldsymbol b_2}$は,長さが大きく平行に近いほど計算が難しくなることが知られています.
また,直交型と非直交型とでは以下のような相互関係があります.
性質$4$
直交型基底から非直交型基底は容易に計算できる
非直交型基底から直交型基底を計算するのは難しい
上の図$1$の例では簡単なものを挙げたので基底$B$から基底$A$を計算できましたが,一般的には難しいということが知られています.
公開鍵暗号の安全性は,公開鍵から秘密鍵を計算するのが難しいという前提により成り立っています.
つまりこの性質$4$が安全性に直結するということです.
前提となる性質はこのあたりで,いよいよ暗号化と復号の話です.
暗号化と復号
AliceからBobに平文$m$を送ることを考えます.
公開鍵暗号なのでまずはBobが公開鍵と秘密鍵を作ることから始めますが,その前にBobは格子の空間の次元$n$を決めて公開しておきます.
ここでは簡単のため上の例に合わせて$n=2$のときの平面を考えることにします.
鍵生成
Bobの秘密鍵は直交型基底$A=\{ {\boldsymbol a_1}, {\boldsymbol a_2}\}$で,公開鍵は非直交型基底$B=\{ {\boldsymbol b_1}, {\boldsymbol b_2}\}$です.
ここで,${\boldsymbol a_1}, {\boldsymbol a_2}, {\boldsymbol b_1}, {\boldsymbol b_2}$はそれぞれ$2$次元ベクトルとします.
暗号化
まずAliceは平文$m$を$2$つの整数$m_1, m_2$として表しておきます.
そしてこの平文$m_1, m_2$とBobの公開鍵$B$によって
${\boldsymbol g} := m_1{\boldsymbol b_1} + \times m_2 {\boldsymbol b_2}$
を計算します.
この点を$G$とでもおくと,$G$はBobが生成した格子点の$1$つになっています.
下の図$2$では,格子点$G$を表すベクトルは
${\boldsymbol g}=7{\boldsymbol b_1}-3{\boldsymbol b_2} \ \ \ \ \ \ (m_1=7, m_2=-3$ということ$)$
と表されます.
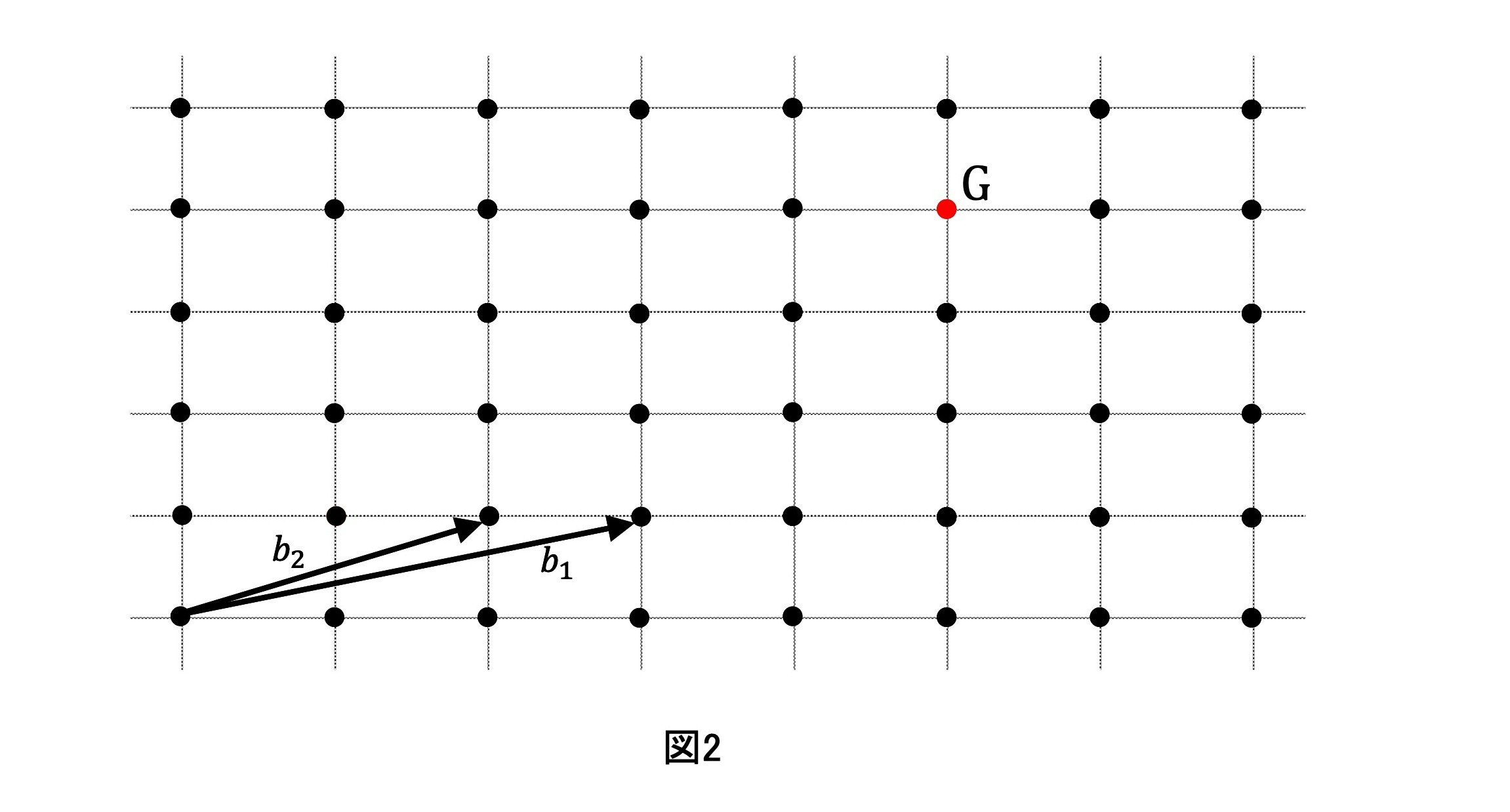
次に,Aliceは$2$つの小さな実数として$r_x, r_y$をランダムにとってきます.
そしてこれらの値を格子点$G$に加えてあげたものが暗号文${\boldsymbol c}$です.
(暗号文${\boldsymbol c}$に対応する点を$C$とおいておきます)
つまり,${\boldsymbol r} = (r_x, r_y)$とおくなら,
${\boldsymbol c} := {\boldsymbol g} + {\boldsymbol r}
$
$=(m_1{\boldsymbol b_1} + \times m_2 {\boldsymbol b_2}) + {\boldsymbol r}$
です.
ただし制約として,点$C$に最も近い位置に先ほどの格子点$G$が来るように$(r_x, r_y)$を選ぶとします.
(要は$r_x, r_y$は小さい実数ということです)
例えば下の図$3$のようになります.
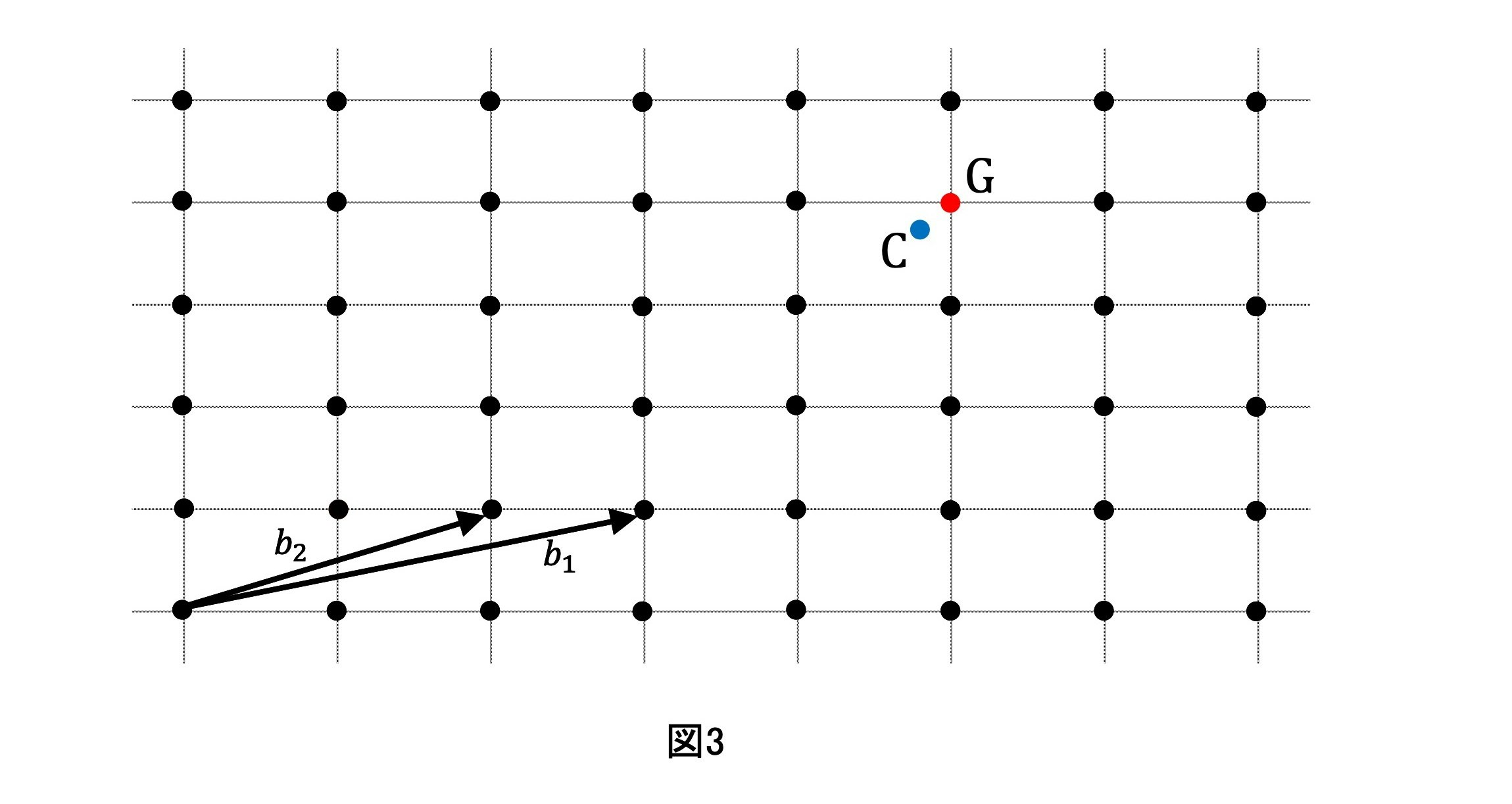
ここで,意味を考えてみます.
性質$2$より,秘密鍵$A$は任意の格子点を計算しやすいので,Bobは点$C$に最も近い格子点$G$を計算できそうですね.
性質$4$より,公開鍵$B$から秘密鍵$A$を計算するのは難しいです.
また性質$3$より,公開鍵$B$は非直交型基底なので,点$C$に近い格子点$G$を$B$から計算するのは難しいです.
これらをまとめると,秘密鍵$A$は第三者は簡単に求められそうになく,秘密鍵$A$を持っているBobだけが復号を容易に行えます.
復号
Bobは秘密鍵$A$と暗号文${\boldsymbol c}$から,格子点$G$を計算します.
$A$は直交型基底だったので,格子点全体を容易に計算でき,格子点$C$に最も近い格子点$G$も容易に計算できます.
さらに格子点$G$と公開鍵$B$から連立方程式を立て,解くことで平文$(m_1, m_2)$が得られます.
具体的には
${\boldsymbol g} = m_1{\boldsymbol b_1} + \times m_2 {\boldsymbol b_2}$
という式から得られる$2$本の方程式を連立すればよいです.
この連立方程式はガウスの消去法とよばれる方法などで高速に解けます.
最後に
本当はもっと議論する内容はあるのですが,記事が特大ボリュームになってしまうのでこのあたりにしておきます.
細かい話を省略したり,敢えて曖昧な議論をしているところもあるので興味がある人は自分が参考にしたページを見てみてください.
下の方に貼っておきます.
参考
清藤武暢/青野良範/四方順司(2015)『量子コンピュータの解読に耐えうる「格子暗号」の最新動向』
https://www.imes.boj.or.jp/research/papers/japanese/kk34-4-7.pdf
青野良範(2013)孔子暗号の実用化に向けて
https://www.nict.go.jp/publication/NICT-News/1303/02.html