こういうことらしいので勉強がてら累積和の基本的なところをまとめてみます
累積和とは
一定区間の和を少ないオーダーで取得できるように準備しておいて,ほしい値を高速に取り出そう!
というものらしい(雑
つらい足し算
詳しいことはわかりませんが見てみましょう。
次のようなリストAがあるとします。
このリストの一定区間の和を何度も何度も問われそうだと脳内に直接話しかけられた時,毎回その区間の和を愚直に求めていては無駄な計算が多いです。
例えば0番目から7番目までの和,つまりこのリスト全体の和を100回問われる時,
A[0]+A[1]+...+A[6]+A[7]
と100回計算していては遅いということです。
そこで累積和が大活躍するわけです。
ついに登場累積和
効率よく値を取得するために,リストAからもう一つリストを生みだします。
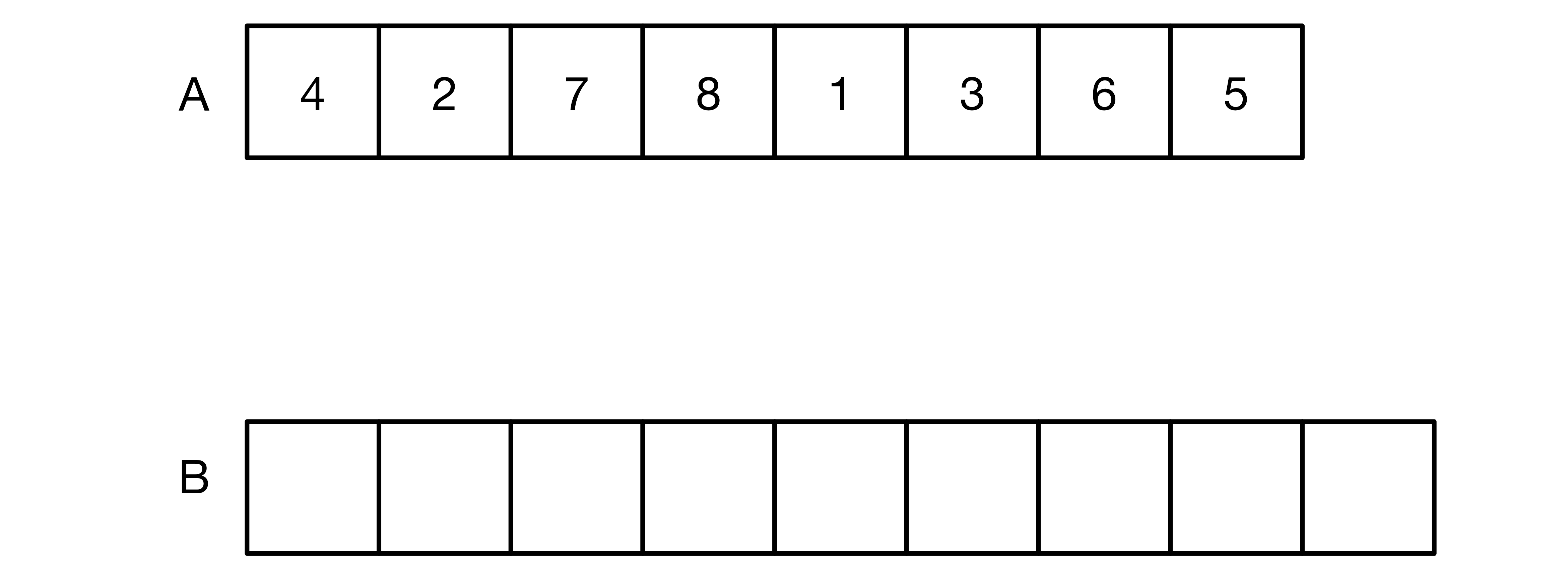
この生み出されれたリストB,これをどう更新するかが肝になります。
このリストに格納するものはもちろんリストAと関わりのある値で,
B[n]にはA[n-1]までの和
が格納されます。
少しややこしいですが,次の図を見るととても良く分かる!!(気がする
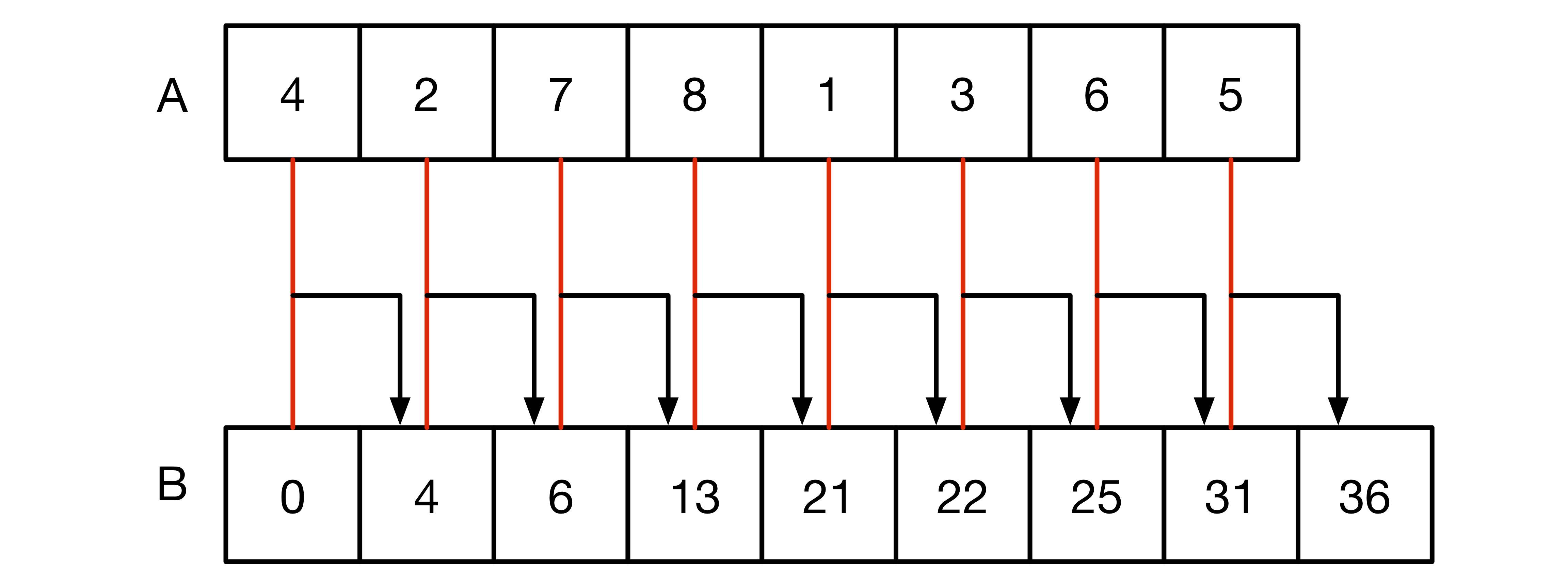
左端から見てみましょう。
- B[0]:A[-1]までの和 → 存在しないので0
- B[1]:A[0]までの和 → A[0]とその前までの和であるB[0]の和
- B[2]:A[1]までの和 → A[1]とその前までの和であるB[1]の和
- ……
- B[8]:A[7]までの和 → A[7]とその前までの和であるB[7]の和
こうしてみていくと図の赤い線で結ばれているものの和が矢印先に格納されることになります。
これで先程の全体の和を100回聞かれたときに何度も全体を足さなければならない問題は解決ですね,B[8]を100回出力してあげれば良いのです。
そして最初の方で述べたように,全体の和だけでなくある区間の和を高速に取り出すことも可能になっています。
数学強者の方々はもう理解できていたりするのでしょうか。僕は未だに直感的理解です()
ある区間の和
用意したリストBを使って指定されてた区間の和を求めてみましょう。
ここでは例としてA[2]〜A[4]の和を取り出してみます。
愚直に考えればA[2]+A[3]+A[4]ですが,もちろんそうはしません。
左から次々と足して作ったリストBの特性を使って値を求めるとこうなります。
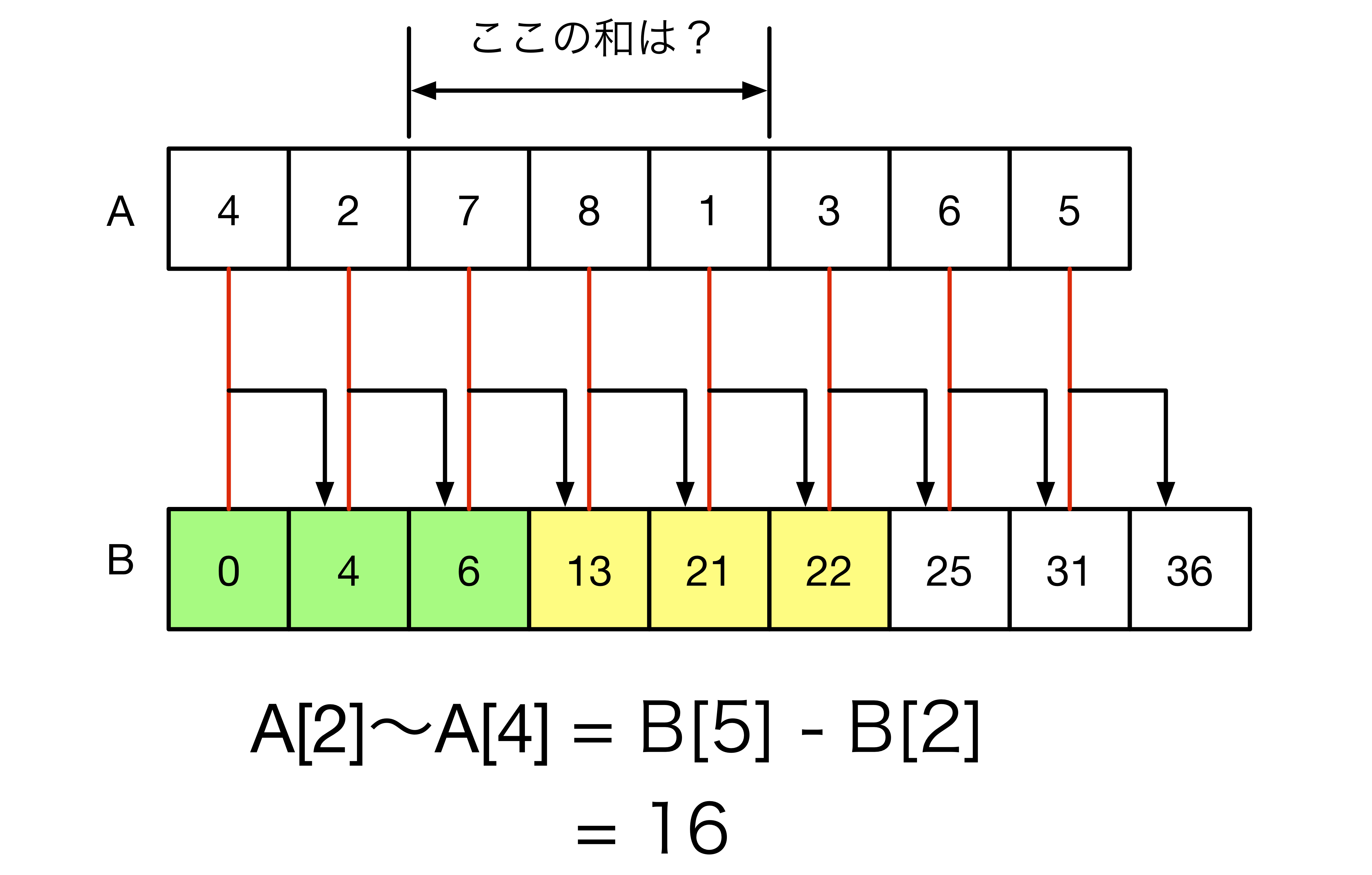
謎の引き算により一発で出ました。
色に注目すると少しわかりやすいかも知れません。A[2]〜A[4]の和が今回欲しい情報で,つまりA[4]までの和が格納されているB[5]から後ろ,黄色の区間までで行われた計算になります。
この時B[5]だと図の緑色になっている区間で計算した値は不必要なものとなるので,引いてしまえば良いです。
簡単ですね!(理解できてないけど)
一般化すると次のように求められますね。
区間a~bの和:B[b+1]-B[a]
問題を解いてみる
実際にAtCoderに出題された問題で累積和を使うと解くことができる問題を解いてみましょう。
今回はこれを解きます
AtCoder Beginner Contest 130: D - Enough Array
コード全体としてはこちらから見られます。キレイでは無いですが温かい目で眺めていただけると幸いです。
累積和リストつくろう
入力を雑にこんな感じで取って……
int n;
long long k;
cin >> n >> k;
長さNの整数数列Aはもう入力取りつつ累積和リスト作っちゃって良さそうですね。
ただ先頭に0が入るので要素数はN+1とします。
(あとリストリスト言いつつvector使っちゃいます)
vector<long long> A(n+1);
A[0] = 0;
for (int i=1; i<=n; i++) {
int a;
cin >> a;
A[i] = A[i-1] + a;
}
問題を解こう
ここまでこればあとは入力Kを超える和を持つ範囲を数えれば優勝ですね!
最後に出力してしっかりAC(Accepted)観測しました
long long ans = 0;
int left = 0;
int right = 0;
while (right < n) {
if (A[right+1]-A[left] >= k) {
ans += n - right;
left++;
}
else {
right++;
}
}
cout << ans << endl;
基本的には上で説明した方法で累積和のリストを活用しているだけなので,範囲を表す変数left,rightを用意してあげて,A[right+1]-A[left]がKを超えるかどうかチェックしています。
でもなんか変なことしてますね,単純に全探索はしてません。
これAは1以上の整数なのである範囲がKを超えることが分かった時点で右に残っているやつらを足してもK超えるということが確定します(説明力ほしい
例えばA[0]~A[9]があったとして,A[0]~A[5]の和がKを超えると分かった場合,次の範囲も確実にKを超えます。
A[0]~A[6]A[0]~A[7]A[0]~A[8]A[0]~A[9]
つまりA[0]を始点とした時にA[5]までの和でKを超えると分かった時,数列の長さNからrightである5を引いてあげれば残りの和を確かめるまでもなく,その数が分かるよねというお話でした。
あとはいい感じにleftとrightをインクリメントしてあげて,右端についたら出力,優勝です。
まとめ
使い所に気づくことができればそんなに難しいことなく解けたりするのでは?とか思ったり思わなかったり。
仕組み自体は複雑では無いと思うので,一定区間の和だったりを何度も求めなければならないような気がしたときは,試しに実装してみると良いかも知れません。