つい最近まで、囲碁でのAIとプロ棋士の勝負はまだ10年かかると言われていました。しかし、今年3月にGoogle DeepMindの人工知能(AI)「AlphaGo」は李世乭九段に4勝1敗という歴史的大勝を実現しました。
どうしてもその強さの秘密を知りたい!「TensorFlowチュートリアル - 熟練者のためのディープMNIST」を実行できるレベルのAI初心者なのに、頑張ってAlphaGoを理解しようとする試みに挑戦しました。この記事はそのメモです。
主な参考文献は、下記のとおりです。
- Mastering the Game of Go with Deep Neural Networks and
Tree Search - 囲碁AI “AlphaGo” はなぜ強いのか?
- RocAlphaGo Project Wiki
AlphaGo基本構成
一言で言えば、MCTS+ConvNetです。
- MCTS:モンテカルロ木探索(Mote Calo Tree Search)。モンテカルロ=ランダム
- ConvNet:畳み込みニューラルネットワーク
MCTSもConvNetもが10年以上前の技術であり、DeepMindの発明ではありません。
MCTS
MCTSについては、ちょっと古いがモンテカルロ木探索法が分かりやすいです。要するに、最後までランダムにやってみることです。これはプレイアウトと呼ばれます。
「The Power of Forgetting: Improving the
Last-Good-Reply Policy in Monte Carlo Go」によると、プレイアウトは下記の3段階に分けることができます。
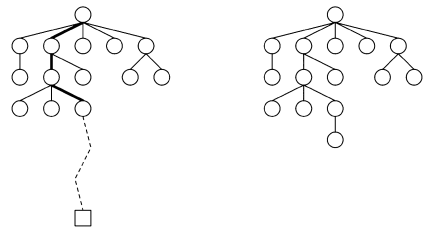
- 選択:既存の探索木からパスを選択します。下記の図の太線の部分。
- サンプリング:決着までランダムに手を打ってシミュレーションします。下記の図の点線の部分。
- 逆伝播:各ノードの勝率を更新し、新しいノードを追加します。
すべてのノードに対して、決着がつくまでシミュレーションすることが時間的に不可能です。有望な手を予測する「ポリシー」が必要となってきます。これは、AlphaGo以前のアプリも普通にやっていることです。しかし、線形モデルで予測するので、せいぜいアマチェアレベルです。AlphaGoは、線形モデルをConvNetに置き換えてプロレベルに進化しました。
ConvNet
AlphaGoでは、下記の3つのネットワークを利用しています。
- ポリシー・ネットワーク:「この局面において専門家ならどんな手を打つか」を答えるConvNetです。専門家の経験です。
- バーリュ・ネットワーク:「この局面においてどっちが勝つか」を予測するConvNetです。専門家の感です。
- ファスト・ネットワーク:ポリシー・ネットワークは精度が高いが遅いので、プレイアウトで高速評価のためにファスト・ネットワークを利用します。
学習方法
ポリシー・ネットワークの教師あり学習
「TensorFlowチュートリアル - 熟練者のためのディープMNIST」と同じやり方です。下記のような画像データをConvNetに入力し、識別結果を正解のラベルと比較します。

熟練した人間のプレイヤの対戦データから、(局面、次の手)のペアを抽出できます。下記のような局面をポリシー・ネットワークに入力し、一番確率の高い出力結果を実際の次の手と比較します。
KGS Go Serverから取得した3千万データで学習させた結果、57%の精度で熟練した人間のプレイヤの次の手を予測できるようになりました。
ファスト・ネットワークの教師あり学習
Tygemサーバの8百万データで線形モデルのファスト・ネットワークを学習させた結果、24.2%の精度となりました。しかし、速度はポリシー・ネットワークの1,500倍です。
ポリシー・ネットワークの強化学習
強化学習は、教師あり学習のように入力と出力のペアが与えられることがありません。エージェントが行動を選択することで環境から報酬を得ます。ここでの報酬は、対戦の結果となります。勝った場合は、そこまでの手をより高い確率で選択するようにパラメータを調整します。
対戦相手は、自分自身です。厳密に言えば、ランダムに選んだ自分自身の古いバージョンです。単一のポリシーの過学習を防ぐために。
数百万回の強化学習の結果、教師ありポリシー・ネットワークとの対戦で80%以上の勝率となりました。さらに、一番強いオープンソースのGoアプリのPachiとの対戦で85%以上の勝率となりました。Pachiは10万回のシミュレーションで次の一手を決めます。それに対して、AlphaGoは全然探索していません。強い!
バーリュ・ネットワークの強化学習
ポリシー・ネットワークが強くなったら、次はバーリュ・ネットワークの学習です。ポリシー・ネットワークは完璧なプレーに近いプレーができると考え、ある局面から対戦結果を予測するように、バーリュ・ネットワークを学習させます。
ここは難しいところ。囲碁は、将棋やチェスなどのゲームに比べると、数値化することが難しいからです。
技術的にも難しい問題が発生しました。KGSデータで学習させた結果、過学習となりました。同じゲームの入力データは独立ではないからです。
解決方法はとてもスマートです。ポリシー・ネットワークの強化学習で集めた対戦データを使って、1ゲームから1局面だけ抽出し、過学習問題が解決されました。
この時点で、バーリュ・ネットワークは、ファスト・ネットワークによるプレイアウトより、予測精度が高いです。15,000倍も早い速度で、ポリシー・ネットワークによるプレイアウトと近い精度が実現されました。
再び、ポリシー・ネットワークの強化学習
もう一回、ポリシー・ネットワークの強化学習です。しかし、今回は、自己対戦の結果ではなく、バーリュ・ネットワークの予測との違いで、パラメータが調整されます。ポリシー・ネットワークとバーリュ・ネットワークの整合性を高めるための学習です。
システム結合
それぞれのシステムができたので、次はポリシーとバーリュ・ネットワークを使ってモンテカルロ木探索を行う時期です。
探索木のすべてのルートに、下記の3つの値がついています。
- 評価値:評価値の高いルートを優先的に選択します。
- 訪問回数:訪問回数の低いルートを優先的に選択します。
- 事前確率:事前確率の高いルートを優先的に選択します。
評価値は、下記の2つの方法で計算されます。最終結果は、中間結果の重み付け合計で求めます。
- バーリュ・ネットワークで計算します。
- ファスト・ネットワークによるプレイアウトで計算します。
訪問回数は、あるルートを利用した回数です。新しいルートの探索を奨励するために、訪問回数の低いルートを優先的に選択するようになりました。
事前確率は、初めてあるノードを評価する際に、1回だけ教師あり学習のポリシー・ネットワークで計算されます。熟練した人間のプレイヤは幅広い良い手を選択するので、強化学習のポリシー・ネットワークより、教師あり学習のポリシー・ネットワークのほうがパフォーマンスがよいです。しかし、バーリュ・ネットワークの強化学習では、強化学習のポリシー・ネットワークのほうがパフォーマンスがよいです。
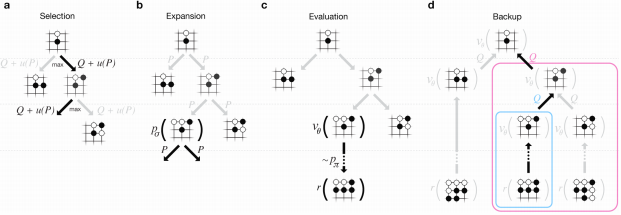
- aの選択段階では、値の高いルートを選択します。
- bの拡張段階では、新しいノードの事前確率を計算します。
- cの評価段階では、バーリュ・ネットワークとプレイアウトで勝負を予測します。
- dのバックアップ段階では、親ルートの値を更新します。
コスト
ポリシーとバーリュ・ネットワークは精度が高いが、計算量も多いです。MCTSとConvNetを結合するために、シミュレーションをCPUで、ポリシーとバーリュ・ネットワークをGPUで実行させる必要があります。
最終版のAlphaGoは、48CPUと8GPUで稼働します。李世乭九段との試合で使われたのは、AlphaGoの分散版であり、1202CPUと176GPUで稼働します。
コストについては、AlphaGoの運用料金は30億円以上?や、AlphaGoのサーバ料金は最低60億円!!?との説もあります。
コストパホーマンスの意味では、人間はまだ負けていません。