Quantum Error Correction Todd A. Brun 1
初めまして!量子エラー訂正超初学者です。読んだ論文を細切れにして投稿します。
だいぶ読みにくくなってしまいました。。。時間のある時に編集します。
##シュレディンガー方程式について
φは状態ベクトルである。ハミルトニアンHを持ち、これは系がどのように発展するかにおいて完全な情報を与えてくれる。
その結果として、ユニタリ発展を持ち、例えば状態|0>をU|0>にする。
##CPTPマップ
一般的に、量子状態は混合状態も含めて、密度行列の形で表される。
密度行列の性質
①トレースが1
②正値
純粋状態はp=|φ><φ|で表されるが、これはランク1の射影行列である。
時間発展してもこの性質は保存されるが、密度演算子の時間発展には、更に
・線形性
・トレース保存
・完全正値
これらを満たしたとき、CPTPマップという。下のような式で状態の時間発展がかかれる。
Akはクラウスオペレータと呼ばれる。
確率
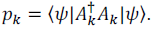
でランダムに選ばれたAによって次の状態が決まる。
どの状態が選ばれるかわからないので、∑を取ってすべての演算子を混合(足す)して考える。
同様に、この時間発展をユニタリーオペレータで記述するとしたら、
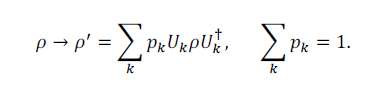
である。ここで、P=∑pk|φk><φk|であり、Pは密度行列(量子状態を混合状態混みで表現したもの)を、確率pkである状態|φk><φk|になったとすると、その総和が、Pである。

