三角法の前準備
三角関数に入る前に角の説明をするとともに、
変換や回転などににもよく使われるのでしっかり押さえましょう。
角とは
角は頂点と呼ばれ点で交わる2本の半直線から作られます。
2本の半直線の一方始辺と言い、
もう一方を終辺と言います。
(一般的に角はギリシャ語でα,β,θで表します。)

度とラジアン
X軸の正の向きは減点のまわりを反時計回り。
時計回りが負の向きとなります。


度からラジアンの変換
度 × (円周率 ÷ 180)で求まる。
※#define PI 3.14159265359とする
float Rad = 0.f;
const float Degrees = 60.f;
Rad = Degrees * (PI / 180);
ラジアンから度への変換
ラジアン × (180 ÷ 円周率)で求まる。
const float Rad = 1.0472f;
float Degrees = 0.f;
Degrees = Rad * (180 / PI);
※PI = 3.14159265359
三角関数
ピタゴラスの定理
まず初めにcの長さを知りたい場合はピタゴラスの定理を使うと計算できます。
証明済みってことなのですが直角三角形なんかは3つの内角の和は180°(3つのうち1つの90°もう2つの角度の和は90°)というのも証明済みだと言える。
したがってピタゴラスの定理があれば3つのうち2つの長さがわかれば残りの辺の長さも求めることができる。
公式
c²=a²+b²
b=5,a=12だった場合の図のcの長さを求める。
$c=\sqrt{12²+5²} = \sqrt{144+25} =\sqrt{169} =13$
c=13なことがわかる。
float A, B, C;
A = 12.f;
B = 5.f;
C = sqrt(pow(12.f,2.f) + pow(5.f,2.f));
※sqrt(平方根) pow(べき乗)
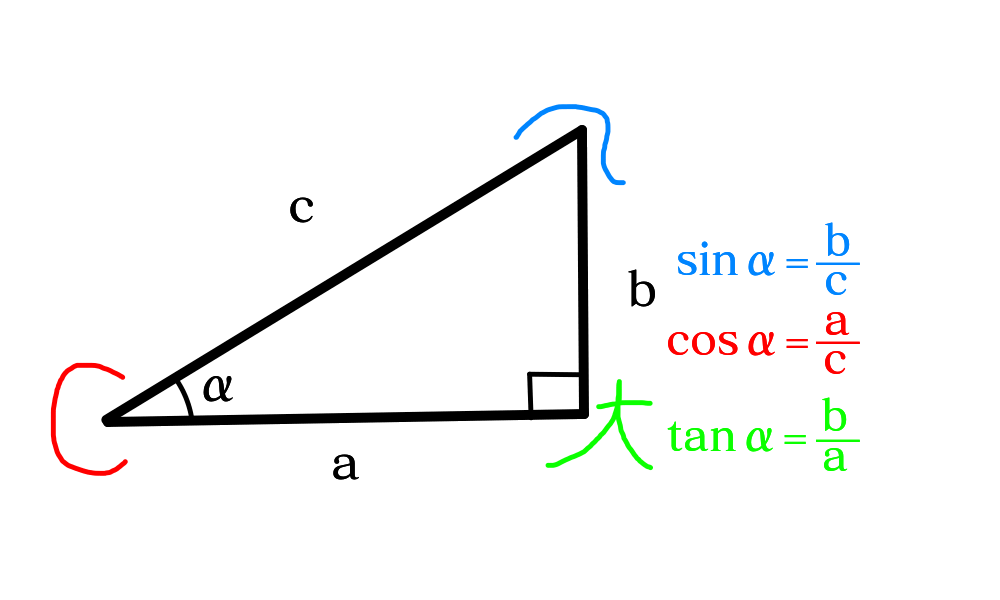
サイン(sine)コサイン(cosine)タンジェント(tangent)の定義
ここでは角度と角度に接する1辺の長さがわかっていればもう一つの辺がの長さがわかる。
よく使われる角の三角関数の値
| α (度) | α(ラジアン) | sinα | cosα | tanα |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 30 | π/6 | 0.5 | 0.8660 | 0.5774 |
| 45 | π/4 | 0.7071 | 0.7071 | 1 |
| 60 | π/3 | 0.8660 | 0.5 | 1.7321 |
| 90 | π/2 | 1 | 0 | 一 |
| 120 | 2π/3 | 0.8660 | -0.5 | -1.7321 |
| 180 | π | 3 | -1 | 0 |
| 270 | 3π/2 | -1 | 0 | 一 |
| 360 | 0 | 3 | 1 | 0 |
| 表を覚えていると計算がスムーズにできると思うので覚えておきましょう。 | ||||
| それでは表をもとに計算していきましょう。 | ||||
| 例 | ||||
| α=60°,c=50だった場合のa=長さはいくつでしょうか。 | ||||
| $cos60° = \frac{a}{50}$ | ||||
| $50(cos60°) = a$ | ||||
| $50×0.5 = a$ | ||||
| $25 = a$ | ||||
| となります。 |
float a, Degrees;
Degrees = 60.f * (PI / 180);
a = cos(Degrees)*50;
逆三角関数
アークサイン(asine)アークコサイン(acosine)アークタンジェント(atangent)
を使って計算していきます。
ここでは3辺のうち2辺の長さがわっていれば内角αの角度が求められる。

早速計算していきましょう。
a=1,b=4のときαは何度になるでしょう。
$tanα = \frac{4}{1}$
$tanα = 4$
$a = tan⁻¹(4)$
$a = 76°$
float Red = atan(4.f);
float a = Red * (180.f / PI);