ローカル座標とワールド座標
ここで一番重要なのがどころから見た座標系なのかを意識する必要がある。
ゲーム開発をしていく上でとても重要で、のちのち大きさミスに繋がる可能性があるので十分注意してください。
ローカル座標
オブジェクト固有に空間の座標系をローカル座標と言う。
ワールド座標
座標系を備え座標によって任意の座標を指定できる空間のことをワールド座標と言う。
変位
変位 = 最終位置 - 最初の位置 で変位をもとめることができる。
※後引く先で覚えておくと覚えやすいです。
例
最初の位置が200ピクセルで最終位置が450ピクセルの場合
500 - 200 = 300ということがわかる。
ベクトルについて
ベクトルではよく矢を使って表し、矢の長さがベクトルの大きさを示し、矢の向きがベクトルの向きを指します
。
ベクトルの加法(ベクトルの足し算)
ベクトルの足し算は始点と終点を使って行い、ベクトルは1かっしょに固定されません。
矢の長さと向きが同じであればどこに移動しても大丈夫なのです。
ベクトルAの終点がベクトルBの始点になるように移動する。
そうすることにより、A + B = Cが計算できる。

すなわち、ベクトルAに沿って走り、次に向きを変えベクトルBに沿って走ったことと同じことを指すのです。
ベクトルの加法の交換法則
いかなるベクトルAとBに対しても
A+B = B+Aが成り立つ。

ベクトルの減法(ベクトルの引き算)
ベクトルAの向きを逆にして、終点と最初のベクトルの始点にくるようにします。
そうするためにはベクトルBを逆にし、負にしたものを足すのと同じ要領でやってきます。
A - B = C

ベクトルのスカラー倍
ベクトルの正規化
正規化とはベクトルの大きさを1にすることを言います。
具体的に向きは必要だけど大きさに正確な値が必要ないときは正規化をすることにより計算をしやすくします。
内積(スカラー積)
 内積の公式
2次元ベクトル
$\vec{A} = [a_{1},a_{2}] \vec{B} = [b_{1},b_{2}]$
$ベクトル\vec{A}と{B}の内積 = \vec{A}・\vec{B} = a_{1}b_{1} + a_{2}b_{2}$
2次元ベクトル
$\vec{A} = [a_{1},a_{2},a_{3}]$ $\vec{B} = [b_{1},b_{2},b_{3}]$
$ベクトル\vec{A}と\vec{B}の内積 = \vec{A}・\vec{B} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$
例
$2次元ベクトルで\vec{a}=[1,2]・\vec{b}=[3,4]のとき内積\vec{A}・\vec{B}を求める。$
$\vec{A}・\vec{B} = 1×3 + 2×4$
$ = 11$
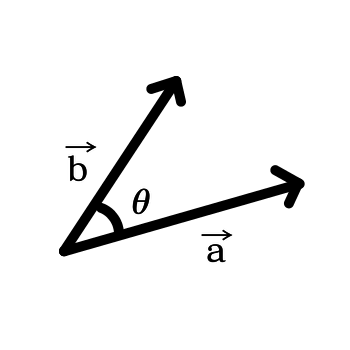
### なす角度
なす角度の公式
$ベクトル\vec{A}と\vec{B}のなす角度をθとすると$
$\vec{A}・\vec{B} = |\vec{A}||\vec{B}|cosθ$
※→はベクトルのこと。
例
$\vec{A} = [5,2,-1]\vec{B} = [8,1,-4]のとき、なす角度θは何度か。$
まず内積を求める。
$\vec{A}・\vec{B} = 5×8+2×1+-1×-4 = 40+2+12= 54$
次に必要なのが各ベクトルの大きさなので計算していきます。
$|A| = \sqrt{5^2+2^2+(-3)^2} = \sqrt{25+4+9} = \sqrt{38}$
$|B| = \sqrt{8^2+1^2+(-4)^2} = \sqrt{64+1+16} = \sqrt{81}$
これらを公式$\vec{A}・\vec{B} = |\vec{A}||\vec{B}|cosθ$に当てはめる。
$54 = \sqrt{38}×\sqrt{81}cosθ$
$\frac{54}{\sqrt{38}×\sqrt{81}} = cosθ$
$0.9733 = cosθ$
$θ = cos⁻¹(0.9733)$
$θ = 13.3°$
内積の公式
2次元ベクトル
$\vec{A} = [a_{1},a_{2}] \vec{B} = [b_{1},b_{2}]$
$ベクトル\vec{A}と{B}の内積 = \vec{A}・\vec{B} = a_{1}b_{1} + a_{2}b_{2}$
2次元ベクトル
$\vec{A} = [a_{1},a_{2},a_{3}]$ $\vec{B} = [b_{1},b_{2},b_{3}]$
$ベクトル\vec{A}と\vec{B}の内積 = \vec{A}・\vec{B} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$
例
$2次元ベクトルで\vec{a}=[1,2]・\vec{b}=[3,4]のとき内積\vec{A}・\vec{B}を求める。$
$\vec{A}・\vec{B} = 1×3 + 2×4$
$ = 11$
### なす角度
なす角度の公式
$ベクトル\vec{A}と\vec{B}のなす角度をθとすると$
$\vec{A}・\vec{B} = |\vec{A}||\vec{B}|cosθ$
※→はベクトルのこと。
例
$\vec{A} = [5,2,-1]\vec{B} = [8,1,-4]のとき、なす角度θは何度か。$
まず内積を求める。
$\vec{A}・\vec{B} = 5×8+2×1+-1×-4 = 40+2+12= 54$
次に必要なのが各ベクトルの大きさなので計算していきます。
$|A| = \sqrt{5^2+2^2+(-3)^2} = \sqrt{25+4+9} = \sqrt{38}$
$|B| = \sqrt{8^2+1^2+(-4)^2} = \sqrt{64+1+16} = \sqrt{81}$
これらを公式$\vec{A}・\vec{B} = |\vec{A}||\vec{B}|cosθ$に当てはめる。
$54 = \sqrt{38}×\sqrt{81}cosθ$
$\frac{54}{\sqrt{38}×\sqrt{81}} = cosθ$
$0.9733 = cosθ$
$θ = cos⁻¹(0.9733)$
$θ = 13.3°$
cos(コサイン)に関してわからない場合は下記に三角関数に関しての記事を書いておりますのでご覧ください。https://qiita.com/drafts/88e546dc10e465307bca/edit
外積(ベクトル積)
 外積の公式
$2つのベクトル\vec{A} = [a_{1},a_{2},a_{3}] \vec{B} = [b_{1},b_{2},b_{3}]とすると$
$\vec{A}と\vec{B}の外積は \vec{A}×\vec{B}=[(a_{2}×b_{3}-a_{3}×b_{2})(a_{3}×b_{1}-a_{1}×b_{3})(a_{1}×b_{2}-a_{2}×b_{1})]となります。$
例
$\vec{A}=[5,-6,0] \vec{B}=[1,2,3]のときの外積を求める$
$=[(-6×3 - 0×2)(0×1^5×3)(5×2 - (-6)×1)]$
$=[(-18-0)(0-15)(10+6)]$
$=[-18, -15 ,16]$
外積の公式
$2つのベクトル\vec{A} = [a_{1},a_{2},a_{3}] \vec{B} = [b_{1},b_{2},b_{3}]とすると$
$\vec{A}と\vec{B}の外積は \vec{A}×\vec{B}=[(a_{2}×b_{3}-a_{3}×b_{2})(a_{3}×b_{1}-a_{1}×b_{3})(a_{1}×b_{2}-a_{2}×b_{1})]となります。$
例
$\vec{A}=[5,-6,0] \vec{B}=[1,2,3]のときの外積を求める$
$=[(-6×3 - 0×2)(0×1^5×3)(5×2 - (-6)×1)]$
$=[(-18-0)(0-15)(10+6)]$
$=[-18, -15 ,16]$
※外積は交換不可能なので注意です。
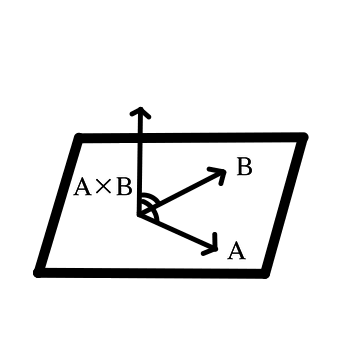
面法線
外積には、2つのベクトルのいずれも垂直な別のベクトルを作り出す性質があるため、外積を使って面法線を計算することができます。
面法線とはその面に垂直で長さが1の大きさを持つベクトルのことをいいます。
面法線公式
2つの3次元ベクトルをAおよびBとすると、
$面法線=(\vec{A}×\vec{B})= \frac{\vec{A}×\vec{B}}{|\vec{A}|×|\vec{B}|} $
例
$2つのベクトル\vec{A}=[5,-2,0]と\vec{B}=[1,2,3]の面法線を求める。$
$=[((-2)×3-0×2)(0×1-5×3)(5×2-(-2)×1)]$
$=[(-6-0)(0-15)(10+2)]$
$=[-6,-15,12]$
$\vec{A}×\vec{B}の大きさを求める$
$|\vec{A}|×|\vec{B}| =\sqrt{(-6^2)+(-15^2)+12^2} = \sqrt{36+225+144} = \sqrt{405} = 20.125$
$最後に\vec{A}×\vec{B}を正規化します。$
$[\frac{-6}{20.125},\frac{-15}{20.125},\frac{12}{20.125}] = [-0.298,-0.745,0.596]$
$\vec{A}×\vec{B} = [-0.298,-0.745,0.596]$
