PID制御とは
自動車の制御の一つにPID制御というものがあります.P,I,Dとはそれぞれ
P:Proportional(比例)
I:Integral(積分)
D:Differential(微分)
を意味しており,これらの3つの要素を組み合わせて制御対象を制御するものとなっています.
ここでは簡単に以下のような自動車の制御を考えることにします.
「一定速度で進む車と基準線があり,この車のハンドル角のみを制御することにより,車を点線に近づけます.」
車と点線との距離をCTE(Cross Track Error)と呼び,これを小さくします.
式にすると以下のような式になります.
steer = K_p \times cte + K_D \frac{d}{dt}cte + K_I \sum cte
ここで$K_P,K_I,K_D$をそれぞれ,Pゲイン(比例ゲイン),Iゲイン(積分ゲイン),Dゲイン(微分ゲイン)と呼ばれます.
P制御
P(比例)ゲインのみを用いて制御しようとすると下図のようになります.
基準線に近づき,線を通り過ぎ,再び基準線に近づき通り過ぎる,といったことを繰り返しています.この通り過ぎた部分のことをオーバーシュートと言います.
Pゲインのみで制御しようとすると,オーバシュートが発生し軌跡は振動的になってしまいます.またPゲインの値を大きくすると,素早くCTEを0に近づけようとしますが,振動が発散してしまいます.
このように,Pゲインのみを調整して制御することは困難であるということがわかります.
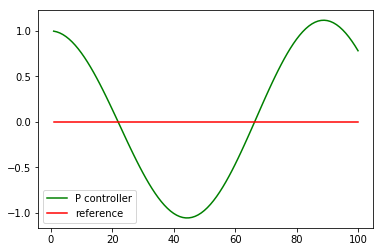
Fig.2 P制御
PD制御
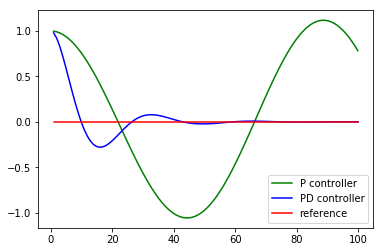
そこで,次にD(微分)成分を入れてみます.Dゲインを入れることで図のように,振動が収束していることがわかります.Dゲインは入力(ハンドル角)の変化量を抑える役割があります.
PD制御でも十分に目標値へ追従できていることがわかります.I(積分)ゲインが必要ないようにも思われます.それではI(積分)ゲインにはどのような効果があるのでしょうか?
ここで,次のような問題を考えます.
先ほどの自動車の例と同じものを考えますが,タイヤを取り付ける際に何らかのミスが生じ,少し傾いていることとします(現実では考えにくいですが...)
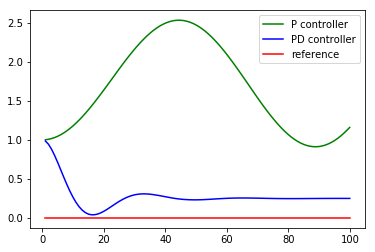
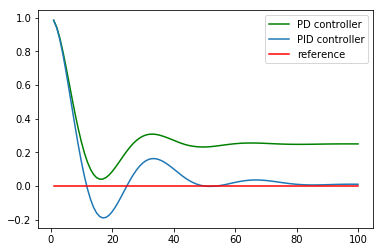
このとき,同じようにP制御とPD制御を適応すると以下の図のようになります.するとP制御は目標値から外れたところで振動し,PD制御は基準線に近づくものの,基準線との差が埋まらないまま,収束してしまっています.この差のことを定常偏差と言います.PD制御では定常偏差を解消することができません.
この定常偏差を減らすためにI(積分)ゲインが必要となります.
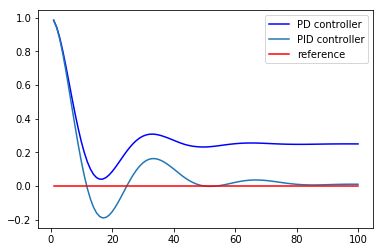
Fig.5 PID制御
PID制御
そこでI(積分)ゲインを入れてみます.
すると以下の図のように,定常偏差を解消することができました.
本記事では$K_p,K_I,K_D$の値については議論していませんが,実際にPID制御を適応する場合には,$K_p,K_I,K_D$のパラメータチューニングが必要となります.
本記事では厳密性は犠牲にしており,感覚的な議論となっています.ご了承ください.
次回の記事ではPID制御を用いることにより,シミュレータ上の自動車を制御します.PID制御の実装はC++を用います.
参考文献
はじめての制御工学 (KS理工学専門書)
制御工学の考え方―産業革命は「制御」からはじまった (ブルーバックス)
問題設定は以下を参照しました.
https://www.youtube.com/watch?v=-8w0prceask
PID制御のパラメータチューニングについてはこの動画がわかりやすいと思います.
https://www.youtube.com/watch?v=4Y7zG48uHRo&t=163s