この記事は筑波NSミライラボ Advent Calendar 2023 5 日目の記事です。
この記事では CSS だけでモンテカルロ法を用いた円周率の近似を実装したのでそれについて書きます。
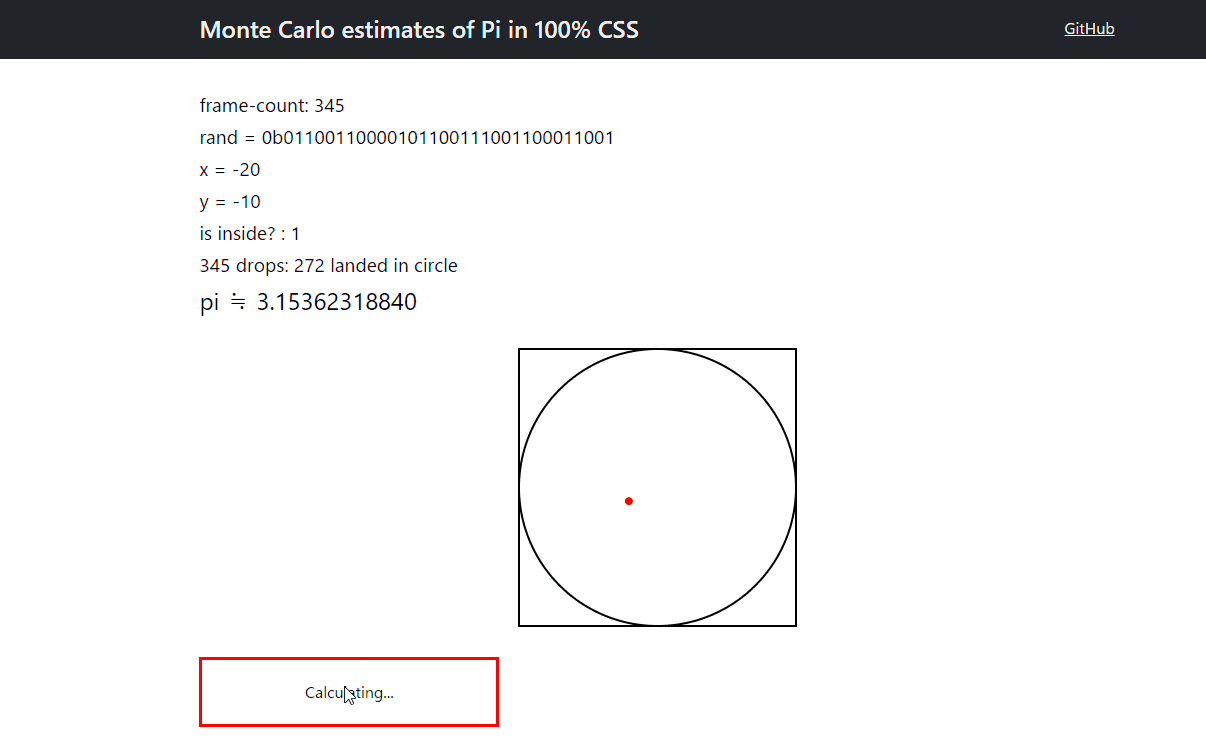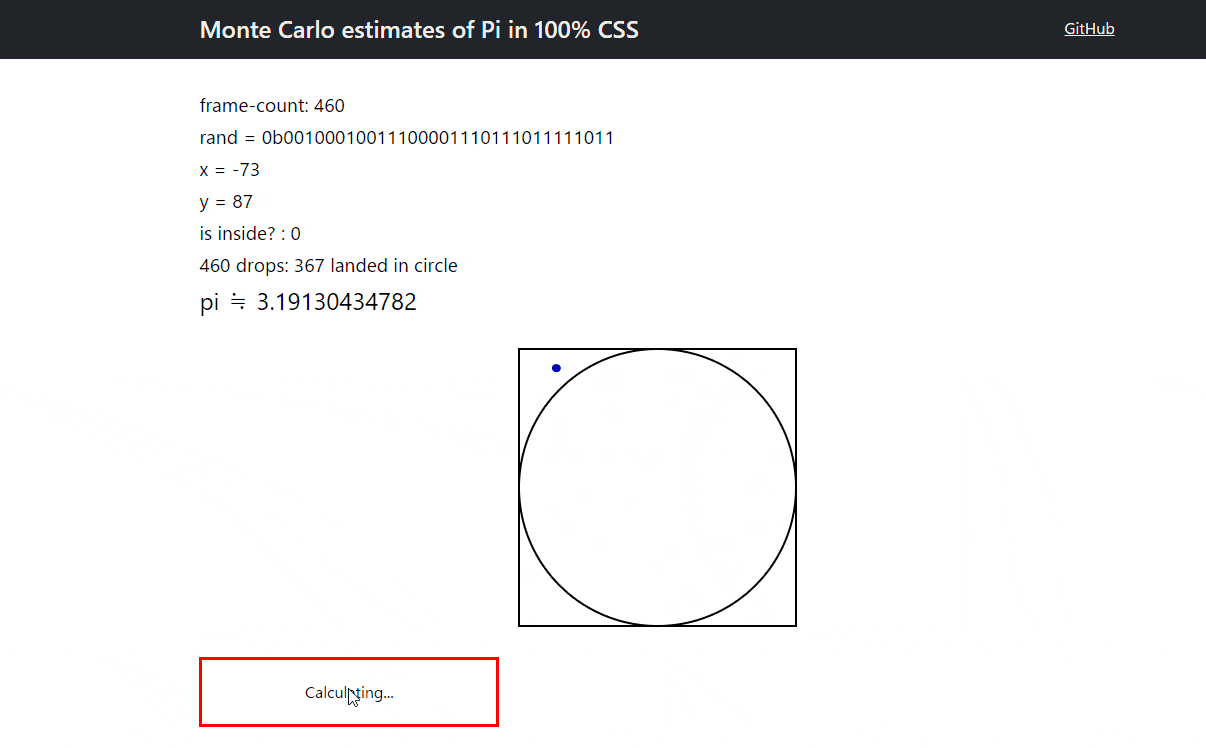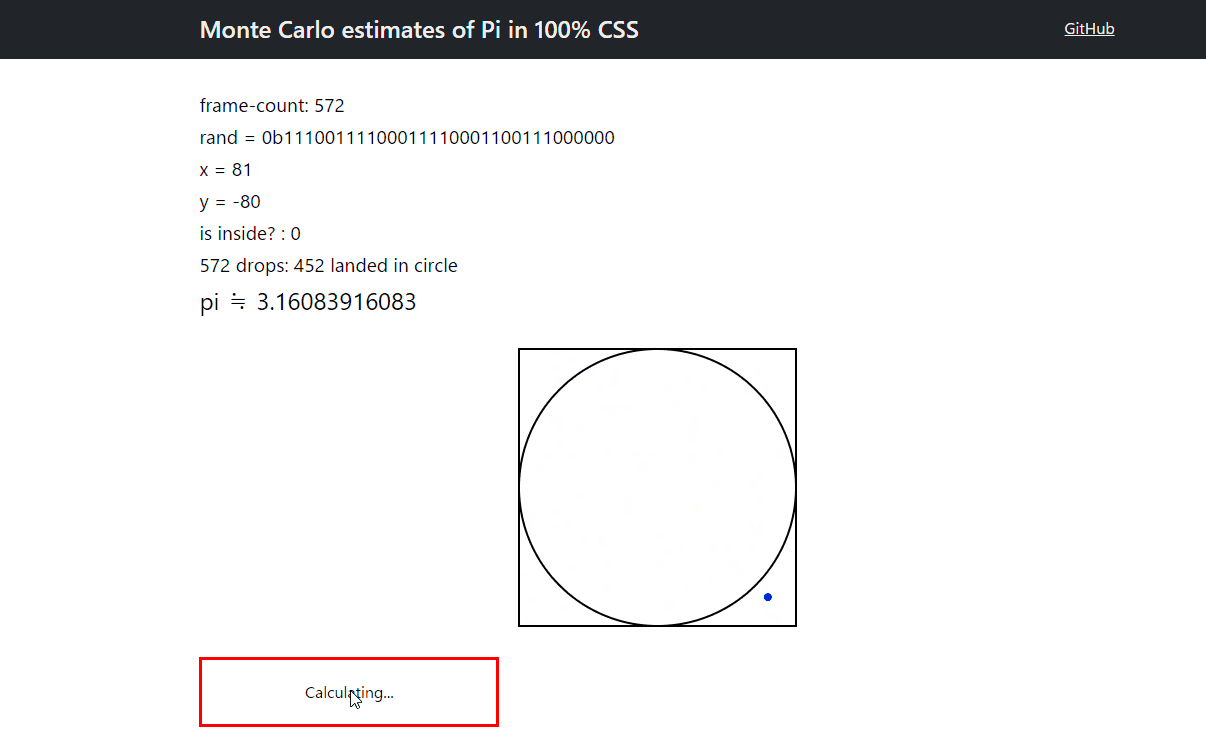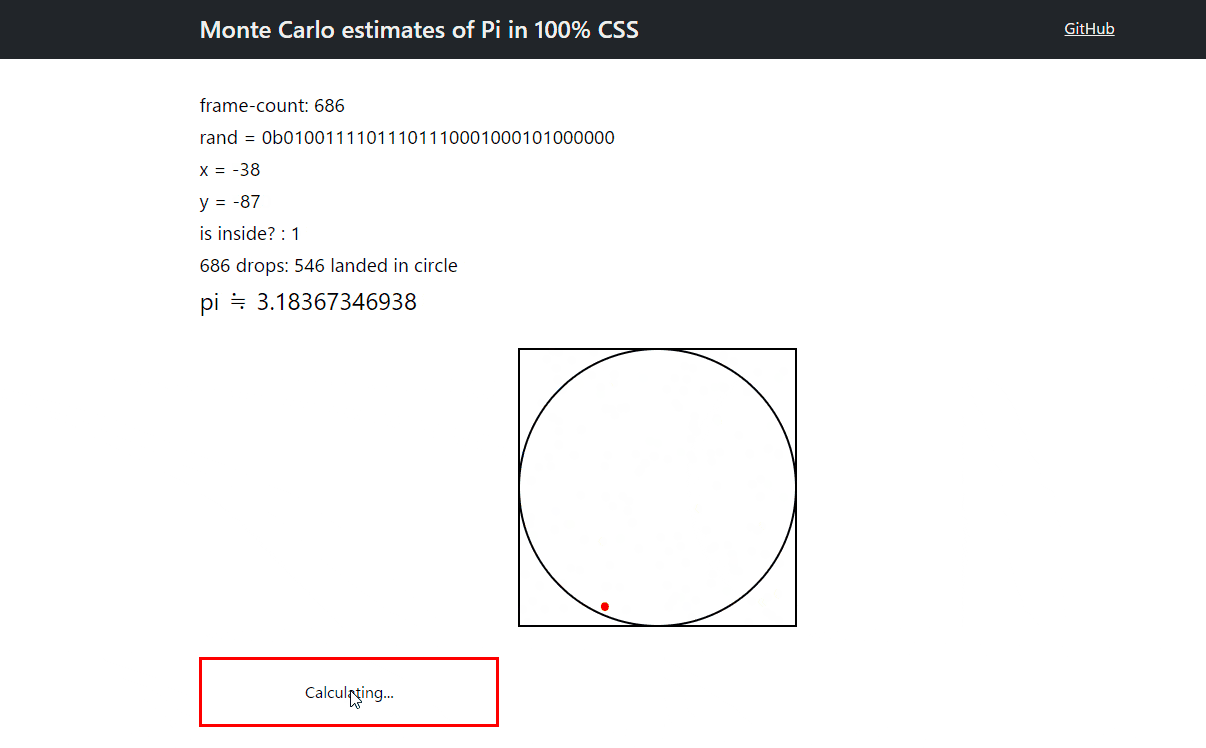
作ったもの
CSS だけです。JavaScript などは一切使っていません。
Chrome や Edge でのみ動作を確認しています。
リポジトリ (Star🌟お待ちしています!)
今回はこれを作る際に書いた CSS (monte-carlo-pi.css) で使ったテクニックなどについて書こうと思います。
モンテカルロ法とは
乱数を用いて何らかの値を見積もる方法をモンテカルロ法と言います。
モンテカルロ法の有名な例として円周率を求めるものがあります。
モンテカルロ法で円周率を求める
円周の長さを測らずとも円周率を求める方法があります。
一辺の長さが $l$ の正方形とそこに内接する円を考えます。
そしてこの正方形の中にランダムに一定数の点を打ち、円に入った点を数えることにより円周率を求めます。
正方形の面積は $l^2$ であり、円の面積は $(\frac{l}{2})^2\pi$ すなわち $\frac{l^2}{4} \pi$ です。
多くの点を打つと、ある領域に入った点の数は、その領域の面積に比例するはずなので、ランダムな点が円内に入る確率が円の面積と正方形の面積の比率に等しくなるはずです。
正方形の中に点が打たれる確率は $1$ です。
円の中に点が打たれる確率を $x$ とすると、
\begin{align*}
l^2 : \frac{l^2}{4} \pi &= 1 : x \\
\frac{l^2}{4} \pi &= l^2 x \\
\pi &= 4 x
\end{align*}
が成り立ちます。
そして、$x$ は円内に点が打たれる確率なので、正方形の中に打った点の個数で、円内に入った点の個数を割れば求めることができます。
これにより、円周率を確率的に求めることができます。
これを Python で実装すると以下のようなコードになります。円の中に入ったかどうかは円の方程式を考えれば判定できます。
import random
def estimate_pi(num_samples):
points_inside_circle = 0
total_points_attempted = 0
for _ in range(num_samples):
x = random.uniform(0, 1)
y = random.uniform(0, 1)
distance = x**2 + y**2
is_inside_circle = distance <= 1
if is_inside_circle:
points_inside_circle += 1
total_points_attempted += 1
pi_estimate = 4 * (points_inside_circle / total_points_attempted)
return pi_estimate
# 例: 100000 回サンプリングして円周率を推定
result = estimate_pi(100000)
print("推定された円周率:", result)
これを実行するとある程度近い値が出ます。これを CSS で実装すればよいのですが、いくつか問題があります。
CSS には乱数を得るための関数がないどころか、変数の状態を再評価する機能はありません。
しかし、それを可能にする CSS トリックがあります。The CPU Hack です。
The CPU Hack
詳しい仕組みは The CPU Hack の元記事を参照してください。
簡単に説明すると、継続的なデータの解析と、状態を再評価する機能を解除する CSS のトリックです。
アニメーションの仕様を用いてフレーム数のカウントなどができます。
以下に The CPU Hack でフレーム数をカウントするデモを示します。ホバーするとフレーム数がカウントアップされます。
See the Pen Untitled by Ryoga.exe (@Ryoga-exe) on CodePen.
このような表現が CSS のみでできます。
このデモにおける The CPU Hack の本質部分のコードは以下の部分です。
body {
animation: hoist 1ms infinite, capture 1ms infinite;
animation-play-state: paused, paused;
--frame-input: var(--frame-hoist, 0);
--frame-count: calc(var(--frame-input) + 1);
}
@keyframes hoist {
0%, 100% {
--frame-hoist: var(--frame-captured, 0);
}
}
@keyframes capture {
0%, 100% {
--frame-captured: var(--frame-count);
}
}
.cpu {
position: relative; list-style: none;
}
.cpu > * {
position: absolute;
inset: 0px;
width: 0px;
}
.cpu > .phase-0 {
width: 100%;
}
.cpu > .phase-0:hover + .phase-1 {
width: 100%;
}
.cpu > .phase-1:hover + .phase-2 {
width: 100%;
}
.cpu > .phase-2:hover + .phase-3 {
width: 100%;
}
CSS だけで疑似乱数列を生成 (Xorshift)
前述した通り CSS に乱数を得るための関数はありません。w3c の csswg-drafts の Issue に提案として上がってはいますが入る望みは現状低そうです。また、mozilla の standards-positions の Issue にも上がっていましたが、mozilla の見解としては random 関数の追加に否定的です。
いずれにせよ無いのでそれっぽいのを実装することにします。
今回は比較的実装が容易かつシンプルな疑似乱数列生成法である Xorshift を採用しました。
しかし、ここでもまた問題があります。
CSS には Xorshift で必要な XOR やビットシフトといったビット演算がありません。そのため Xorshift を実装することは不可能そうです。
ですが、四則演算は可能です。そのためうまく四則演算だけを使ってビット演算を表現できないか考えます。
$A, B$ を 1 bit の変数とすると、以下が成り立ちます。
| $A$ | $B$ | $A \mathbin{xor} B$ | $(A - B)$ | $(A - B)^2$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | -1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
よって上記の表より
$$
A \mathbin{xor} B = (A - B) \times (A - B)
$$
が言えます。
また、ビットシフトはビットごと個別に変数を持ち、一つづつずらしていくように更新すれば実装ができそうです。
例えば 変数 $A$ が上位ビットから順に $a_3, a_2, a_1, a_0$ であるとき、A << 2 は上位から順に $a_1, a_0, 0, 0$ と表せます。
そのため、それぞれのビットを別々の変数として持てば実装できます。
今回は Wikipedia の Xorshift に実装例として載っている xorshift32 を実装しました。
実装例として載っているコードを以下に一部引用します。
/* The state word must be initialized to non-zero */
uint32_t xorshift32(struct xorshift32_state *state)
{
/* Algorithm "xor" from p. 4 of Marsaglia, "Xorshift RNGs" */
uint32_t x = state->a;
x ^= x << 13;
x ^= x >> 17;
x ^= x << 5;
return state->a = x;
}
コードを読むと、32bit の変数が必要なのでそれに合わせて変数を 32 個持ちます。
コードは以下のようになります。
Xorshift の実装の一部
body {
animation: hoist 1ms infinite, capture 1ms infinite;
animation-play-state: paused, paused;
--p31-input: var(--p31-hoist, 1);
--p30-input: var(--p30-hoist, 0);
--p29-input: var(--p29-hoist, 0);
--p28-input: var(--p28-hoist, 1);
--p27-input: var(--p27-hoist, 0);
--p26-input: var(--p26-hoist, 0);
--p25-input: var(--p25-hoist, 1);
--p24-input: var(--p24-hoist, 0);
--p23-input: var(--p23-hoist, 1);
--p22-input: var(--p22-hoist, 1);
--p21-input: var(--p21-hoist, 0);
--p20-input: var(--p20-hoist, 1);
--p19-input: var(--p19-hoist, 0);
--p18-input: var(--p18-hoist, 1);
--p17-input: var(--p17-hoist, 1);
--p16-input: var(--p16-hoist, 0);
--p15-input: var(--p15-hoist, 1);
--p14-input: var(--p14-hoist, 0);
--p13-input: var(--p13-hoist, 0);
--p12-input: var(--p12-hoist, 0);
--p11-input: var(--p11-hoist, 1);
--p10-input: var(--p10-hoist, 1);
--p09-input: var(--p09-hoist, 0);
--p08-input: var(--p08-hoist, 0);
--p07-input: var(--p07-hoist, 1);
--p06-input: var(--p06-hoist, 0);
--p05-input: var(--p05-hoist, 1);
--p04-input: var(--p04-hoist, 0);
--p03-input: var(--p03-hoist, 0);
--p02-input: var(--p02-hoist, 0);
--p01-input: var(--p01-hoist, 1);
--p00-input: var(--p00-hoist, 0);
/*
q = (p_in xor (p_in << 13))
r = (q xor (q >> 17))
p = (r xor (r << 5))
*/
--q31: calc((var(--p31-input) - var(--p18-input)) * (var(--p31-input) - var(--p18-input)));
--q30: calc((var(--p30-input) - var(--p17-input)) * (var(--p30-input) - var(--p17-input)));
--q29: calc((var(--p29-input) - var(--p16-input)) * (var(--p29-input) - var(--p16-input)));
--q28: calc((var(--p28-input) - var(--p15-input)) * (var(--p28-input) - var(--p15-input)));
--q27: calc((var(--p27-input) - var(--p14-input)) * (var(--p27-input) - var(--p14-input)));
--q26: calc((var(--p26-input) - var(--p13-input)) * (var(--p26-input) - var(--p13-input)));
--q25: calc((var(--p25-input) - var(--p12-input)) * (var(--p25-input) - var(--p12-input)));
--q24: calc((var(--p24-input) - var(--p11-input)) * (var(--p24-input) - var(--p11-input)));
--q23: calc((var(--p23-input) - var(--p10-input)) * (var(--p23-input) - var(--p10-input)));
--q22: calc((var(--p22-input) - var(--p09-input)) * (var(--p22-input) - var(--p09-input)));
--q21: calc((var(--p21-input) - var(--p08-input)) * (var(--p21-input) - var(--p08-input)));
--q20: calc((var(--p20-input) - var(--p07-input)) * (var(--p20-input) - var(--p07-input)));
--q19: calc((var(--p19-input) - var(--p06-input)) * (var(--p19-input) - var(--p06-input)));
--q18: calc((var(--p18-input) - var(--p05-input)) * (var(--p18-input) - var(--p05-input)));
--q17: calc((var(--p17-input) - var(--p04-input)) * (var(--p17-input) - var(--p04-input)));
--q16: calc((var(--p16-input) - var(--p03-input)) * (var(--p16-input) - var(--p03-input)));
--q15: calc((var(--p15-input) - var(--p02-input)) * (var(--p15-input) - var(--p02-input)));
--q14: calc((var(--p14-input) - var(--p01-input)) * (var(--p14-input) - var(--p01-input)));
--q13: calc((var(--p13-input) - var(--p00-input)) * (var(--p13-input) - var(--p00-input)));
--q12: calc((var(--p12-input) - 0) * (var(--p12-input) - 0));
--q11: calc((var(--p11-input) - 0) * (var(--p11-input) - 0));
--q10: calc((var(--p10-input) - 0) * (var(--p10-input) - 0));
--q09: calc((var(--p09-input) - 0) * (var(--p09-input) - 0));
--q08: calc((var(--p08-input) - 0) * (var(--p08-input) - 0));
--q07: calc((var(--p07-input) - 0) * (var(--p07-input) - 0));
--q06: calc((var(--p06-input) - 0) * (var(--p06-input) - 0));
--q05: calc((var(--p05-input) - 0) * (var(--p05-input) - 0));
--q04: calc((var(--p04-input) - 0) * (var(--p04-input) - 0));
--q03: calc((var(--p03-input) - 0) * (var(--p03-input) - 0));
--q02: calc((var(--p02-input) - 0) * (var(--p02-input) - 0));
--q01: calc((var(--p01-input) - 0) * (var(--p01-input) - 0));
--q00: calc((var(--p00-input) - 0) * (var(--p00-input) - 0));
--r31: calc((var(--q31) - 0) * (var(--q31) - 0));
--r30: calc((var(--q30) - 0) * (var(--q30) - 0));
--r29: calc((var(--q29) - 0) * (var(--q29) - 0));
--r28: calc((var(--q28) - 0) * (var(--q28) - 0));
--r27: calc((var(--q27) - 0) * (var(--q27) - 0));
--r26: calc((var(--q26) - 0) * (var(--q26) - 0));
--r25: calc((var(--q25) - 0) * (var(--q25) - 0));
--r24: calc((var(--q24) - 0) * (var(--q24) - 0));
--r23: calc((var(--q23) - 0) * (var(--q23) - 0));
--r22: calc((var(--q22) - 0) * (var(--q22) - 0));
--r21: calc((var(--q21) - 0) * (var(--q21) - 0));
--r20: calc((var(--q20) - 0) * (var(--q20) - 0));
--r19: calc((var(--q19) - 0) * (var(--q19) - 0));
--r18: calc((var(--q18) - 0) * (var(--q18) - 0));
--r17: calc((var(--q17) - 0) * (var(--q17) - 0));
--r16: calc((var(--q16) - 0) * (var(--q16) - 0));
--r15: calc((var(--q15) - 0) * (var(--q15) - 0));
--r14: calc((var(--q14) - var(--q31)) * (var(--q14) - var(--q31)));
--r13: calc((var(--q13) - var(--q30)) * (var(--q13) - var(--q30)));
--r12: calc((var(--q12) - var(--q29)) * (var(--q12) - var(--q29)));
--r11: calc((var(--q11) - var(--q28)) * (var(--q11) - var(--q28)));
--r10: calc((var(--q10) - var(--q27)) * (var(--q10) - var(--q27)));
--r09: calc((var(--q09) - var(--q26)) * (var(--q09) - var(--q26)));
--r08: calc((var(--q08) - var(--q25)) * (var(--q08) - var(--q25)));
--r07: calc((var(--q07) - var(--q24)) * (var(--q07) - var(--q24)));
--r06: calc((var(--q06) - var(--q23)) * (var(--q06) - var(--q23)));
--r05: calc((var(--q05) - var(--q22)) * (var(--q05) - var(--q22)));
--r04: calc((var(--q04) - var(--q21)) * (var(--q04) - var(--q21)));
--r03: calc((var(--q03) - var(--q20)) * (var(--q03) - var(--q20)));
--r02: calc((var(--q02) - var(--q19)) * (var(--q02) - var(--q19)));
--r01: calc((var(--q01) - var(--q18)) * (var(--q01) - var(--q18)));
--r00: calc((var(--q00) - var(--q17)) * (var(--q00) - var(--q17)));
--p31: calc((var(--r31) - var(--r26)) * (var(--r31) - var(--r26)));
--p30: calc((var(--r30) - var(--r25)) * (var(--r30) - var(--r25)));
--p29: calc((var(--r29) - var(--r24)) * (var(--r29) - var(--r24)));
--p28: calc((var(--r28) - var(--r23)) * (var(--r28) - var(--r23)));
--p27: calc((var(--r27) - var(--r22)) * (var(--r27) - var(--r22)));
--p26: calc((var(--r26) - var(--r21)) * (var(--r26) - var(--r21)));
--p25: calc((var(--r25) - var(--r20)) * (var(--r25) - var(--r20)));
--p24: calc((var(--r24) - var(--r19)) * (var(--r24) - var(--r19)));
--p23: calc((var(--r23) - var(--r18)) * (var(--r23) - var(--r18)));
--p22: calc((var(--r22) - var(--r17)) * (var(--r22) - var(--r17)));
--p21: calc((var(--r21) - var(--r16)) * (var(--r21) - var(--r16)));
--p20: calc((var(--r20) - var(--r15)) * (var(--r20) - var(--r15)));
--p19: calc((var(--r19) - var(--r14)) * (var(--r19) - var(--r14)));
--p18: calc((var(--r18) - var(--r13)) * (var(--r18) - var(--r13)));
--p17: calc((var(--r17) - var(--r12)) * (var(--r17) - var(--r12)));
--p16: calc((var(--r16) - var(--r11)) * (var(--r16) - var(--r11)));
--p15: calc((var(--r15) - var(--r10)) * (var(--r15) - var(--r10)));
--p14: calc((var(--r14) - var(--r09)) * (var(--r14) - var(--r09)));
--p13: calc((var(--r13) - var(--r08)) * (var(--r13) - var(--r08)));
--p12: calc((var(--r12) - var(--r07)) * (var(--r12) - var(--r07)));
--p11: calc((var(--r11) - var(--r06)) * (var(--r11) - var(--r06)));
--p10: calc((var(--r10) - var(--r05)) * (var(--r10) - var(--r05)));
--p09: calc((var(--r09) - var(--r04)) * (var(--r09) - var(--r04)));
--p08: calc((var(--r08) - var(--r03)) * (var(--r08) - var(--r03)));
--p07: calc((var(--r07) - var(--r02)) * (var(--r07) - var(--r02)));
--p06: calc((var(--r06) - var(--r01)) * (var(--r06) - var(--r01)));
--p05: calc((var(--r05) - var(--r00)) * (var(--r05) - var(--r00)));
--p04: calc((var(--r04) - 0) * (var(--r04) - 0));
--p03: calc((var(--r03) - 0) * (var(--r03) - 0));
--p02: calc((var(--r02) - 0) * (var(--r02) - 0));
--p01: calc((var(--r01) - 0) * (var(--r01) - 0));
--p00: calc((var(--r00) - 0) * (var(--r00) - 0));
}
次にこの 32 個のビットから数値を復元します。monte-carlo-pi.css では上位 16 ビットを x 座標に、下位ビットを y 座標に割り当てています。結局二進数なので 10 進数に直すような計算をすればよいです。10 進数にしたのち、範囲を $[0, 1]$ に収めるため、最大値の $65535$ で割っています。
body {
--x: calc(
(
var(--p31) * 32768 +
var(--p30) * 16384 +
var(--p29) * 8192 +
var(--p28) * 4096 +
var(--p27) * 2048 +
var(--p26) * 1024 +
var(--p25) * 512 +
var(--p24) * 256 +
var(--p23) * 128 +
var(--p22) * 64 +
var(--p21) * 32 +
var(--p20) * 16 +
var(--p19) * 8 +
var(--p18) * 4 +
var(--p17) * 2 +
var(--p16) * 1
) / 65535
);
--y: calc(
(
var(--p15) * 32768 +
var(--p14) * 16384 +
var(--p13) * 8192 +
var(--p12) * 4096 +
var(--p11) * 2048 +
var(--p10) * 1024 +
var(--p09) * 512 +
var(--p08) * 256 +
var(--p07) * 128 +
var(--p06) * 64 +
var(--p05) * 32 +
var(--p04) * 16 +
var(--p03) * 8 +
var(--p02) * 4 +
var(--p01) * 2 +
var(--p00) * 1
) / 65535
);
}
円の中に点が入ったかどうかを判定する
次に必要なのは円の中に入ったかどうかを判定する処理です。
つまり、点 $(x, y)$ が円内にあるとき変数 $c$ をインクリメントするといった処理をしたいわけです。
もちろん CSS には変数の状態に応じた条件分岐はできないため、工夫します。
「点 $(x, y)$ が円内にあるとき変数 $c$ をインクリメントする」は
「変数 $c$ に $f(x, y)$ を足す (ただし、関数 $f(x, y)$ は点 $(x, y)$ が円内にあるときは $1$ を、そうでないときは $0$ を返すような関数)」と書けそうです。
ではそんな $f(x, y)$ を考えてみます。
円の半径が $r$ でその中心が $(0, 0)$ のとき、点 $(x, y)$ がこの円の中に入っているかどうかは $x^2 + y^2 \leq r^2$ で表せます。つまり $f(x, y) = g(x^2 + y^2)$ (ただし $g(t)$ は $t$ が $r^2$ 以下であるとき $1$ を、そうでないときは $0$ を返すような関数) と表現できます。
CSS で表現できるのは四則演算や最も近い整数に丸める処理 (Round)、そして max, min, clamp といった処理です。この中で関数 $g(t)$ を表現してみます。
試行錯誤すると以下のようなものが見つかります。
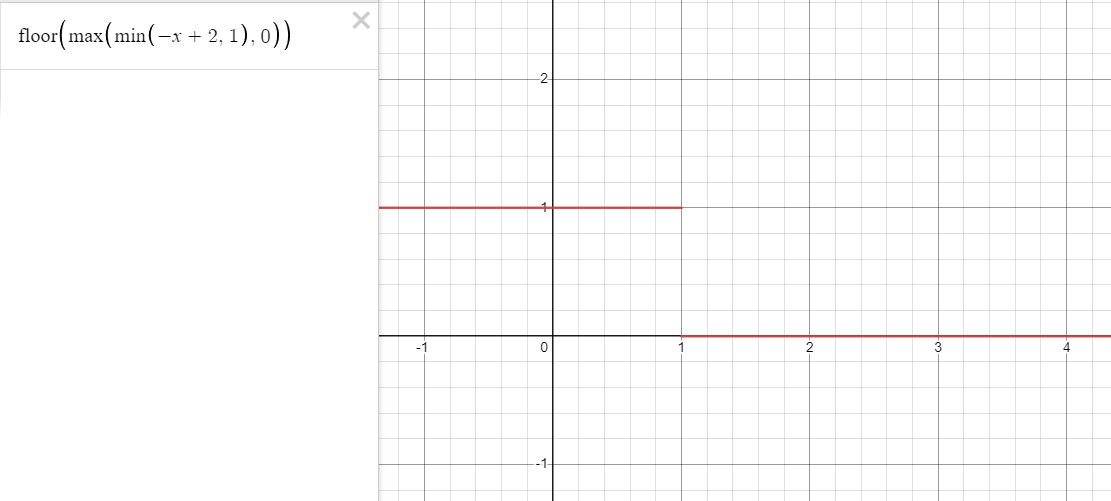
$$
\operatorname{floor}\left(\max\left(\min\left(-t\ +\ 2,\ 1\right),\ 0\right)\right)
$$
以下にこの関数のグラフを図示します。確かにこの関数が条件を満たすことが確認できます。
よって円の中に入ったかどうかの判定とそれのカウントは実装できそうです。
実際に monte-carlo-pi.css では以下のような実装をしています。
--is-inside: calc(clamp(0, -1 * (var(--x) * var(--x) + var(--y) * var(--y)) + 2, 1) - 0.5);
--inside-count: calc(var(--inside-count-input) + var(--is-inside));
--total-count: calc(var(--total-count-input) + 1);
...
@property --is-inside { syntax: "<integer>"; initial-value: 0; inherits: true; }
変数を表示する
ここまできたらあとは表示部分を作るだけです。
CSS 変数を表示するには CSS カウンターを使用します。
例えば変数 --hoge を表示したいとき、<div class="display-hoge"></div> のような div 要素を作り
.display-hoge::after {
counter-reset: hoge var(--hoge);
content: "--hoge: " counter(hoge);
}
のように書けば表示ができます。
しかし、MDN Web Docs で counter-reset について調べてみると、カウンターの初期値には <integer> 型、つまり整数型しか指定できません。
W3C の CSS Values and Units Module Level 4 でこれらの型について定義されています。これの 5.2.1. Computation and Combination of を見てみると、
Unless otherwise specified, the computed value of a specified is the specified abstract integer.
Interpolation of is defined as Vresult = round((1 - p) × VA + p × VB); that is, interpolation happens in the real number space as for s, and the result is converted to an by rounding to the nearest integer.
とあるので、実数型であるところの <number> を <integer> に変換すると、結果は最も近い整数に丸められることがわかります。
例えば、上記コードで --hoge が 2.5 であるとき、3 と表示されてしまいます。
今回は円周率を求める CSS を書くためこれでは困ります。小数点以下の値を正しく表示してほしいのですがこれではできません。
そのため、桁ごとに分けて表示することにしました。
以下、床関数を $\operatorname{floor}()$ で表します。(つまり $\operatorname{floor}(x) = \lfloor x \rfloor$ です)
また、最も近い整数に丸める関数を $\operatorname{round}$ で表します。
例えば $x = 1.23$ という $x$ があったとします。整数部分は $\operatorname{floor}(x)$ と表すことができ、また小数部分は $x - \operatorname{floor}(x)$ です。
これを $y$ とおくと、$y = 0.23$ ですから、$10y = 2.3$ です。$x$ を $10y$ で置き換えて同様のことをすると、$\operatorname{floor}(x) = 2$ となり少数第一位の桁を取り出すことができます。
これを繰り返すことによって少数点以下の各桁を得ることができます。
また、$\operatorname{floor}(x) = \operatorname{round}(x - 0.5)$ であるのでこの方法は CSS で表現が可能です。
例えば上記コードで --hoge が 1.234 のとき、小数点以下 3 桁を表示する CSS コードは以下のようになります。
.display-hoge::after {
--hoge: 1.234;
/* hoge の整数部分 (=1) */
--floor-hoge: calc(var(--hoge) - 0.5);
/* hoge の少数部分 * 10 (=2.34) */
--hoge-decimal00-in: calc((var(--hoge) - var(--floor-hoge)) * 10);
/* (hoge の少数部分 * 10) の整数部分 (=2) */
--hoge-decimal00: calc(var(--hoge-decimal00-in) - 0.5);
/* 以下同様に繰り返す */
--hoge-decimal01-in: calc((var(--hoge-decimal00-in) - var(--hoge-decimal00)) * 10);
--hoge-decimal01: calc(var(--hoge-decimal01-in) - 0.5);
--hoge-decimal02-in: calc((var(--hoge-decimal01-in) - var(--hoge-decimal01)) * 10);
--hoge-decimal02: calc(var(--hoge-decimal02-in) - 0.5);
counter-reset:
floor-hoge var(--floor-hoge)
hoge-decimal00 var(hoge-decimal00)
hoge-decimal01 var(hoge-decimal01)
hoge-decimal02 var(hoge-decimal02);
content:
"--hoge: "
counter(floor-hoge)
"."
counter(floor-decimal00)
counter(floor-decimal01)
counter(floor-decimal02);
}
/* floor を取るために @property を使って <integer> を指定し、丸め処理が行われるようにする */
@property --floor-hoge { syntax: "<integer>"; initial-value: 0; inherits: false; }
@property --hoge-decimal00 { syntax: "<integer>"; initial-value: 0; inherits: false; }
@property --hoge-decimal01 { syntax: "<integer>"; initial-value: 0; inherits: false; }
@property --hoge-decimal02 { syntax: "<integer>"; initial-value: 0; inherits: false; }
おわりに
これらを組み合わせれば CSS だけでモンテカルロ法を用いた円周率の近似が実装できます!
The CPU Hack を駆使すれば CSS だけでいろんな表現ができます!ぜひ皆さんも書いてみてください!