概要
UnityでComputeShaderに入門してみたので解説記事を書きます.
ComputeShaderで扱う題材として,ベクトル場を選びました.
粒子(Particle)を動かす際,ベクトル関数を用いて位置を更新する方法はよく見ます.
しかし今回は,ベクトル場そのものをあらかじめ別に定義して,その場から外力を受けるParticleという視点で実装しました.
最終的には以下のようものを作ります.

コード
ここにあげました!
目標
- ベクトル場について慣れる
- ComputeShaderでベクトル場を実装する
- ベクトル場を利用しParticleを動かしてみる
ベクトル場について
この記事は,ベクトル場についての簡単な概要説明に注力したいと思います.
(ベクトル場についてよく知らない人向けです.知識のある人は飛ばしてください.)
前提知識
- 座標空間
- スカラー,ベクトル
場とは
まず,ベクトル場の前に場という概念の説明をします.場とは物理を考える際に設定した舞台(環境)のことです.その舞台の各点で物理的な値が存在すると考えます.
身近な例として3次元空間のある点で気温が計測できるとするとその空間全体で"気温の場"を考えることができます.
上の例では空間上の値はスカラーなのでスカラー場と呼びます.
各点にベクトルを定義されているとするとその空間はベクトル場となります.
例えば,風の流れ(風速)を各点で計測すると,それは"風速ベクトル場"となります.
"場"と聞くと難しそうですが,意外と身近な概念だと思います.
場の数学的な表現
場がどういうものか分かったうえで簡単な例でベクトル場の数学的な表現を考えてみたいと思います.
相変わらず定義などの解説は避け,具体例をみて慣れていくことを目的とします.
まずは先ほどと同様,スカラー場を見ていきます.
数学的に場を表すと,座標$(x, y, z)$を指定して値が返ってくる関数と考えられます.
例えば
$$
f(x, y, z) = x+y+z
$$上の式は座標を指定すると$x+y+z$と値が返ってくる関数です.これを描画すると
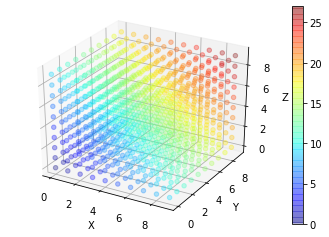
こんな感じになります.この図を眺めると$(x, y, z)$それぞれの値に比例して関数の値が大きくなることが直感的に分かります.
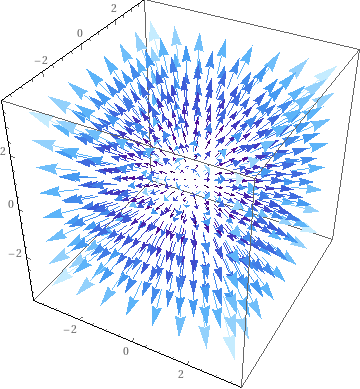
次にベクトル場です.例えば,
$$
\bf F \rm ( \it x, y, z \rm ) = \rm (\it x, y, z \rm )
$$スカラー場を表す関数との違いは座標を指定するとベクトルが返ってくることです.$\bf F$を描画すると
\bf{E} = \it \frac{q}{4\pi\epsilon_0 \|r^2\|}\frac{\bf r}{\|r\|} = a\bf F \\ \\
\bf r = \rm(\it x, y, z \rm)
と表されます. ベクトルにはノルム(ベクトルの長さの係数)が考えられるので,実際の$\bf E$は上の図と異なりますが値のベクトルが$\bf F$と平行であることを表しています.
ちゃんと勉強したい人は"ベクトル解析"と調べてみてください.
ComputeShaderによるベクトル場の実装
では,UnityのComputeShaderでベクトル場を実際に実装していきます.具体的には,座標を分割して,指定した座標におけるベクトルを計算することでベクトル場を表します.
実装に関してはUnityGraphicsProgrammingBook1のComputeShaderとBoidsシミュレーションの章を参考にしました.
ComputeShaderのC#側処理
$8\times8\times8$グリッドに分割したベクトル場を定義していきます.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using System.Runtime.InteropServices;
public class ComputeShaderScript : MonoBehaviour {
// VectorFieldの構造体
[System.Serializable]
struct VectorFieldData {
public Vector3 position;
public Vector3 direction;
public float dirScalar;
}
#region Grid
private int X_GRID = 8;
private int Y_GRID = 8;
private int Z_GRID = 8;
#endregion
#region ComputeShader & Buffer
public ComputeShader _cs;
// Direction格納したバッファ
public ComputeBuffer _VectorFieldDataBuffer;
#endregion
#region Accessors
// 基本データを格納したバッファを取得
public ComputeShader GetComputeShader()
{
return this._cs != null ? this._cs : null;
}
public ComputeBuffer GetVectorFieldDataBuffer()
{
return this._VectorFieldDataBuffer != null ? this._VectorFieldDataBuffer : null;
}
public int GetGridNum()
{
return X_GRID*Y_GRID*Z_GRID;
}
public Vector3 GetAreaCenter()
{
return new Vector3(0, 0, 0);
}
public Vector3 GetAreaSize()
{
return new Vector3(500f, 500f, 500f);
}
#endregion
/// <summary>
/// 破棄
/// </summary>
void OnDisable() {
if(_VectorFieldDataBuffer != null) {
_VectorFieldDataBuffer.Release();
_VectorFieldDataBuffer = null;
}
if(_ParticleDataBuffer != null) {
_ParticleDataBuffer.Release();
_ParticleDataBuffer = null;
}
}
/// <summary>
/// 初期化
/// </summary>
void Start() {
InitializeVectorFieldComputeBuffer();
}
/// <summary>
/// 更新処理
/// </summary>
void Update() {
ComputeShader cs = _cs;
int VectorFieldKernel = cs.FindKernel("VectorFieldMain");
cs.SetBuffer(VectorFieldKernel, "_VectorFieldDataBuffer", _VectorFieldDataBuffer);
cs.Dispatch(VectorFieldKernel, 1, 1, 1);
}
/// <summary>
/// Vectorfield computeBuffer Init
/// </summary>
void InitializeVectorFieldComputeBuffer() {
Vector3[] Position = new Vector3[X_GRID*Y_GRID*Z_GRID];
Vector3[] DirVector = new Vector3[X_GRID*Y_GRID*Z_GRID];
float[] DirScalar = new float[X_GRID*Y_GRID*Z_GRID];
for (int z = 0; z < Z_GRID; z++) {
for (int y = 0; y < Y_GRID; y++) {
for(int x = 0; x < X_GRID; x++) {
int i = z * (Y_GRID * X_GRID) + y * (X_GRID) + x;
Position[i] = new Vector3(x - (float)(X_GRID-1)/2, y - (float)(Y_GRID-1)/2, z - (float)(Z_GRID-1)/2);
DirVector[i] = new Vector3(Position[i].x, Position[i].y, Position[i].z);
DirScalar[i] = DirVector[i].magnitude;
}
}
}
// keep the size of VectorFieldData.
_VectorFieldDataBuffer = new ComputeBuffer(GetGridNum(), Marshal.SizeOf(typeof(VectorFieldData)));
// keep VectorFieldData Array.
VectorFieldData[] VFData = new VectorFieldData[_VectorFieldDataBuffer.count];
for (int i = 0; i < _VectorFieldDataBuffer.count; i++) {
VFData[i].position = Position[i];
VFData[i].direction = DirVector[i].normalized;
VFData[i].dirScalar = DirScalar[i];
}
_VectorFieldDataBuffer.SetData(VFData);
}
}
VectorFieldDataは座標positionとその座標におけるベクトルdirection,そしてdirectionベクトルのスカラーを持ちます.初期化の際,位置の指定方法には注意してください.ComputeBufferは1次元配列でデータを格納したいので,3重ループ内で1次元のindexを計算しています.
.compute
次にComputeShaderです.各座標におけるベクトルは計算せず.とりあえずスカラーだけ計算して書き込みます.
# pragma kernel VectorFieldMain
# define NUM_THREAD_X 8*8*8
# define NUM_THREAD_Y 1
# define NUM_THREAD_Z 1
# include "UnityCG.cginc"
struct VectorField {
float3 position;
float3 direction;
float dirScalar;
};
struct Particle {
float3 velocity;
float3 position;
float4 color;
float scale;
};
RWStructuredBuffer<VectorField> _VectorFieldDataBuffer;
[numthreads(NUM_THREAD_X, NUM_THREAD_Y, NUM_THREAD_Z)]
void VectorFieldMain (
uint3 id : SV_DispatchThreadID,
uint3 groupID: SV_GroupID,
uint3 groupThreadID: SV_GroupThreadID,
uint groupIndex: SV_GROUPINDEX
)
{
uint bufferIndex = id.x;
VectorField vf = _VectorFieldDataBuffer[bufferIndex];
_VectorFieldDataBuffer[bufferIndex] = vf;
}
レンダリング
ComputeShaderはGPUInstanceが相性良いようなのでこれを用いて描画します.
さまざまな方法があるようです.Graphics.DrawMeshInstancedIndirect
が使用方法の情報が多かったので採用しました.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
[RequireComponent(typeof(ComputeShaderScript))]
public class VectorFieldRenderer : MonoBehaviour {
#region Paremeters
// 描画するオブジェクトのスケール
public Vector3 ObjectScale = new Vector3(0.2f, 1.5f, 0.2f);
#endregion
#region Script References
// ComputeShaderスクリプトの参照
public ComputeShaderScript csScript;
#endregion
#region Built-in Resources
// 描画するメッシュの参照
public Mesh InstanceMesh;
// 描画のためのマテリアルの参照
public Material InstanceRenderMaterial;
#endregion
#region Private Variables
// GPUインスタンシングのための引数(ComputeBufferへの転送用)
// インスタンスあたりのインデックス数, インスタンス数,
// 開始インデックス位置, ベース頂点位置, インスタンスの開始位置
uint[] args = new uint[5] { 0, 0, 0, 0, 0 };
// GPUインスタンシングのための引数バッファ
ComputeBuffer argsBuffer;
#endregion
/// <summary>
/// 初期化
/// </summary>
void Start()
{
// 引数バッファを初期化
argsBuffer = new ComputeBuffer(1, args.Length * sizeof(uint),
ComputeBufferType.IndirectArguments);
}
/// <summary>
/// 更新処理
/// </summary>
void Update() {
// メッシュをインスタンシング
RenderInstancedMesh();
}
void OnDisable() {
// 引数バッファを解放
if (argsBuffer != null)
argsBuffer.Release();
argsBuffer = null;
}
void RenderInstancedMesh() {
// 描画用マテリアルがNull, または, computeShaderスクリプトがNull,
// またはGPUインスタンシングがサポートされていなければ, 処理をしない
if (InstanceRenderMaterial == null || csScript == null || !SystemInfo.supportsInstancing) {
return;
}
// 指定したメッシュのインデックス数を取得
uint numIndices = (InstanceMesh != null) ?
(uint)InstanceMesh.GetIndexCount(0) : 0;
args[0] = numIndices; // メッシュのインデックス数をセット
args[1] = (uint)csScript.GetGridNum(); // インスタンス数をセット
argsBuffer.SetData(args); // バッファにセット
// VectorFieldデータを格納したバッファをマテリアルにセット
InstanceRenderMaterial.SetBuffer("_VectorFieldDataBuffer",
csScript.GetVectorFieldDataBuffer());
// vectorFieldオブジェクトスケールをセット
InstanceRenderMaterial.SetVector("_ObjectScale", ObjectScale);
// 境界領域を定義
var bounds = new Bounds
(
csScript.GetAreaCenter(), // 中心
csScript.GetAreaSize() // サイズ
);
// メッシュをGPUインスタンシングして描画
Graphics.DrawMeshInstancedIndirect
(
InstanceMesh, // インスタンシングするメッシュ
0, // submeshのインデックス
InstanceRenderMaterial, // 描画を行うマテリアル
bounds, // 境界領域
argsBuffer // GPUインスタンシングのための引数のバッファ
);
}
}
あとはマテリアルに適応するshaderです.
Shader "myShader/VectorRenderer"
{
Properties
{
_Color ("Color", Color) = (1,1,1,1)
_MainTex ("Albedo (RGB)", 2D) = "white" {}
_Glossiness ("Smoothness", Range(0,1)) = 0.5
_Metallic ("Metallic", Range(0,1)) = 0.0
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 200
CGPROGRAM
#pragma surface surf Standard fullforwardshadows vertex:vert
#pragma instancing_options procedural:setup
#pragma target 3.0
struct Input
{
float2 uv_MainTex;
float4 color : COLOR;
};
// 構造体
struct VectorData
{
float3 position;
float3 direction;
float dirScalar;
};
#ifdef UNITY_PROCEDURAL_INSTANCING_ENABLED
// データの構造体バッファ
StructuredBuffer<VectorData> _VectorFieldDataBuffer;
#endif
float3 _ObjectScale;
sampler2D _MainTex; // テクスチャ
half _Glossiness; // 光沢
half _Metallic; // 金属特性
fixed4 _Color; // カラー
static const float PI = 3.14159265f;
float4 AngleAxis(float aAngle, float3 aAxis)
{
aAxis = normalize(aAxis);
aAxis *= sin(aAngle * 0.5);
return float4(aAxis.x, aAxis.y, aAxis.z, cos(aAngle * 0.5));
}
// calculate Quaternion between two vectors
float4 fromToRotationQuat(float3 aFrom, float3 aTo) {
float3 axis = cross(aFrom, aTo);
float angle = acos(dot(normalize(aFrom), normalize(aTo)));
return AngleAxis(angle, axis);
}
float4x4 quaternion_to_matrix(float4 quat)
{
float4x4 m = float4x4(float4(0, 0, 0, 0), float4(0, 0, 0, 0), float4(0, 0, 0, 0), float4(0, 0, 0, 0));
float x = quat.x, y = quat.y, z = quat.z, w = quat.w;
float x2 = x + x, y2 = y + y, z2 = z + z;
float xx = x * x2, xy = x * y2, xz = x * z2;
float yy = y * y2, yz = y * z2, zz = z * z2;
float wx = w * x2, wy = w * y2, wz = w * z2;
m[0][0] = 1.0 - (yy + zz);
m[0][1] = xy - wz;
m[0][2] = xz + wy;
m[1][0] = xy + wz;
m[1][1] = 1.0 - (xx + zz);
m[1][2] = yz - wx;
m[2][0] = xz - wy;
m[2][1] = yz + wx;
m[2][2] = 1.0 - (xx + yy);
m[3][3] = 1.0;
return m;
}
// 頂点シェーダ
void vert(inout appdata_full v)
{
#ifdef UNITY_PROCEDURAL_INSTANCING_ENABLED
// インスタンスIDからVectorFieldのデータを取得
VectorData VFData = _VectorFieldDataBuffer[unity_InstanceID];
float3 pos = VFData.position.xyz; // 位置を取得
float3 scl = _ObjectScale; // スケールを取得
// オブジェクト座標からワールド座標に変換する行列
float4x4 object2world = (float4x4)0;
scl.y *= VFData.dirScalar*0.5 + 0.25;
object2world._11_22_33_44 = float4(scl.xyz, 1.0);
// quaternion回転行列をかける
object2world = mul(quaternion_to_matrix(from_to_rotation(float3(0.0, 1.0, 0.0), VFData.direction)), object2world);
object2world._14_24_34 = pos.xyz;
// // 頂点を座標変換
v.vertex = mul(object2world, v.vertex);
// 法線を座標変換
v.normal = normalize(mul(object2world, v.normal));
#endif
}
void setup()
{
}
// サーフェスシェーダ
void surf (Input IN, inout SurfaceOutputStandard o)
{
fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color;
o.Albedo = c.rgb * IN.color;
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
// o.Emission = IN.color;
}
ENDCG
}
FallBack "Diffuse"
}
クォータニオン行列を使ってdirection方向に回転するようにしました.meshはy軸正の向きに定義したので2つのベクトル間の回転Quaternion.FromToRotationを参考に実装しました.
もう一つ注意が必要なのは,平行移動,回転を適応する順番です.それそれの方向に回転する矢印をグリッド上に配置したいので,回転行列かけてから平行移動してください.
描画すると以下のようになります.設定meshに円錐のmeshを自作して矢印のつもりで適応しました.

良さそうです.
ベクトル場から外力を受けるParticle
次に粒子を実装します.ベクトル場の実装とほとんど同じです.ParticleDataは速度velocity, 位置positionなどを構造体として持ちます.
重要な.computeのコードだけ記載します.
# pragma kernel VectorFieldMain
# pragma kernel ParticleMain
# define NUM_THREAD_X 8*8*8
# define NUM_THREAD_Y 1
# define NUM_THREAD_Z 1
# include "UnityCG.cginc"
struct VectorField {
float3 position;
float3 direction;
float dirScalar;
};
struct Particle {
float3 velocity;
float3 position;
float4 color;
float scale;
};
RWStructuredBuffer<VectorField> _VectorFieldDataBuffer;
RWStructuredBuffer<Particle> _ParticleDataBuffer;
float _DeltaTime;
///
/// void VectorFieldMain {
/// 上と同じです
/// }
///
[numthreads(NUM_THREAD_X,1,1)]
void ParticleMain (uint3 id : SV_DispatchThreadID)
{
int index = id.x;
Particle p = _ParticleDataBuffer[index];
for (int i = 0; i < NUM_THREAD_X; i++) {
VectorField vf = _VectorFieldDataBuffer[i];
float3 dir = p.position - vf.position;
float dist = sqrt(dot(dir, dir));
// 距離を計算して今いるグリッドを探査
if (dist > 0.0 && dist <= 1.0) {
p.velocity += vf.direction * vf.dirScalar * 0.1 * _DeltaTime;
p.position += p.velocity * _DeltaTime;
}
}
// ちなみに,ベクトル関数をそのまま用いると(p.positionが今回のベクトル関数に対応)
// p.velocity += p.position * 0.1 * _DeltaTime;
// p.position += p.velocity * _DeltaTime;
_ParticleDataBuffer[index] = p;
}
Particleの位置における先ほど定義した場の方向ベクトルから速度と位置を更新しています.
実際に見てみると以下のように,なかなかそれっぽい感じになりました.

応用
定義したVectorFieldのdirectionベクトルをcomputeShaderで計算しないと面白くありません.ノイズで動かしてみます.

いい感じです.
まとめ
今回実装した方法はParticleの位置に直接ベクトル関数を適応する方法に比べて精度は劣りますが,一度実装すれば,ベクトル場と粒子の運動を分離して考えられるのでより直感的に扱える気がします!
実装を通して個人的に考えたり,感じたことを列挙すると
-
精度
精度に関してはグリッドの分割数を細かくすることで解決できそうです. -
ComputeShaderの諸々のこと
まだcomputeShaderよくわかってないので,一次元のスレッドで実行しましたがスレッド,グループなどの概念にしっかり合わせて実装すれば実行速度の面においても十分有用そうであると感じました.
(ほんとはベクトル関数を用いた場合といろんなシチュエーションで比較したいんですけど...) -
その他の応用例
この記事では簡単な応用としてノイズをベクトルに反映しただけなので,わざわざベクトル場を分離したメリットはないように見えます.しかし,この方法ではベクトル場の1グリッド内でさまざまな物理量を定義して保存できるので格子法の流体プログラムに適応できそうだと思いました.(勉強不足なのでよくわかってないです.ごめんなさい🙇♂️)
これらは今後の課題とします.ちゃんとできたら追記したいとおもいます.
最後に
今回computeshaderの解説をほとんどせず,ベクトル場の概念の説明に比重をおきました.というのも,自分はまだ技術的なことを解説するほどよくわかっていません笑.webにある良い記事を読んだ方が良いと思います.
ベクトルのレンダリング部分でクォータニオンとか出てきましたが,それを除くとベクトル場を別に計算して粒子の運動に利用しただけです.
この記事を読んで,ベクトルやその他もろもろに対する抵抗が少しでも減ってくれたら嬉しいなぁと思ってます!
やってみたって感じの内容なのでまとまりのない文章だったと思いますが,ここまで読んでいただきありがとうございました.
内容に不備があった場合は優しく指摘していただけると幸いです.
参考
https://github.com/IndieVisualLab/UnityGraphicsProgrammingBook1
https://www.gakushuin.ac.jp/~881791/mathbook/
https://edom18.hateblo.jp/entry/2019/11/25/081232
https://edom18.hateblo.jp/entry/2018/01/18/081750