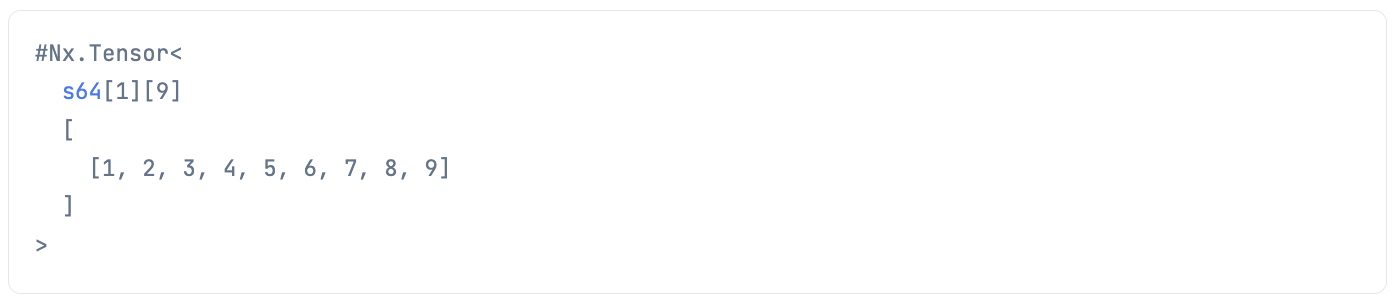Livebook で九九の表を作る（Enum版、Nx版）

はじめに

我が子が九九を暗唱しているので、私は九九を実装することにします

せっかくなので、 Enum でループするバージョンと Nx で行列演算するバージョンを2種類実装してみましょう

最終的に Kino.DataTable でいい感じに表示してみます

実装の全量はこちら

準備

Mix.install([
  {:nx, "~> 0.4"},
  {:kino, "~> 0.7"}
])

Enum

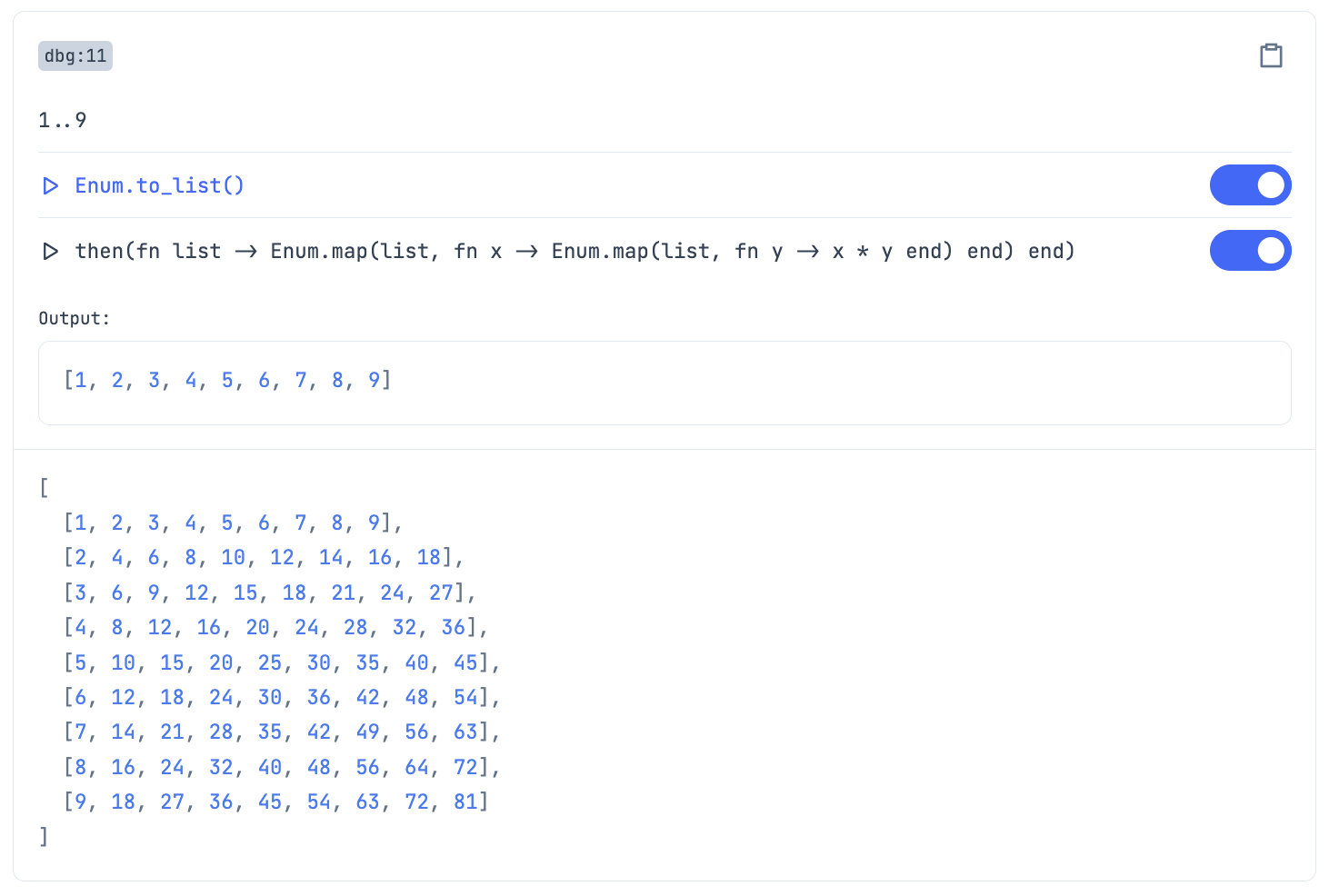
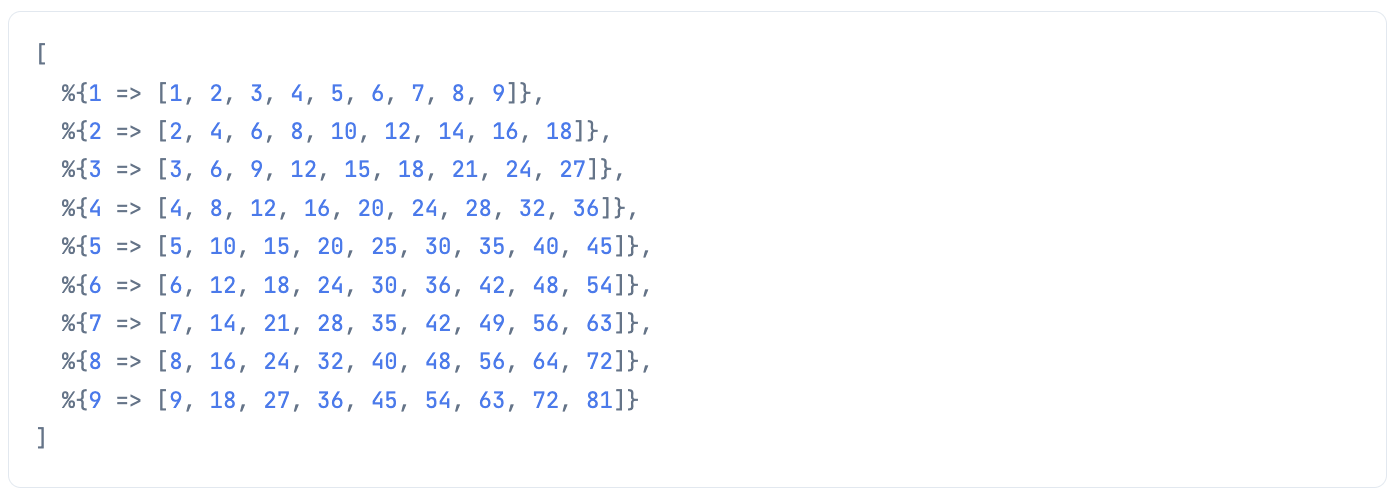
qq =
  1..9
  |> Enum.to_list()
  |> then(fn list ->
    Enum.map(list, fn x ->
      Enum.map(list, fn y ->
        x * y
      end)
    end)
  end)
  |> dbg()

特に解説するまでもないですが、 Enum.to_list(1..9) で 1 から 9 までの配列ができます

その配列を二重ループさせれば九九の出来上がりです

Nx

Nx でやった方がシンプルだよね、と思ったけど結構ゴチャゴチャしてしまった

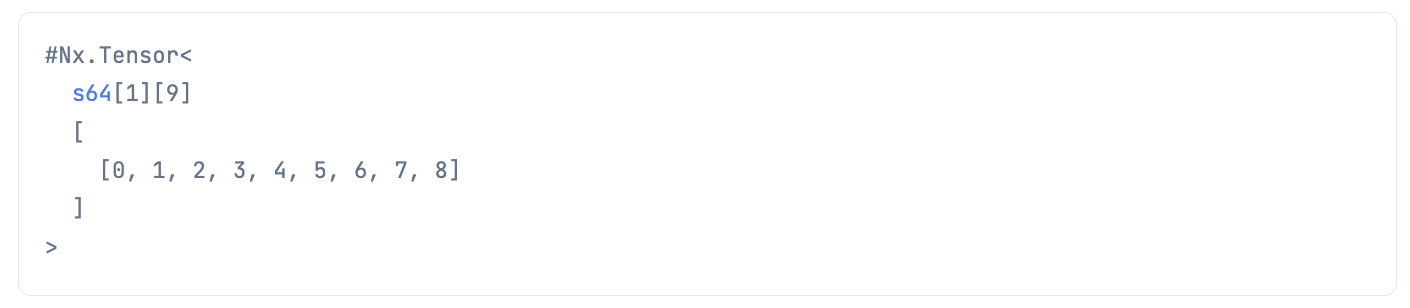
qq =
  {1, 9}
  |> Nx.iota()
  |> Nx.add(1)
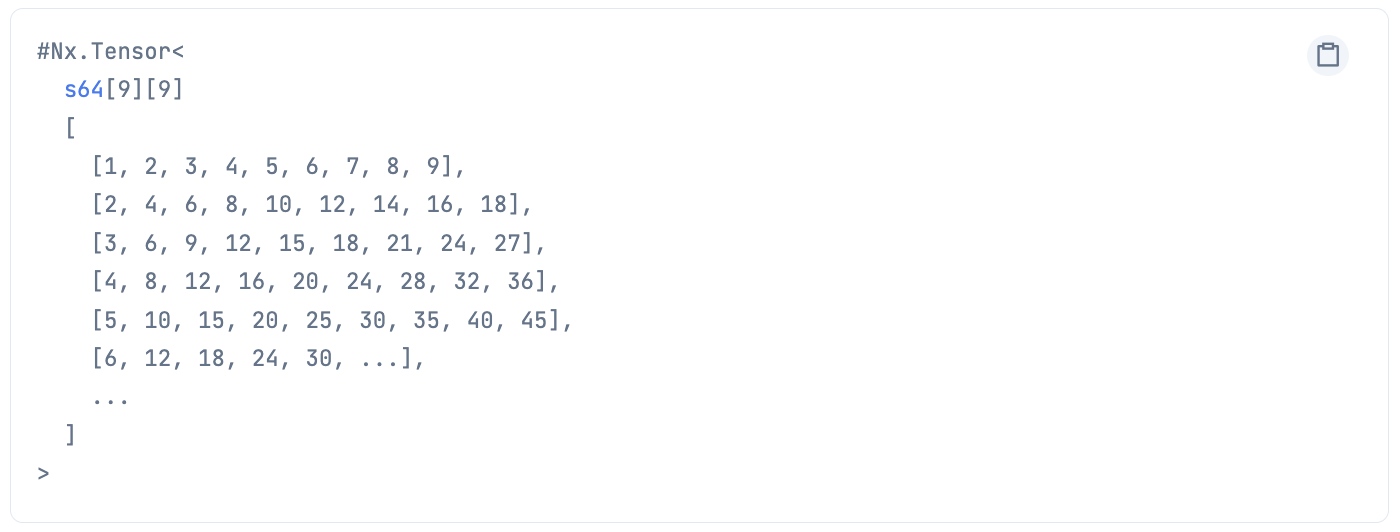
  |> then(&Nx.dot(Nx.transpose(&1), &1))
  |> Nx.to_flat_list()
  |> Enum.chunk_every(9)
  |> dbg()

まず Nx.iota({1, 9}) で 1 * 9 の2次元行列を作ります

これだと 0 から 8 になっているので Nx.add で全要素に 1 を足します

&Nx.dot(Nx.transpose(&1), &1) つまり、転置行列との内積によって一気に九九の計算をします

Nx.to_flat_list() で1次元配列にします

Enum.chunk_every(9) で 9 個毎に配列を分割すれば九九の出来上がりです

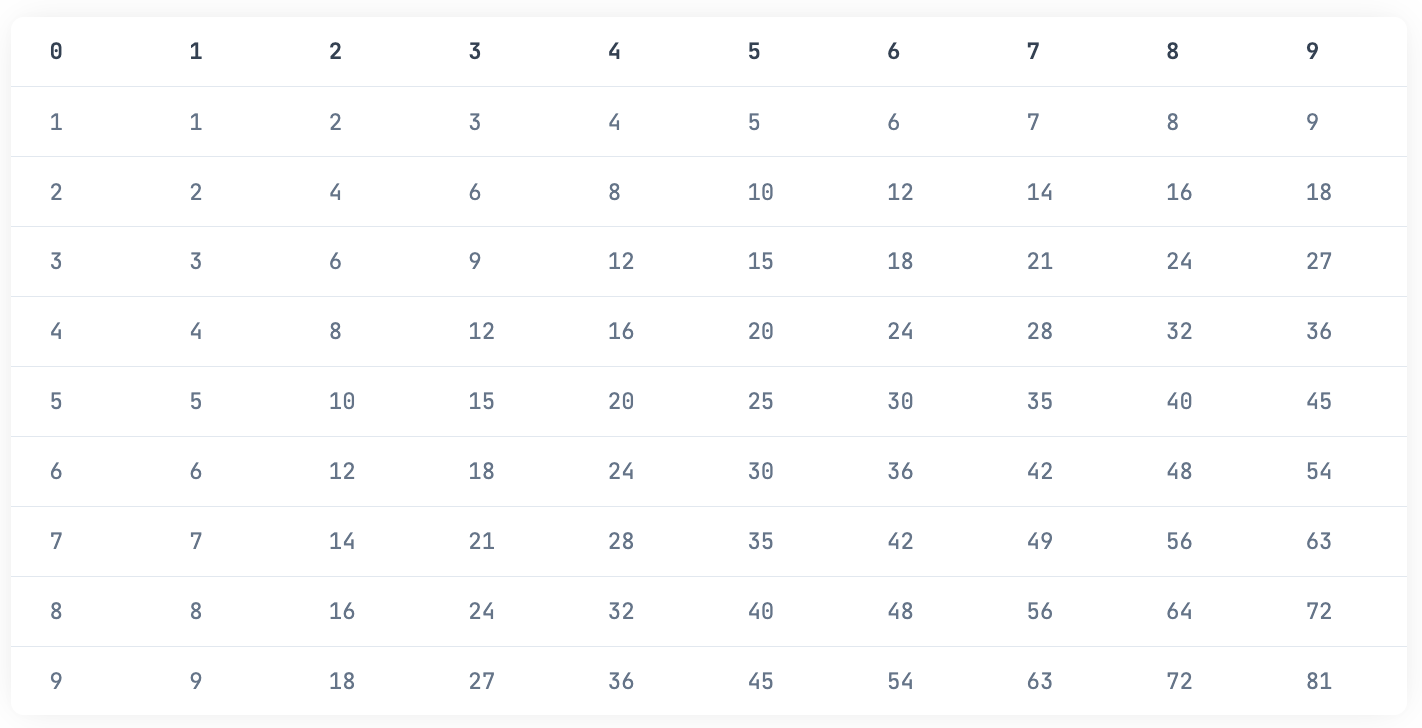
キレイに表示する

DataTable に表示しましょう

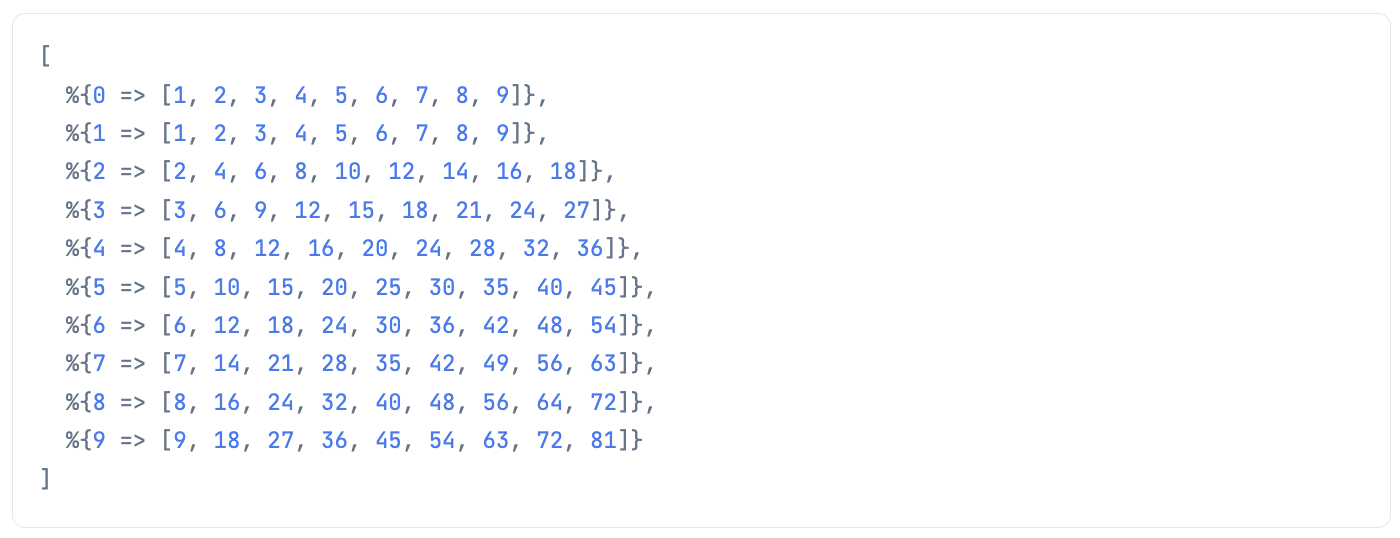
qq
|> Enum.map(&%{List.first(&1) => &1})
|> then(&[%{0 => Enum.at(&1, 0)[1]} | &1])
|> Enum.reduce(fn x, merged -> Map.merge(merged, x) end)
|> Kino.DataTable.new()
|> dbg()

Enum.map(&%{List.first(&1) => &1}) で、各段のマップにします

then(&[%{0 => Enum.at(&1, 0)[1]} | &1]) で、左端に何の段なのかを示す列を追加します

Enum.reduce(fn x, merged -> Map.merge(merged, x) end) により、マップの配列だったのを一つのマップに統合します

これを Kino.DataTable.new() に入れればキレイに表示できました

まとめ

ループ処理をできるだけ行列演算に変換するための訓練ですね