対象論文

3D Gaussian Splattingの概要

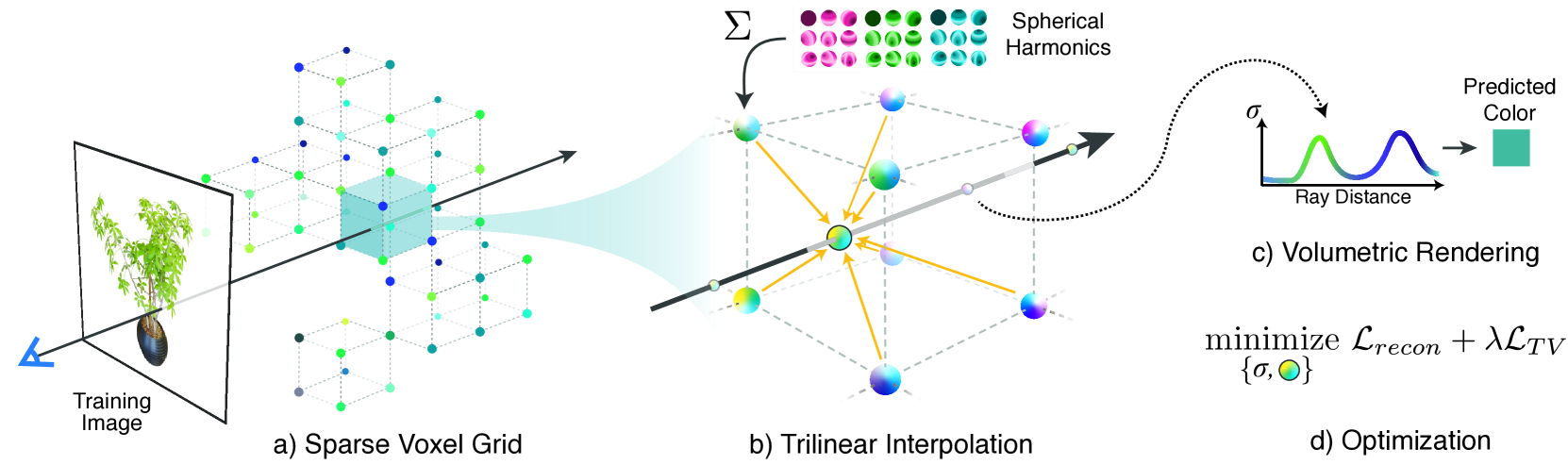
Luma AIでNeRFについで注目のコンピュータビジョンや医療画像処理など、様々な3D画像処理アプリケーションにおいて使用されるテクニックです。この手法は、データポイントを3D空間に「スプラット（splat）」することで、スパースなデータから連続的なボリュームデータを生成します。

0.忙しい方へのまとめ

NeRFは高い画質の3Dモデルングを生成することができます。

しかし、NeRFで高画質画像を生成するには訓練とレンダリングにコストのかかるニューラルネットワークを必要とします。

3D Gaussian Splattingではものなどの特定の対象物ではなく風景などに対して、1080pの解像度でリアルタイムの表示速度を実現しながら、状態最先端の視覚品質を達成するための3つのキーとなる要素を導入しています。

3Dガウス分布でシーンを表現：カメラで撮影した疎な点データからスタート。
最適化と密度制御：ガウス分布を調整してシーンを正確に再現し、計算量を削減。
高速レンダリングアルゴリズム：リアルタイムでのシーン描画を可能にする新技術。

1.論文解説

1.1 要約

高解像度（1080p）のリアルタイム（30 fps以上）の新視点合成を可能にする
カメラキャリブレーションから得られる疎な点を使用して、シーンを3Dガウシアンで表現。
連続体積放射フィールドの特性を維持しつつ、空間の無駄な計算を減らす。
3D位置、不透明度、異方性共分散、球面調和係数の最適化。
最適化プロセス中に3Dガウシアンを追加または時折削除することで、密度を適応的に制御。
GPU上で高速に動作するアルゴリズムを開発。
可視性を考慮しながら異方性スプラッティングを実現。
実際のシーンのリアルタイムレンダリングを可能にする。

コンピューターのディスプレーやプリンターにデータを出力する際、線や面などの図形要素で構成されるベクターグラフィックスをドットの集まりで表現するビットマップグラフィックスに変換した単一のガウス分布

[0]
これは次のパラメータで説明されます。

位置: どこにあるか (XYZ)
共分散: どのように拡張/スケールされるか (3x3 行列)
Color : 何色ですか (RGB)
アルファ: 透明度 (α)
これらを微分したりしてデータ描画します。

1.2 背景

[1]

メッシュや点ベースの3Dシーン表現の限界:

これらは明示的な表現であり、GPU/CUDAベースの高速ラスタライゼーションに適していますが、連続性や複雑なシーン構造を表現する能力に限界があります。

NeRFおよび関連手法の高コストとノイズ:

NeRFはMLPを用いることでボリュームレンダリングを可能にします。

ボクセルに格納された値を補間することによる連続表現に基づいて構築されています[2]

ハッシュ [3] グリッドまたはポイント [4]
これらはレンダリングで確率的サンプリングにはコストがかかりノイズもできる。

リアルタイムレンダリングの困難さ:

SOTA NeRF 手法のMip-NeRF360[5]は最大 48 時間のトレーニング時間が必要です。
高解像度のリアルタイム表示レートを達成する現行方法はありません。これは特に、高品質な新視点合成が必要なシーンでの問題となります。

品質と速度のトレードオフ:

高速なトレーニングを実現する最近の方法は、画像品質を犠牲にしています。

不完全なシーン再構築や“過剰再構築”の問題:

従来のシーン再構築とレンダリング方法では、再構築されていない領域や存在しないジオメトリを生成することがあります。

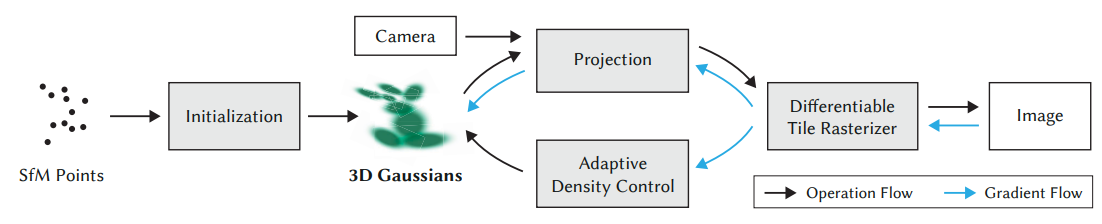
1.3モデルの構造

入力

静止シーンの多視点画像
各画像のカメラパラメータ(キャリブレーション情報)
スパースな3D点群(SfMの副産物として)

Structure From Motionからまばらな点群がせいせいされる。
位置(平均)、共分散行列、不透明度によって定義される3D ガウス分布のセットを作成（非常に柔軟な最適化体制が可能）(1.3.1)
シーンのコンパクトな表現のために異方性のあるボリュームスプラットを使用
方向に依存する表現には球面調和関数を使用
3Dガウスのパラメータとガウスの密度を制御することで、徐々にシーン表現を最適化
タイルベースのラスタライザにより、不透明度の重ね合わせと高速なソートを実現
逆伝播では重ね合わせた不透明度を記録することで、勾配を任意の数のガウスに伝えることが可能

1.3.1 微分可能な 3D ガウススプラッティング

ここでの目標は私たちの目標は、法線のない (SfM) 点のまばらなセットから開始して、高品質の新しいビュー合成を可能にするシーン表現を最適化することです。

まずはStructure from Motion で得られたカメラパラメータと、スパースな三次元点群が入力として利用

複数視点の画像と、それぞれのカメラパラメータ(内部パラメータ、外部パラメータ)
画像中の特徴点の対応関係
特徴点の三次元座標(スパースな点群)

このスパースな点群は、提案手法の初期化に利用されています。点群から3Dガウス関数を作成し、そのパラメータを最適化することで、密な三次元シーン表現を得ています。
ここでは以下のことをしています。

3Dガウス関数を位置、共分散行列、不透明度で定義
共分散行列をスケールと回転に分解して最適化しやすくする
カメラ空間に投影するための変換を導出
投影により3Dガウスを2Dスプラットとしてレンダリング
勾配を効率的に計算するために、明示的に導出

3Dガウス関数の定義

位置(平均)、共分散行列、不透明度によって表現
楕円体として視覚化可能

3Dガウス関数(3D Gaussian function)は、3次元空間におけるガウス分布を表す関数
各ガウス分布は世界空間における点（平均）に中心を置き、共分散行列Σによってその形状が決定されます。

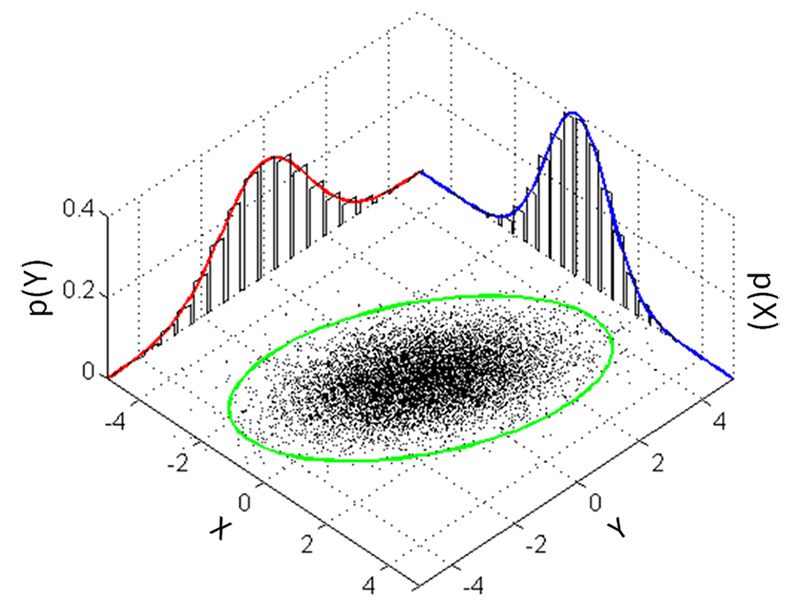
[6]

f(x) = \exp \left( -\frac{1}{2} x^\top \Sigma^{-1} x \right)

この式は、3D空間内の点群をモデル化する際に、それぞれの点がどのように空間的に分布しているかを表現するために使用されます。ガウス分布は、点群がどのように空間に広がっているかを示します。
この表現は、点群の空間的な分布を捉えるために使用されます。

2.2Dへの投影

カメラ座標系への変換
3Dガウスから2Dの分散行列を計算
2Dスプラットとして表現
3Dガウス関数をカメラ座標系に投影する時の共分散行列Σ'を最適化します。

\Sigma' = J W \Sigma W^T J^T

Σ : ワールド座標系での3Dガウス関数の共分散行列
W : ワールド座標系からカメラ座標系への変換行列
J : Wのアフィン近似のヤコビアン
Σ' : カメラ座標系での共分散行列

Wによってワールド座標系の3Dガウス関数をカメラ座標系に変換します。
その際の変換のヤコビアンJを用いて、変換後の共分散行列Σ'を計算しています。

この式は3D→2Dへの投影における共分散行列の変換方法を示しています。3Dガウス関数を2Dのスプラットとして投影するために必要な計算処理です。
3Dガウス関数を2Dのスプラット(Splat)に投影してレンダリングを行っています。

この投影計算により、3Dガウス関数を高速にレンダリング可能な2Dプリミティブに変換できています。

\Sigma = \text{RSS}^T R^T

Σをスケーリング行列Sと回転行列Rに分解する関係を示しています。

1.3.2OPTIMIZATION WITH ADAPTIVE DENSITY CONTROL OF 3D GAUSSIANS

最適化だけでは、ガウス関数の分布がシーンの局所的構造に適合しない場合がある
ある領域でガウス関数が密集しすぎたり、不足したりすることが起きうる
ガウス関数のサイズも一定だと表現力に限界がある
これらの問題は、最適化中に適応的に制御することで改善できる
密度とサイズをコントロールすることで、最適なガウス分布を導く
その結果、より精度の高いシーン表現が可能になる
また、適切な密度で表現できるのでメモリ効率やレンダリング速度向上にもつながる

以上の理由から、単純な最適化に更に適応的制御を加えることで、
高品質かつ効率的な3Dガウス関数の最適化が可能になる

最適化

3Dガウス関数のパラメータを初期化する
- 位置: SfMの点群位置
- スケール: 最近傍3点の平均距離
- 回転: 恒等回転
- 不透明度: 0.5
- SH係数: 0
現在のパラメータでレンダリングし、トレーニング画像との誤差を計算する
誤差に応じて、各パラメータの勾配を計算する
勾配 descentにより、各パラメータを更新する
- 位置: 減衰学習率適用
- 損失関数: L1 + DSSIM
2-4を繰り返し、パラメータを徐々に最適化する
一定期間ごとに、3Dガウス関数の密度制御（適応的にガウス関数の配置を最適化）を行う
条件を満たした場合、最適化処理を終了する

以上の流れで、3Dガウス関数のパラメータが最適化されていきます。
特に、スケールと回転の最適化により、共分散行列がシーンの幾何構造にフィットするようになります。

ガウス分布の適応制御

ガウス分布の制御なしに最適化だけで同等の結果を得ることは困難

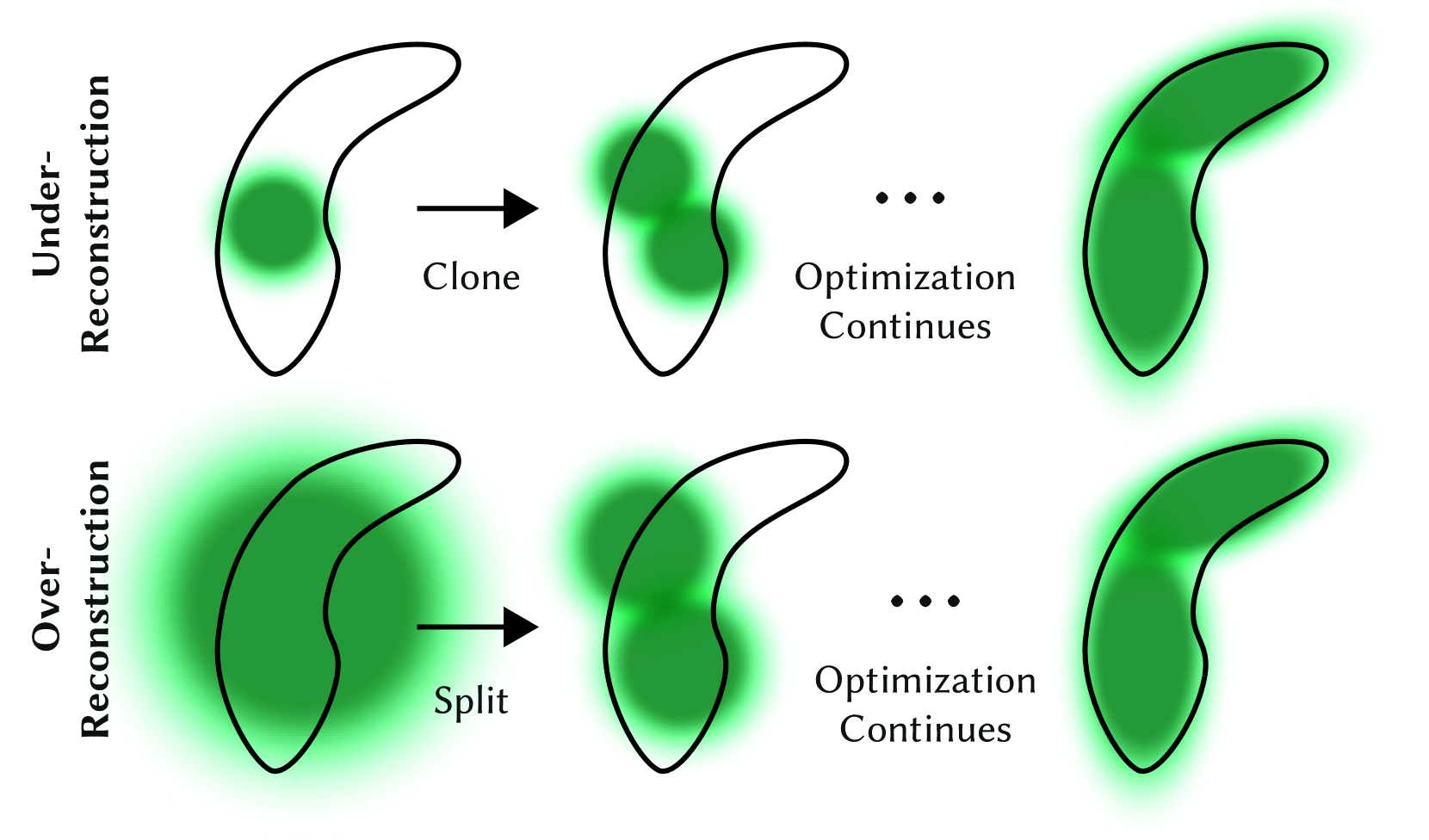
最適化処理の途中で、一定イテレーションごとに制御を行う。
各ガウス関数について、位置の勾配量を評価する。
勾配量が閾値より大きいガウス関数を制御の対象とする。
対象のガウス関数が小さい場合、クローンを作成して密度を上げる。
対象が大きい場合、2つに分割して密度を上げる。
不要なガウス関数(αが小さいなど)を削除する。
世界空間・ビュー空間でのサイズが大きすぎるものも削除。
最適化処理に戻る。

この流れで、ガウス関数の分布がシーンの構造に適応的に最適化されていきます。

特に、勾配ベースで制御対象を決定し、密度を適切にコントロールする点がポイントです。

1.3.3 ガウシアン用の高速微分可能ラスタライザ

スクリーンを16x16のタイルに分割して並列処理
3Dガウスをビュー空間の深度とタイルIDでソート
各タイル内でガウスを前から後ろにαブレンド
ピクセルのαが閾値に達したら処理を止める
後ろ向きパスでαの累積値を用いて効率的に勾配計算
ブレンドされるガウス数に制限がない

以上のように、タイルベースの処理とα累積値による勾配計算(確率的勾配降下法)がポイントです。

ガウス数の制限がないため、複雑なシーンでも学習可能です。アニソトロピックなガウスにも適用できます。

このラスタライザにより、3Dガウスの高速かつ正確な最適化とリアルタイムレンダリングが実現されています。

αブレンド(α blending)とは、コンピュータグラフィックスにおける画像合成の手法の一つです。複数の画像を重ね合わせる際に、それぞれの画像の透明度を表すα値を用いて合成する手法です。
具体的には、各画像のRGB値に加えてα値(0~1の実数)を持ち、α値に応じて画像を加重平均することで合成画像を生成します。
α値が高いほど不透明で、低いほど透明になります。
この論文では、3Dガウス関数を2Dスプラットに投影してレンダリングする際に、複数のスプラットをα値に基づいてブレンドしています。
前のスプラットのα値に応じて、後ろのスプラットの寄与を制御することで正しい合成結果を得ています。
つまり、本手法はαブレンドを利用した高速レンダリングを実現していると言えます。

1.4結果

以下スコアなどが出てきますので下記を参照してください。
https://qiita.com/toshi_machine/items/3ff0a09279a8e71c4e82

以前の方法との比較、および保持されたテストビューからの対応するグラウンドトゥルース画像を示します。

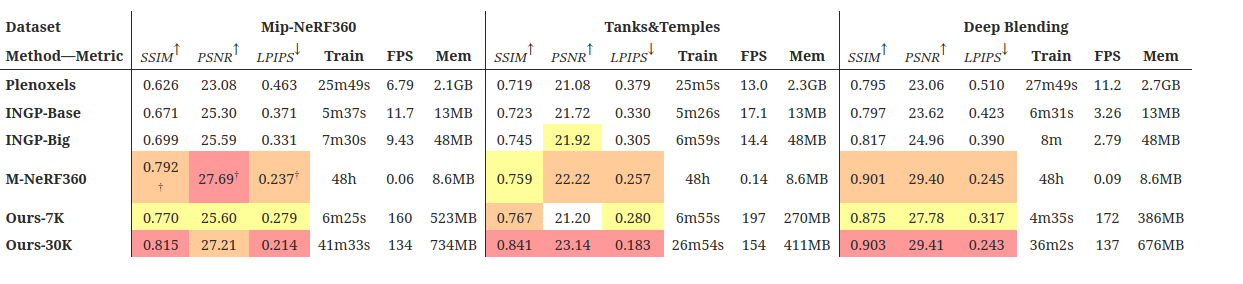
評価指標

7K と30K比較

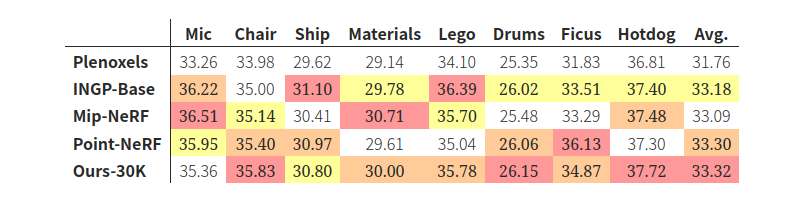
PSNR scores
PSNR Score

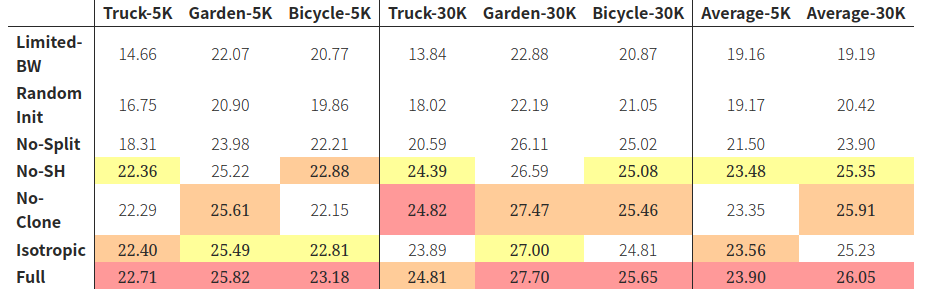
論文の結果によると、提案手法は従来の手法と比較して、トレーニング時間が短く、レンダリング品質が高いことが示されています。具体的には、トレーニング時間は最速の既存手法と同等で、レンダリング品質は最高の既存手法に匹敵することが実験で確認されたとのことです。